Sigo mirando esta foto y driving me crazy. ¿Cómo puede el círculo más pequeño viaje a la misma distancia cuando su circunferencia es de menos de la totalidad de la rueda?
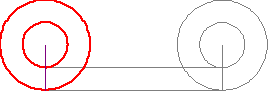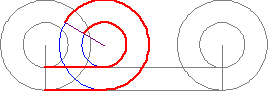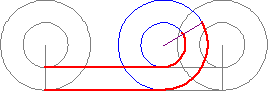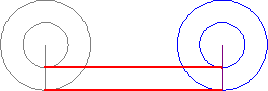
Sigo mirando esta foto y driving me crazy. ¿Cómo puede el círculo más pequeño viaje a la misma distancia cuando su circunferencia es de menos de la totalidad de la rueda?

Que imagen confunde las cosas, haciendo que parezca como si la línea roja se "desenrolla" desde el círculo como la toalla de papel se extrae de un rollo. Nuestros cerebros perciben, ya que es un ejemplo de la vida real.
Ambos círculos completar una sola vuelta, y ambos viajan a la misma distancia de la izquierda a la derecha. Si estas realmente eran rollos de toalla de papel, el más pequeño rollo tendría que girar más rápido (y por lo tanto, completa más de una revolución completa) con el fin de presentar la misma longitud de toalla de papel como el de mayor tirada. Alternativamente, si los dos rodillos se giran a la misma velocidad, el extremo libre de la tira de la toalla dejada por el más pequeño rollo también se movería hacia la derecha.
En resumen, la imagen es una especie de óptico/mental de la ilusión, y no va loco :)
Como el correo.James menciona, la cantidad de la línea roja trazada por el interior de la rueda es dos veces la circunferencia de la rueda interior. Así la impresión de que la rueda interior está rodando en la línea roja es una ilusión. En la actualidad, la rueda interior se desliza como sale de la línea roja. El deslizamiento es difícil de ver, ya que la única referencia fija que aparece en el interior de la rueda es su radio, que sigue a su rotación, y su radio sólo está cerca de la línea en la que la rueda está rodando en los extremos de la línea.
He aislado el interior de la rueda y se coloca una segunda rueda justo debajo de lo que en realidad sale en rojo y verde de la línea en una longitud adecuada para la longitud y forma. Viendo los dos juntos, hace que el deslizamiento sea más notoria.
${\hspace{4cm}}$
Si los dos círculos son fijos, entonces ellos estarán viajando a la misma diferencia, pero a diferentes velocidades.
De hecho, la relación de los radios es igual a la relación de velocidades de un punto sobre el círculo de viajarán.
Si se trató de repetir esto por poner dos diferentes tamaños de círculos en una pista y haciéndolos girar a salir a la misma distancia con la misma velocidad angular, te darás cuenta de que uno de los círculos se tiene que deslizar/deslizarse a lo largo de la pista con el fin de mantenerlos en el mismo ritmo.
Tiene dos cilíndrico ruedas giran sobre un eje que pasa por sus centros. Dibujar una línea vertical hacia el eje. En el punto de la intersección de la línea con las dos ruedas de lazo en cada punto de una bola de cuerda. Después de una revolución de la longitud de la cadena en cada rueda cilíndrica son diferentes y proporcional al radio de las ruedas.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.