Límite de Gamma integrales

Question

El siguiente parece a celebrar en las simulaciones numéricas, es cierto? $$\lim_{n\to \infty} \int_0^1 dx \frac{n! 2^{-n} n}{(n x)!(n-n x)!\sqrt{x(1-x)}}=2$$

Es una combinación de dos conocidos integrales

$$\lim_{n\to \infty} \int_0^1 dx \frac{n! 2^{-n} n}{(n x)!(n-n x)!}=1$$

$$\int_0^1 dx \frac{1}{\sqrt{x(1-x)}}=\pi$$

Primero sigue de asintótica de expansión de la Gamma y la segunda se realiza mediante sustitución trigonométrica

Edit: $x!$ es corto para $\Gamma(x+1)$.

Límite de convergencia es evidente para $n$ entre 10 y $10^6$, $\log_{10} n$ da casi un ajuste perfecto para el registro de desviación

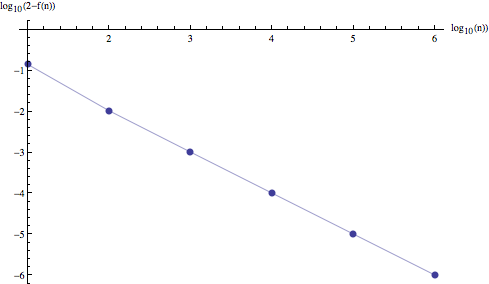
La motivación, la última integral es una instancia de "Volumen de Información", una estimación del número de estadísticamente distinguibles de las distribuciones en el modelo de Bernoulli, que se utiliza como una medida de la complejidad del modelo . Una de las principales molestias es que esta integral no existe para algunos de los modelos más populares, como la distribución geométrica de la familia. Tal vez podamos solucionar este problema, en lugar de estimar el número de la observación de las secuencias que se ajuste por algunos de distribución en el modelo? Esa es la primera integral.

Answer 1

Esto no es nada misterioso, es la continua analógica de $\Sigma 2^{-n} \binom{n}{k} = 1$ con factoriales interpolados por funciones Gamma, que varían bastante bien en la gama media , donde la suma se concentra y tiene aproximadamente la distribución Gaussiana, $k = n/2 + O(\sqrt{n})$.

La relación entre el discreto paso de la función y la interpolación continua es $1+O(1/n)$ en el rango medio (el uso de los primeros términos de Stirling asintótica de expansión para $\Gamma$).

El $1/\sqrt{x(1-x)}$ es irrelevante porque es, efectivamente, un factor constante $2 + O(1/n)$ en el rango medio.

La gama media tiene la anchura de menos de $n^{1/2 + \epsilon}$.

Así, la escritura de la integral en términos de $u = nx$,

$$I_n = \int_0^n \binom{n}{u} 2^{-n} du \frac {1} {\sqrt{x(1-x)}} \sim 2 \int_0^n \binom{n}{u} 2^{-n} du \sim 2$$

con un aditivo de error de $O(n^{\epsilon - 1/2})$. El $\epsilon$ puede ser una pequeña constante positiva o una infinitesimal dependiendo de cómo diseccionar la integral de en medio y colas (tenemos que elegir un corte para cada una de las $n$, de tal manera que la totalidad de la gama media está cubierto como $n \to \infty$; cualquier conjunto de opciones de probar la convergencia, pero la tasa de convergencia depende de las opciones).

Answer 2

Límite (e incluso de forma asintótica de la serie) de la integral puede ser calculada usando el método de Laplace y a Stirling aproximación. La solución se puede hacer en 5 pasos:
1. Demostrar, que la integral sobre la $[0,1/n]$ puede ser descuidado. Para ello, utilice Stirling aproximación para todos los factoriales con la excepción de $(nx)!$, que puede ser aproximada por una constante.
2. Demostrar, que la integral sobre la $[1/n,\delta]$ puede ser descuidado (por $\delta<1/2$). Para ello, utilice Stirling aproximación para todos los factoriales (nota, que $z!/(\sqrt{2 \pi z} (z/e)^z))$ está limitada en ambos lados por constantes positivas si $z>=1$).
3. Por medio de la simetría de saber, que su límite es igual a $\lim_{n\to\infty}\int_{\delta}^{1-\delta}dx(\dots)$.
4. El uso de Stirling aproximación a la aproximación de factoriales. Usted obtendrá los siguientes:
$$\int_{\delta}^{1-\delta}dx\frac{n!2^{-n}n}{(xn)!(n-xn)!\sqrt{x(1-x)}}=(1+O(n^{-1}))\sqrt{\frac{n}{2\pi}}\cdot$$ $$\int_{\delta}^{1-\delta} x^{-1}(1-x)^{-1}exp\bigl(-n(x\ln x+(1-x)\ln(1-x)+\ln 2)\bigr)dx$$
5. Aplicar el método de Laplace a la última integral y de llegar es asintótica.

Answer 3

$\newcommand{\ángulos}[1]{\left\langle #1 \right\rangle}% \newcommand{\llaves}[1]{\left\lbrace #1 \right\rbrace}% \newcommand{\bracks}[1]{\left\lbrack #1 \right\rbrack}% \newcommand{\dd}{{\rm d}}% \newcommand{\ds}[1]{\displaystyle{#1}}% \newcommand{\expo}[1]{{\rm e}^{#1}}% \newcommand{\equalby}[1]{{#1 \cima {= \cima \vphantom{\enorme}}}}% \newcommand{\ic}{{\rm i}}% \newcommand{\imp}{\Longrightarrow}% \newcommand{\pars}[1]{\left( #1 \right)}% \newcommand{\pp}{{\cal P}}% \newcommand{\ul}[1]{\underline{#1}}% \newcommand{\verts}[1]{\left\vert #1 \right\vert}$

$\ds{% {\cal F}_{n} \equiv \int_{0}^{1} {\dd x \más \pars{nx}!\,\pars{n - nx}!\,\sqrt{x\,\pars{1 - x\,}\,}}\,, \qquad \lim_{n \to \infty}\bracks{{\pars{n + 1}! \más de 2^{n}}\,{\cal F}_{n}} \ \equalby{?} \ 2}$

$\tt\large Hint$:

\begin{align} \pars{nx}!\pars{n - nx}! &\approx \bracks{\sqrt{2\pi\,}\,\pars{nx}^{nx + 1/2}\expo{-nx}} \bracks{\sqrt{2\pi\,}\,\pars{n - nx}^{n - nx + 1/2}\expo{-\pars{n - nx}}} \\[3mm]&= 2\pi\,\expo{-n}\bracks{n^{nx + 1/2}\,x^{nx + 1/2}} \bracks{n^{n - nx + 1/2}\pars{1 - x}^{n - nx + 1/2}} \\[3mm]&= 2\pi\,\expo{-n}\,n^{n + 1}x^{nx + 1/2}\pars{1 - x}^{n - nx + 1/2} \\[3mm]&= \sqrt{2\pi\,}\,{\rm e}\,{n^{n + 1} \over \pars{n + 1}^{n + 3/2}}\bracks{% \sqrt{2\pi\,}\,\pars{n +1}^{n + 3/2}\expo{-\pars{n + 1}}} x^{nx + 1/2}\pars{1 - x}^{n - nx + 1/2} \\[3mm]&\approx \sqrt{2\pi\,}\,{\rm e}\,{n^{-1/2} \over \pars{1 + 1/n}^{n + 3/2}}\,\pars{n + 1}!\; x^{nx + 1/2}\pars{1 - x}^{n - nx + 1/2} \\[3mm]&\approx \sqrt{2\pi\,}\,n^{-1/2}\pars{n + 1}!\; x^{nx + 1/2}\pars{1 - x}^{n - nx + 1/2} \end{align}

$$ \pars{nx}!\pars{n - nx}! \aprox {\sqrt{2\pi\,} \over n^{1/2}}\, \pars{n + 1}!\;x^{nx + 1/2}\pars{1 - x}^{n - nx + 1/2} $$

\begin{align} {\cal F}_{n} &\approx {n^{1/2} \over \sqrt{2\pi\,}\,\pars{n + 1}!} \int_{0}^{1}x^{-1 - nx}\pars{1 - x}^{-1 - n + nx}\,\dd x \end{align}