¿Cambia la presión de los neumáticos del coche con el peso de la carga del coche?

Question

¿La presión de los neumáticos medida por un medidor en la presión del neumático cambia con la carga? (No me interesa la presión producida por los neumáticos del coche sobre la carretera).

Normalmente, la especificación del coche dice "inflar a 220 kPa carga normal, 300 kPa carga completa". ¿Significa esto que la presión medida debe ser de 300 kPa solo después de que el coche haya sido cargado, o se puede inflar los neumáticos a los 300 kPa recomendados mientras está vacío y luego cargar el coche con 500 kg sin necesidad de volver a medir la presión?

Básicamente, se pueden encontrar ambas respuestas al investigar en los foros no relacionados con la física en internet:

• Una explicación dice que la llanta se comprimirá bajo una carga mayor, lo que hará que el volumen dentro de la llanta sea más pequeño, por lo tanto, la presión será mayor. También afirma que esta es la razón por la cual la placa de especificaciones en el coche tiene dos valores: simplemente debes esperar medir una presión más alta en los neumáticos mientras el coche está cargado.

• También hay explicaciones que indican que el aire no escapa de la llanta, por lo tanto, la cantidad de aire dentro de la llanta es constante y la presión medida en los neumáticos es constante incluso si el coche está cargado (y según las observaciones, los neumáticos normalmente se comprimen cuando el coche está cargado). Esto significaría que se necesita poner más aire en los neumáticos cuando el coche está cargado para garantizar una presión más alta.

Para un lego, ambas suenan factibles.

¿Está una de las explicaciones simplificando basándose en suposiciones de carga normal? (es decir, la presión de los neumáticos no cambia si el coche está cargado con un máximo de 1000 kg, ¿pero cambiaría si se pusiera una carga enorme en el coche?)

¿Dónde está la verdad?

Answer 1

TL;DR: La carga no aumenta significativamente la presión en el neumático, pero no inflar más el neumático aumentará la fricción. Esto calentará el neumático. La presión correcta garantiza el área de contacto correcta, evitando el desgaste del neumático y manteniendo la fricción de rodadura baja.

Respuesta completa: Voy a usar matemáticas simples, números redondos (sin calculadora): automóvil de 1000 kilos, 4 neumáticos, presión de 2.2 bares. El área de contacto para cada neumático es aproximadamente $250 / 2.2 = 110 ~\rm{cm^2}$. Con el neumático de 15 cm de ancho, la superficie de contacto es de 6 cm de largo.

Ahora "carguemos" el automóvil con un 50% más de peso (500 kg). El área de contacto adicional necesaria es de $55~\rm{cm}^2$ por neumático. Si asumimos que los costados del neumático no se deforman, la longitud de contacto aumenta a 9 cm.

El cambio en el volumen debido a este aplanamiento adicional del neumático es bastante pequeño. Observando el diagrama a continuación, puedes calcular el cambio de volumen (asumiendo que toda la deformación ocurre en este plano)

El volumen del aire en el tubo no deformado:

$$\begin{align}V &= \pi (r_o^2 - r_i^2) w\\ V &= \rm{volumen}\\ w &= \rm{ancho\ del\ neumático}\end{align}$$ El ángulo subtendido por la región plana: $$\theta = 2\sin^{-1}(\frac{L}{2r_o})$$ cuando $L<

El área de la región aplanada es $$A_{plano}=\frac12r_o^2\theta - \frac{L}{2} r_o \cos\frac{\theta}{2}$$

Aproximación de ángulo pequeño:

$$\begin{align} A_{plano}&=\frac12r_oL(1-(1-\left(\frac{L}{2r_o}\right)^2))\\ &=\frac{L^3}{8r_o}\end{align}$$

Para un ancho constante $W$ del neumático, el volumen aplanado es, por supuesto, $Aw$.

Si asumimos de primer orden que la fricción es proporcional al volumen que se está distorsionando, puedes ver que un neumático ligeramente aplanado (con mayor área de contacto) afectará significativamente el consumo de combustible.

¿Qué tan grande es el efecto? Con los números que utilicé anteriormente, el cambio de volumen fraccional es solo 0,03% (para $r_i = 30~\rm{cm}, r_o = 40~\rm{cm}, w = 15~\rm{cm}$). Eso significa que la presión no aumentará debido a la deformación del neumático / la masa adicional.

Y eso a su vez significa que la razón para inflar más el neumático es precisamente para evitar el aumento del área de contacto, lo que llevaría a una mayor fricción y posiblemente a una temperatura más alta.

Como señaló @Tom, bajo carga, el lateral de un neumático también se deformará, y esta deformación causará un desgaste adicional en el neumático. Esta es otra razón por la cual la presión de los neumáticos debe ajustarse a la carga.

Observa que hay un bucle de retroalimentación: si el neumático está insuflado y cargado pesadamente, se calentará lo que aumentará ligeramente la presión. Pero es mejor comenzar con un poco más de aire en él...

Answer 2

Los datos que proporcionan los fabricantes suponen que la presión de los neumáticos se ajusta con los neumáticos fríos (temperatura ambiente) antes de cargarlos. Aunque el pequeño error introducido al hacer ajustes después de cargarlos no será significativo, la diferencia entre los neumáticos fríos y calientes es mayor.

La presión recomendada es mayor para un automóvil 'plenamente cargado'. Por eso, una llanta de repuesto debe mantenerse a mayor presión.

Estoy buscando la verdad ultima para esta pregunta y aunque tu respuesta proporciona un muy buen consejo práctico, la respuesta parece bastante vaga y aún menciona un "pequeño error". ¿Podrías por favor aclarar en términos de física y proporcionar una respuesta sobre si la presión de los neumáticos aumenta bajo carga o no, respaldado por la física (incluso si la diferencia sería insignificante)?

No sé si hay una medida concreta específica que responda a tu pregunta, mi respuesta implicaba una deducción lógica: si la presión aumentara de manera no despreciable, los fabricantes no recomendarían aumentar la presión.

Además, es imposible dar una respuesta general que sea válida para todos los neumáticos. Me temo que la verdad última no está allí porque no puede existir. El aumento de presión sólo se produce si el neumático es deformable, y si lo es, entonces debes tener en cuenta si la diferencia de volumen es significativa. Si un objeto es esférico o cilíndrico, cualquier deformación automáticamente producirá una disminución de volumen. Ningún neumático es así.

http://www.sturgeontire.com/images/glossary/crosssection.jpg

Dado que las paredes laterales nunca son circulares, es incluso posible que la presión vertical sobre la banda de rodadura produzca una deformación de la pared lateral que le dé una forma más circular, aumentando el volumen (de manera insignificante).

La respuesta física solo puede ser teórica y es bastante obvia y simple: si hay una carga que produce una deformación que produce una disminución de volumen en la misma proporción, la presión aumenta proporcionalmente a esto.

... simplemente deberías esperar medir una presión más alta en los neumáticos mientras el auto esté cargado.

Probablemente lo que escribiste en la 'primera explicación' arriba es lo que te desconcertó y te confundió, ¿verdad?: de todas maneras, debes inflar tu neumático hasta la presión recomendada más alta antes de cargar el auto, (y no estoy seguro si debes esperar medir una presión más alta cuando el auto esté cargado). Esto es porque una presión más alta evita la deformación. Eso es todo lo que puedo deducir.

Sugieres que en la práctica se debe observar la segunda explicación e inflar los neumáticos al esperar carga, pero no encontré esto en el manual de mi auto. ¿Tienes alguna referencia?

Probablemente lo dan por sentado, pero realmente no importa si lo mides antes o después de cargar el auto: la presión a carga completa _debe y será de 300kPa_NSCEP "los laboratorios de prueba hacen la verificación de presión antes de cargar el neumático". Cualquier empleado de una estación de servicio lo confirmará.

Answer 3

La pregunta: ¿La presión dentro de un neumático es igual a su presión promedio en el suelo? está relacionada.

Si podemos ignorar la rigidez de los neumáticos, entonces la presión de aire en los neumáticos multiplicada por las cuatro áreas de contacto de los neumáticos debe ser igual al peso del coche, por lo que la presión estaría dada por:

$$ P = \frac{Mg}{A} $$

donde $M$ es la masa del coche y $A$ es el área total de contacto del neumático.

A primera vista, parece que $P \propto M$, y por lo tanto, aumentar el peso del coche (y su contenido) aumentará la presión del neumático en proporción. Sin embargo, el aumento de peso también aplanará la región de contacto y aumentará el área de contacto $A$, y este efecto reducirá la presión del neumático.

Supongo que podrías modelar la deformación de los neumáticos para descubrir cómo $A$ depende de $M$, pero esto me parece una tarea complicada, y no me resulta obvio qué efecto dominaría. Sin embargo, cualquier deformación del neumático reducirá su volumen y, por lo tanto, tenderá a aumentar la presión en su interior, por lo que parece probable que el aumento en el área de contacto no compense el aumento de masa. En otras palabras, la presión del neumático aumentará con la carga, pero probablemente no sería simplemente proporcional a la carga.

Answer 4

Intentaré ahondar más en la física aquí. En la práctica, el peso sin carga del automóvil no es cero, pero consideraré dos estados donde el primer estado se refiere a ningún peso en la llanta. Para hacer un cálculo práctico para el automóvil, entonces, utilizarás los números para el segundo estado, restando el peso de un vehículo del otro.

Hay dos ecuaciones principales que veo en acción, y éstas han sido presentadas en otras respuestas, aunque no en tantas variables. Otra vez, usaré "estado 1" para denotar ninguna carga y "estado 2" para el estado cargado.

$$ P_1 V_1 = P_2 V_2 $$

Una nota sobre la justificación: esto asume que la temperatura está fijada. Hay un sumidero de temperatura infinito disponible en forma del entorno ambiente. Entonces tendrás algún cambio de temperatura si cargas un vehículo rápidamente, pero con el tiempo la temperatura de la llanta está dictada completamente por las condiciones de funcionamiento. Pasando a la segunda ecuación que tengo en mente, igualamos la superficie de contacto y la presión sobre esa superficie al peso que se está sosteniendo. Estoy asumiendo que la llanta no tiene peso.

$$ A_{ft,2} P_2 = M g $$

Para el estado 1, esta es una ecuación trivial, así que no la escribo. El A, área, aquí es el área de la huella. Esto es diferente del área total geométrica de la llanta. Esto es solamente el área de contacto entre la llanta y el suelo. Tendré que ignorar cualquier contribución de la rigidez de la propia llanta.

Sería un asunto simple igualar el área de la huella de un toro al volumen restante sobre el suelo. Sin embargo, la ecuación de toro es complicada. Asumiré una llanta esférica. Esto es aún más detallado que cualquier otro intento hasta ahora, aunque la puerta está abierta si alguien quiere hacer más trabajo.

$$ A_{ft} = \frac{M g }{ P} = \pi \left( R^2 - (h-R)^2 \right) = \pi ( 2 R h - h^2 ) \\ V = \int_{h-R}^{R} \pi \left( R^2 - z^2 \right) dz = \left[ z R^2 - \frac{1}{3} z^3 \right]_{h-R}^{R} \\ = \pi \left( \frac{4}{3} R^3 - h^2 ( R - \frac{1}{3} h ) \right) $$

Para aplicar esto, para el estado sin carga, observa que h=0. Para el estado cargado, la primera ecuación arriba se puede resolver para la altura de desplazamiento. Imaginaremos que conocemos la presión de la llanta sin carga, así que todo en esa ecuación está resuelto. Ahora podemos regresar a la ecuación P1 V1 = P2 V2, y resolver para P2. El término V1 es simplemente el volumen de una esfera perfecta. Luego, tenemos V2 en términos de h, y tenemos h en términos de P2. Esto produce una ecuación que puedes resolver para P2, aunque es un polinomio de alto orden.

Aquí hay algunos números, que representan vagamente un Corolla.

• P1 = 30 psi = 206842.7 Pa
• R = 28.85/2 pulgadas = 0.3155 metros

Insertando estos números, podemos resolverlo numéricamente. Sin embargo, al hacer esto, necesitamos corregir la suposición exagerada de una llanta esférica, así como tener en cuenta las 4 ruedas. Un volumen típico de la llanta está en el orden de 10 L, y la esfera en mi caso es de 131.5 L. Entonces, por realismo, estoy corrigiendo la carga por la proporción entre estos dos, 131.5 L a 40 L.

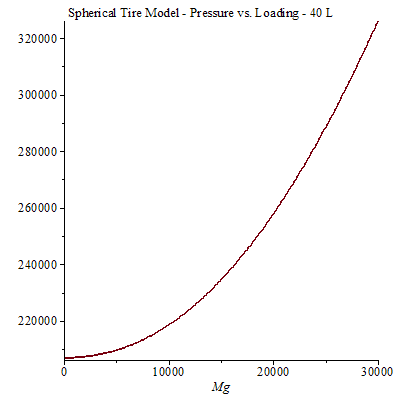
Con eso, aquí están los números que obtengo. Esta es la presión en Pa versus la carga del automóvil en Newtons.

EDICIÓN: Esta es la segunda versión corregida del gráfico. Todavía utiliza todos los parámetros anteriores, pero ten en cuenta que esto asume 40 L de volumen total de la llanta. Había olvidado un factor de pi.

Ahora esto asumió una esfera, y también ten en cuenta que el eje y no comienza en cero. La no linealidad se debe a los cambios en la huella a medida que la altura de la depresión primero supera 0. Dado que la geometría real de la llanta comienza con un área de contacto mucho más plana para empezar, se sigue que gran parte de la curva inicial aquí no se observaría en la práctica.

Sin embargo, cuando estamos aproximadamente en 1 tonelada métrica de carga, la altura de la depresión es cerca de la mitad del radio. Geométricamente, creo que este punto se asemejaría un poco a la relación de huella a volumen de las llantas normales, y la segunda derivada de la curva anterior es similar a lo que veríamos en la práctica. Además, el área de contacto ajustada en este ejemplo resulta ser aproximadamente 0.06 m^2, lo cual es muy similar a lo que esperaría calculando algunos números simples sobre el Corolla.

Esta no linealidad es mucho más de lo que esperaba, y también un efecto mucho mayor del peso del automóvil en la presión de la llanta. Ciertamente creería que podrías causar algunos problemas al no tener en cuenta el impacto de la carga en la presión de la llanta.

---

ADICIÓN:

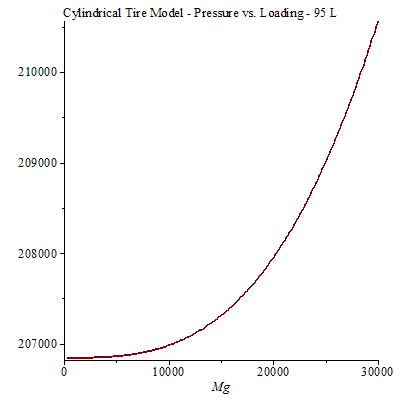
Realmente debería haber asumido un modelo de cilindro. Básicamente, imaginas que todas las llantas son cilindros orientados horizontalmente, con un agujero en el medio para el cubo. Esto es realista hasta cierto punto, y si tienes las dimensiones, entonces no se necesita ningún factor de corrección como en el ejemplo anterior.

Las medidas de la llanta que asumí fueron:

• R = 0.292 m
• Rin = 0.206 m
• L = 0.711 m

Aquí, la "L" es el ancho de las 4 llantas, si teóricamente estuvieran alineadas una al lado de la otra. Entonces solo es multiplicar el ancho de una llanta por 4. "Rin" es el radio del rin. Este volumen se resta del volumen total del cilindro.

Estas medidas, basadas en dimensiones externas, resultan en aproximadamente 95 L. Una diferencia importante entre esto y el ejemplo anterior es entonces el volumen. Sin embargo, la diferencia fundamental en la forma sigue siendo evidente.

Para poner esto en términos reales, si la carga es de 3 toneladas métricas, la presión de la llanta aumenta 0.5 psi en relación al estado sin carga. Su peso normalmente causa solo alrededor de 0.05 psi por encima de la presión normal de la llanta.

El Corolla pesa alrededor de 1.3 toneladas. La carga máxima legal es de 0.45 toneladas. Si asumimos un error de 0.5 psi en un medidor de presión, parece razonable.

Por lo tanto, mi conclusión es que no hay una manera legal de medir este efecto en tu garaje.

Answer 5

La primera explicación en la pregunta es correcta: la presión de los neumáticos aumenta con una carga creciente.

La segunda explicación tiene un problema en que la frase "la cantidad de aire dentro del neumático es constante" es demasiado vaga en cuanto a lo que significa "la cantidad de aire". El número de moléculas de aire dentro del neumático permanece constante. Pero el volumen de aire no permanece constante; el volumen disminuye con una carga creciente. Esto significa que la presión aumenta debido a la ley de Boyle, que dice que para un número constante de moléculas de gas a una temperatura constante, la presión del gas es inversamente proporcional a su volumen, $$P \propto 1/V \ \ .$$

Puede resultar poco intuitivo que la presión y el volumen estén tan estrechamente relacionados para el aire, porque la mayoría de las otras cosas que se encuentran en la vida cotidiana no se comportan de esa manera. Los objetos sólidos en general tienen muy poca compresibilidad. Y aunque los líquidos son más similares a un gas que a un sólido en que los líquidos son fluidos como los gases, los líquidos y los gases son diferentes en que los líquidos son un fluido incompresible, pero los gases son un fluido compresible.