Creando polígonos alrededor del alcance de puntos similares con ArcGIS Desktop?

Question

Tengo millones de puntos recopilados para la capa de litología.

Se ha utilizado un código para diferentes tipos de rocas.

Necesito crear un polígono alrededor de la extensión de puntos similares.

¿Cuál es la forma más fácil de obtener el polígono en lugar de digitalizar manualmente?

Estaba buscando herramientas que conviertan puntos en polígonos, pero parece que no hay ninguna.

He visto herramientas para convertir líneas en polígonos, polígonos en líneas y puntos, pero no para puntos a polígonos.

Answer 1

Es importante tener en cuenta que estos datos son muestras de dominios litológicos discretos. A menudo, el límite entre dos de estos dominios no puede ser identificado en el campo, por lo que no es válido esperar que muchas de las ubicaciones de las muestras estén precisamente a lo largo de los límites. Una solución correcta será una partición del área de estudio y cada polígono dentro de esa partición podría (y a menudo lo hará) extenderse más allá de las ubicaciones de las muestras que lo determinan. Excepto para aproximaciones burdas, esto descarta cualquier enfoque que utilice las ubicaciones de las muestras como vértices de los polígonos resultantes.

Para un trabajo de alta calidad, el mejor método es ajustar un modelo espacial lineal generalizado para un proceso multinomial. Ese es un procedimiento que requiere considerable experiencia y esfuerzo. Como alternativa, podría considerar expandir cada punto de muestra en su polígono de influencia (también conocido como polígono de Thiessen, polígono de Voronoi o celda de Dirichlet). Limitar la expansión a áreas terrestres es una buena idea; esto se puede hacer con una cuadrícula de máscara.

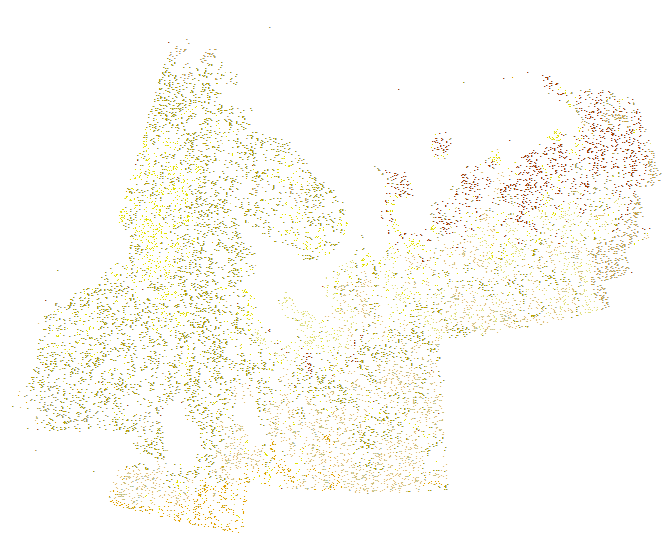
Para ilustrar, considere este conjunto de datos mucho más pequeño (de 14,136 puntos) que representa 12 clases litológicas distinguidas por color:

Aquí hay un detalle del centro del lóbulo oriental, mostrando las posiciones irregulares de los puntos y los cambios relativamente rápidos de litología allí. Seguir esto manualmente sería un procedimiento difícil y arbitrario:

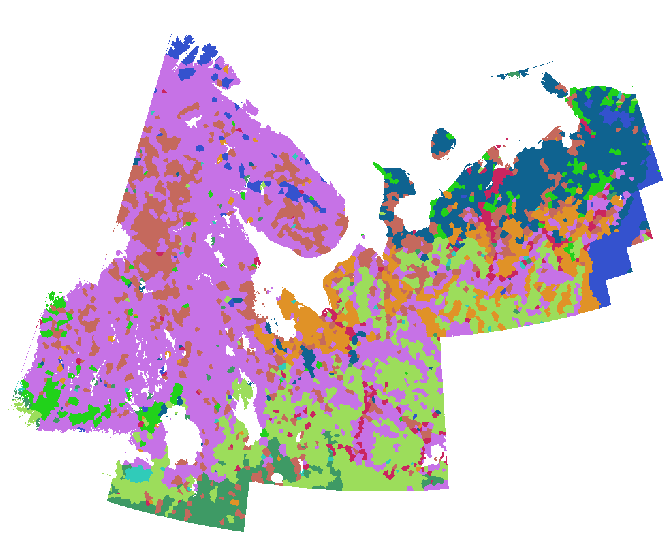
Logré la expansión convirtiendo estos puntos en una cuadrícula (alrededor de 800 filas y 1000 columnas) y calculando su asignación euclidiana, utilizando una máscara que limitaba el cálculo a tierras no glaciadas. (La paleta de colores en las próximas dos figuras difiere de la anterior.)

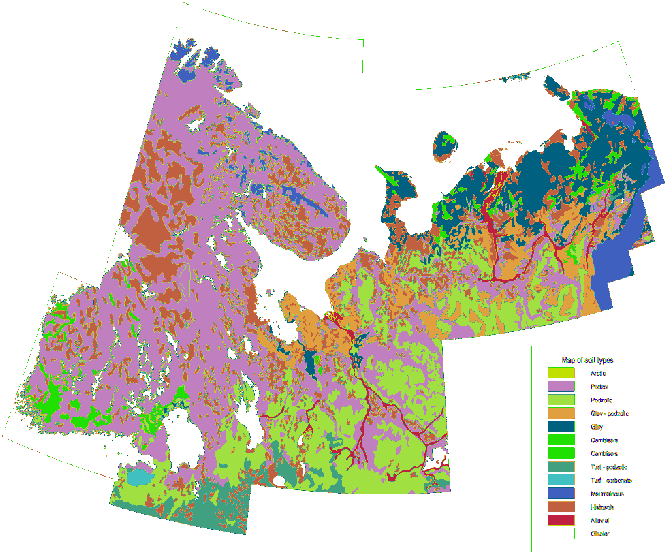
Para comparación, aquí hay un mapa litológico detallado de la misma área dibujado a la misma escala con la misma simbolización:

Con un conjunto de datos verdaderamente grande o un área de estudio complicada, puede ser conveniente dividir la región en mosaicos y realizar este procedimiento por separado en cada mosaico, fusionando los resultados en un raster de salida si se desea. Para que esto funcione, los mosaicos deben superponerse ligeramente para evitar efectos de borde (y luego se deben recortar uniformemente antes de fusionar).

Las razones principales para utilizar una representación raster son (1) es rápido y fácil de calcular y (2) las soluciones precisas basadas en vectores serán difíciles de obtener. Si intenta con búferes, envolturas convexas, envolturas cóncavas, o cualquier otra cosa, encontrará que todas ellas se intersectan mutuamente y aún dejan espacios vacíos: en otras palabras, no producirán una partición topológicamente consistente del espacio en dominios litológicos distintos.

Un método basado en vectores que funcionará es computar una teselación de Voronoi restringida de los puntos (buenos métodos llevan tiempo O(n*log(n)) para n puntos), fusionar espacialmente las celdas de Voronoi de acuerdo con los atributos litológicos de sus puntos asociados, y luego separar los multipolígonos resultantes en sus componentes conectados (si así lo desea). Sin embargo, si todo lo que necesita es salida en formato de vector, es más fácil regionar el resultado raster y convertirlo a formato vectorial.

Answer 2

Puedes intentar crear Polígonos de Thiessen a partir de los puntos y luego disolver los polígonos resultantes utilizando el atributo del tipo de roca.

Answer 3

Interpolación 3D para construir sólidos luego corte de sección horizontal a una profundidad para atravesar la litología y obtener polígonos - Según sus últimos comentarios, parece que estamos tratando con datos de perforaciones en 3D. Esto significa que primero deberá construir sólidos en 3D (mallas trianguladas) a partir de sus datos. Hay 2 formas de hacer esto: Digitalizando los contactos en 3D para crear los sólidos de litología o interpolación 3D. Para hacerlo de forma manual, necesitará software como GEOMCOM GEMS o similar y el único paquete que conozco que puede hacer esto de manera dinámica es Leapfrog Mining. (Que es lo que yo utilizo) Los modelos manuales tienden a ser más simples y permiten la interpretación humana de la geología, pero la actualización es difícil. Los modelos dinámicos pueden tardar un poco en configurarse, pero a medida que su programa avanza y se dispone de nuevos datos, simplemente puede actualizar y regenerar modelos de litología actualizados. Ambas técnicas son bastante complejas de explicar aquí. Probablemente recomendaría digitalizar manualmente para modelos más simples o donde no va a estar actualizando el modelo con nuevos datos a futuro. Leapfrog Mining es una aplicación muy pulida y tiene toda una estructura de dominio en 3D en la que se puede definir correctamente la litología de la más antigua a la más joven, por ejemplo, pero se requiere entrenamiento para entender este concepto.

Una vez que tenga creado su modelo de litología, simplemente se trata de crear una sección de corte orientada horizontalmente a una profundidad específica. Luego puede exportar los contornos de la litología a polígonos que forman la base de su mapa de litología. Puede bajar la sección varias veces a intervalos para luego comparar cómo cambia la litología a diferentes profundidades.

Esto también puede ser visualizado en Leapfrog, pero a menudo exporto los modelos 3D a DXF y uso otras aplicaciones como Geosoft Target para crear secciones más tradicionales utilizando estos sólidos.

Solo describí mi flujo de trabajo pero estoy seguro de que hay otras soluciones; es posible generar un modelo de litología en Geosoft Target, pero no lo he intentado simplemente porque no me gusta trabajar con este software. Estoy bastante seguro de que Datamine Studio también se puede utilizar o incluso puede ser superior a mis técnicas.

Answer 4

Es su problema "necesito crear un polígono alrededor de la extensión de puntos similares"? Trate de rectángulo( punto(min(x),min(y)), punto(max(x),max(y)) ) ... o ser más específico.

Answer 5

Puedes intentar usar el Asistente de Buffer en ArcMap.

Puedes intentar utilizar cualquier tipo de métrica o distancia, pero probablemente necesites averiguar cómo hacer coincidir o tal vez utilizar su plantilla de extensión si la hay.

Puede que quieras encontrarlo en ArcScripts o en el geoprocesamiento del sitio web de soporte de ESRI.