Aunque usted podría encontrar esas secuencias, que sería más probable que ellos mismos hacen uso intenso de la $\pi$. Por esta razón, lo mejor que se podía esperar alguna secuencia de lo que se podía factor $\pi$ de manera tal que el resultado se suma a $1$.
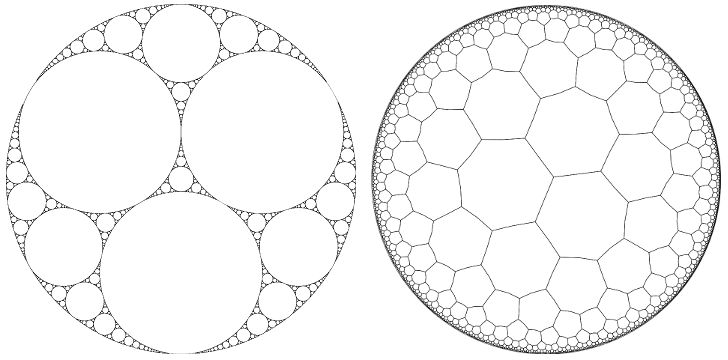
Apolíneo junta
Usted puede utilizar de Descartes teorema para calcular el (inverso) círculo de los radios, a partir de cuatro. Para la configuración simétrica de su imagen sugiere, estos no serán integral (ver Wikipedia en casi $D_3$ simetría en este contexto). Más precisamente, de acuerdo a esta sección de Erich embalaje centro de los radios de las ti más grande de los círculos se $r=\frac{3}{2\sqrt3 + 3}$. Así que usted puede calcular posterior de los radios de estos, dada la suficiente paciencia. A su vez, todos estos radios de nuevo en las áreas que le gustaría plaza de ellos y los multiplicamos por $\pi$. Así que si usted aprende que el cuadrado de la suma de los radios de seguridad de a $1$, esto no decirte un poco acerca de el valor de $\pi$.
Hiperbólico mosaico
Parece que usted está utilizando el disco de Poincaré modelo de la geometría hiperbólica. Lo que significa que su heptagon límites de la realidad no son líneas rectas, pero en lugar de arcos de círculo, lo que hace que la distancia Euclídea área de la computación, tanto terriblemente complicado para escribir y muy íntimamente relacionado con los círculos. Por lo tanto dudo que usted puede obtener el área de expresarse sin uso masivo de $\pi$. Así que todo el resultado más probable es que aparezca como un argumento circular, perdón el juego de palabras. Una alternativa podría ser el uso hiperbólico de las esquinas, pero la conexión de ellos con líneas rectas Euclidianas. Otra alternativa podría ser la Beltrami-Klein modelo. Tampoco parece especialmente adecuado para una fácil descripción de la secuencia de $\pi$, sin embargo.