En los números naturales, la función totiente de Euler $\phi(n)$ tiene la bonita propiedad de que $\phi(n^m)=n^{m-1}\phi(n)$. He encontrado que esto puede extender ingenuamente la función totiente a los números racionales a través de: $$\phi(b)=\phi\left(\left(\frac{1}{b}\right)^{-1}\right)=\left(\frac{1}{b}\right)^{-2}\phi\left(\frac{1}{b}\right)=b^2\phi\left(\frac{1}{b}\right)$$ $$\implies\phi\left(\frac{1}{b}\right)=\frac{\phi(b)}{b^2}$$
Así, con otra propiedad siendo que $\gcd(a,b)=1\implies \phi(ab)=\phi(a)\phi(b)$, entonces bajo la suposición de que $\gcd(a,b)=1\implies\gcd\left(a,\frac{1}{b}\right)=1$, podemos definir
$$\phi\left(\frac{a}{b}\right):=\frac{\phi(a)\phi(b)}{b^2}$$
Nota que esto todavía preserva la consistencia sobre los números naturales: $$\phi\left(\frac{a}{1}\right):=\frac{\phi(a)\phi(1)}{1^2}=\phi(a)$$
Con esto, de inmediato me dio curiosidad si una secuencia de números racionales $q_n$ que converge a un irracional, ¿convergería también $\phi(q_n)$, y si es así, a qué?
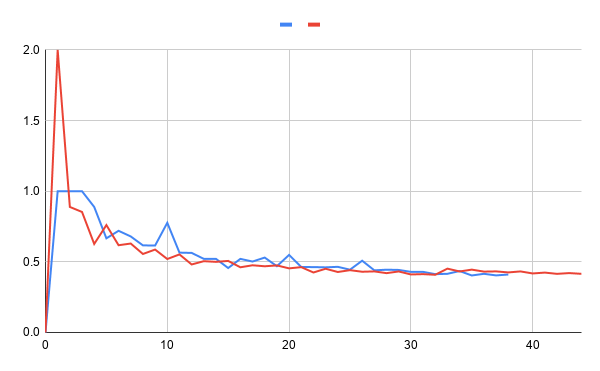
Como prueba inicial, usé la secuencia $\pi_n=\sum_{k=0}^n\frac{4(-1)^k}{2k+1}$. Que, como sabes, converge a $\pi$. Además probé la secuencia $e_n=\sum_{k=0}^n\frac{1}{k!}$ (que converge a $e$, respectivamente). Para mi sorpresa, descubrí que con esta definición de $\phi$, parecía que tanto $\pi_n$ como $e_n$ convergen.
El gráfico de $\phi(e_n)$ está en azul, y $\phi(\pi_n)$ en rojo. Curiosamente, (quizás debido a la cercanía de $\pi\approx e$), ambos parecen aproximarse a un valor de alrededor de $0.4$. Dicho esto, mi computadora y yo solo tuvimos paciencia para calcular los primeros $40$ términos, así que me gustaría mucho saber cuál es el comportamiento a largo plazo del gráfico.
Cualquier información sería muy apreciada.
Anexo: 13 de mayo
Con los comentarios que he recopilado, he realizado más análisis, que puede resultar interesante para algunos de ustedes. Específicamente, no parece que la totiente de todas las secuencias racionales convergentes converja. Por ejemplo, con sugerencias de Conifold, probé la secuencia de racionales definida por la fracción continua para el número áureo. Que se puede simplificar a $\varphi_n=\frac{F_{n+1}}{F_n}$, donde $F_n$ es el n-ésimo número de Fibonacci. Parecía evidente a partir del análisis computacional que $\phi(\varphi_n)$ no convergía, sin embargo parecía evidente que $\limsup_{n\to\infty}\phi(\varphi_n)=\varphi=\frac{1+\sqrt{5}}{2}.$. El promedio y el $\liminf$ también parecían converger, sin embargo el $\limsup$ parecía dar resultados más canónicos; en otras secuencias también.
En el caso de $\sqrt{2}$, podría ser definido por $\phi(\sqrt{2})=2^{\frac{1}{2}-1}\phi(2)=\frac{\sqrt{2}}{2}$, que parecía ser exactamente a lo que convergía el $\limsup$ al tomar la fracción continua para $\sqrt{2}$.
Por último, y quizás lo más curioso, si definimos $e_n:=\left(\frac{n+1}{n}\right)^n$ (como $\lim_{n\to\infty}e_n=e$), entonces, asumiendo que mi matemática es correcta, podemos deducir
$$L=\limsup{\phi(e_n)}=\limsup_{n\to\infty}{\phi\left(\left(\frac{n+1}{n}\right)^n\right)}=\limsup\left(\frac{n+1}{n}\right)^{n-1}\frac{\phi(n)\phi(n+1)}{n^2}$$ $$\implies \ln L = \limsup(n-1)\ln\left(\frac{n+1}{n}\right)+\ln\left(\frac{\phi(n)}{n}\right)+\ln\left(\frac{\phi(n+1)}{n}\right)$$ $$=1+\ln 1+\ln 1$$ $$\implies L=e$$
Sin embargo, en mis análisis computacionales, parecía que $\limsup \phi(e_n)\approx \frac{e}{2}$
No estoy seguro de qué se puede deducir de esto, sin embargo encuentro estos resultados interesantes, así que quizás ustedes también.