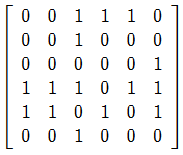Teoría de grafos: encontrar los componentes conectados del grafo dado la matriz

Question

Dibujé el grafo pero es un completo desastre, así que supongo que hay alguna fórmula para esto.

Confieso que no estoy del todo seguro de lo que se supone que debo hacer aquí. Creo que se supone que debo encontrar subconjuntos de vértices entre los cuales hay un camino hacia cada uno de ellos. ¿Así que tal vez tengo que encontrar el vértice o vértices que conectan de alguna manera los dos componentes?

Answer 1

Escribir la matriz como una lista de adyacencias \begin{array} & & & 1\to 3 & 1 \to 4 & 1 \to 5 \\ & & 2\to 3\\ & & & & & 3 \to 6\\ 4 \to 1 & 4 \to 2 & 4 \to 3 & & 4 \to 5 & 4 \to 6\\ 5\to 1 & 5 \to 2 & & 5 \to 4 & & 5 \to 6 \\ & & 6 \to 3 \end{array> Algunas de las primeras cosas que saltan a la vista son:

• $4$ y $5$ están conectados a muchas vértices y entre sí
• $3$ y $6$ están conectados entre sí y a nada más.

Entonces $\{3,6\}$ será un componente conectado, ya que cuando estás en uno de esos vértices estás atrapado y no puedes llegar a otros; $\{4,5,\dots\}$ es el comienzo de otro.

Al observar $1$, vemos que tiene conexiones con ambos componentes que hemos encontrado hasta ahora; por lo tanto, podría formar parte de uno de ellos o comenzar uno nuevo. No puede ser parte del componente $\{3,6\}$, porque esos vértices no tienen forma de llegar a $1$, pero los vértices $4$ y $5$ sí tienen conexiones de regreso a $1$ (con una de esas sería suficiente). Así que $1$ se une a $4$ y $5$ en un componente $\{1,4,5,\dots\}$.

Al observar $2$, vemos que solo tiene conexiones con $3$, por lo que es o un nuevo componente o parte del componente $\{3,6\}$. Pero no puede ser parte de ese componente, porque ni $3$ ni $6$ tienen una forma de llegar a $2$. Por lo tanto, $\{2\}$ es su propio componente.

Ahora hemos observado todos los vértices y obtenido tres componentes: $C_1 = \{1,4,5\}$, $C_2 = \{2\}$ y $C_3 = \{3,6\}$.

Answer 2

Si realmente quieres una fórmula, llamemos $A$ a tu matriz de adyacencia de tamaño $n$ (aquí, $n=6$).

$A$ representa todos los caminos de longitud 1 entre dos nodos, $A^2$ representa todos los caminos de longitud 2 entre dos nodos, etc. Cualquier camino entre dos nodos en un grafo con $n$ nodos es de tamaño como máximo $n-1$, por lo que necesitas calcular $S = \sum\limits_{i=1}^{n-1}A^{i}$. $s_{ij}$ denotará entonces el número de caminos de longitud como máximo $n-1$ entre $i$ y $j$. Existe un camino entre los nodos $i$ y $j$ si y solo si $s_{ij}$ es distinto de cero:

$$\begin{bmatrix} 1 && 1 && 1 && 1 && 1 && 1 \\ 0 && 0 && 1 && 0 && 0 && 1 \\ 0 && 0 && 1 && 0 && 0 && 1 \\ 1 && 1 && 1 && 1 && 1 && 1 \\ 1 && 1 && 1 && 1 && 1 && 1 \\ 0 && 0 && 1 && 0 && 0 && 1 \\ \end{bmatrix}$$