Encuentra el valor límite de $S=a^{\sqrt{1}}+a^{\sqrt{2}}+a^{\sqrt{3}}+a^{\sqrt{4}}+...$ para $0 \leq a < 1$

Question

Pregunta

¿Cómo puedo encontrar la suma de la serie $$S=a^{\sqrt{1}}+a^{\sqrt{2} }+a^{\sqrt{3}}+a^{\sqrt{4}}+...$$ bajo la condición $0 \leq a < 1$

Versión corta

Creo que la suma de la serie debería ser aproximadamente $$S=\frac{2} {(\ln a)^2}+c$$ donde c es un término de corrección. Entonces la pregunta es ¿cómo debo encontrar el valor de $c$?

Versión larga

Mi enfoque hasta ahora:

La suma puede reformularse en términos de $y=f(x)$ donde $$y_1=\sum_{n=1}^{\left \lfloor{x}\right \rfloor}a^{\sqrt{n}}$$ por lo que el problema ahora es encontrar el valor límite de $y_1$ a medida que $x \rightarrow \infty$. En lugar de encontrar el límite de $y_1(x)$ tal como está definido, intenté encontrar otra función con una tasa de crecimiento similar: $$\frac{\mathrm{d} y_2}{\mathrm{d} x}=a^{\sqrt{x}}$$ $${\textrm{es decir }} y_2=\int a^{\sqrt{x}}{\mathrm{d} x} $$ lo cual al resolver nos da $$y_2=\frac{2 \sqrt{x} a^{\sqrt{x}}} {\ln a} - \frac{2a^{\sqrt{x}}} {(\ln a)^2}+\frac{2} {(\ln a)^2}$$ donde la constante de integración está elegida para que la curva pase por el origen.

Al trazar ambas funciones en Desmos 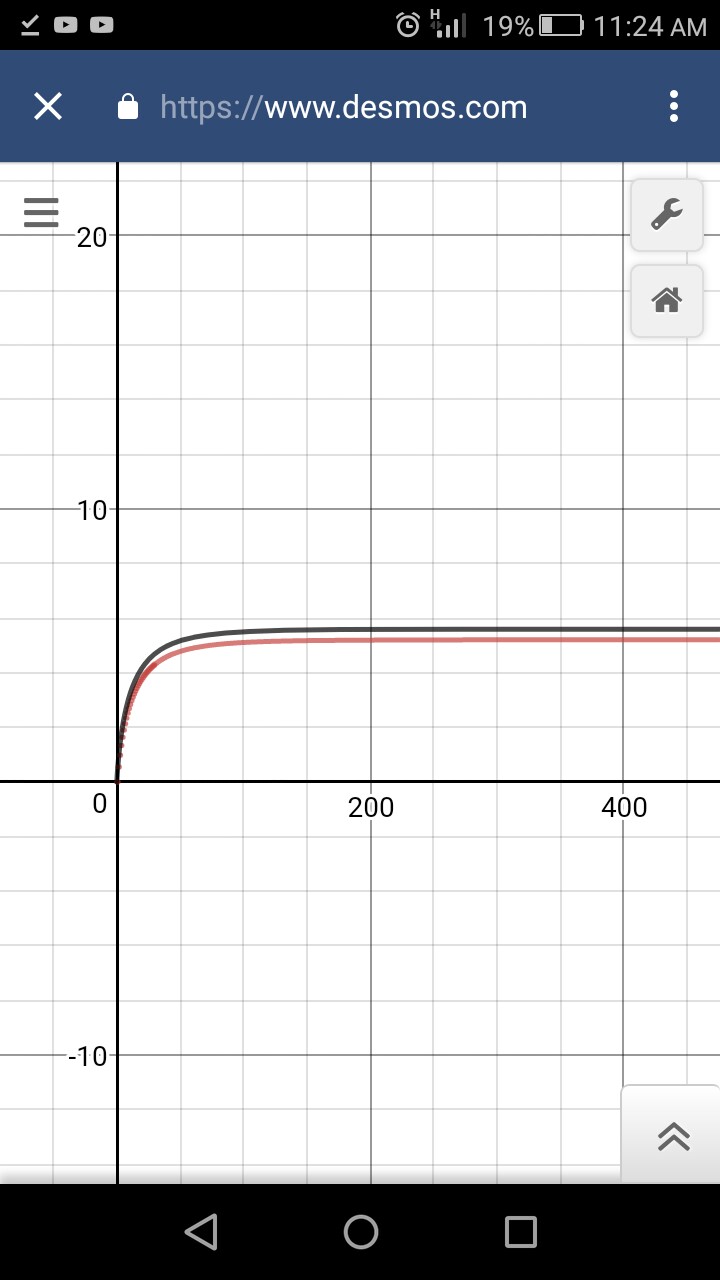se muestra que $y_1$ y $y_2$ se asemejan entre sí. Sin embargo, $y_2$ tiene un crecimiento inicial más rápido, por lo que su valor límite es ligeramente mayor que el valor límite de $y_1$ que es lo que estoy buscando. El valor límite de $y_2$ es $$S_2=\lim_{x \rightarrow \infty}{y_2(x)} =\frac{2} {(\ln a)^2}$$ Por lo tanto, creo que la suma real de la serie original debería ser: $$S=\frac{2} {(\ln a)^2}+c$$ donde $c$ es un término de corrección, posiblemente dependiendo de $a$.

Estoy atascado en cómo encontrar el término de corrección $c$ y cuál debería ser su forma. ¿Es correcto mi enfoque hasta ahora? Cualquier ayuda sería apreciada.

Answer 1

Podemos seguir en la línea de los comentarios para algo que converge tan cerca como sea necesario, comenzando desde $$ S = \frac{2}{(\log a)^2} - \frac12 + \frac1\pi \int_0^\infty \frac{e^{-\beta\sqrt{t}}\sin(\beta\sqrt{t})}{e^t-1}dt \quad\text{ donde }\quad \beta = \frac{-\log a}{2\sqrt{\pi}} $$ como lo mencionó @achille hui en los comentarios. Podemos intentar y obtener una forma para la integral, $$ I(\beta) = \int_0^\infty \frac{e^{-\beta\sqrt{t}}\sin(\beta\sqrt{t})}{e^t-1}dt $$ tomando una transformada de Mellin de la integranda con respecto a $\beta$ obtenemos $$ \int_0^\infty \beta^{s-1}I(\beta)\; d\beta = \Gamma(s)\sin\left(\frac{\pi s}{4}\right)\int_0^\infty \frac{(2t)^{-s/2}}{e^t-1} \; dt $$ esto es entonces $$ \int_0^\infty \beta^{s-1}I(\beta)\; d\beta = 2^{-s/2}\Gamma(s)\sin\left(\frac{\pi s}{4}\right)\Gamma\left(1-\frac{s}{2}\right)\text{Li}_{1-\frac{s}{2}}(1) $$ queremos tomar la transformada de Mellin inversa de ambos lados para obtener $I(\beta)$ pero no es trivial hacer esto para el lado derecho, así que invoquemos el Teorema Maestro de Ramanujan, que establece que la transformada de Mellin de $I(\beta)$ se escribe $$ \int_0^\infty \beta^{s-1}I(\beta)\; d\beta = \Gamma(s)\phi(-s) $$ tal que $$ I(\beta)=\sum_{n=0}^\infty \frac{(-1)^n}{n!}\phi(n)\beta^n $$ entonces tenemos $$ \phi(s)= \sin\left(\frac{-\pi s}{4}\right)2^{s/2}\Gamma\left(1+\frac{s}{2}\right)\text{Li}_{1+\frac{s}{2}}(1) $$ y usando $$ \text{Li}_{1+\frac{s}{2}}(1) = \zeta\left(1+\frac{s}{2}\right), \;\; s>0 $$ podemos escribir $$ I(\beta)=\sum_{n=0}^\infty \frac{2^{n/2}}{n!}\sin\left(\frac{-\pi n}{4}\right)\Gamma\left(1+\frac{n}{2}\right)\zeta\left(1+\frac{n}{2}\right)\left(\frac{\log{a}}{2\sqrt{\pi}}\right)^n $$ finalmente $$ \sum_{n=1}^\infty a^{\sqrt{n}}=\frac{2}{(\log a)^2} - \frac12 -\frac{\log(a)\zeta\left(\frac{3}{2}\right)}{4\pi} -\frac{\log(a)^2\zeta\left(2\right)}{4\pi^2}-\frac{\log(a)^3\zeta\left(\frac{5}{2}\right)}{32\pi^2}+\frac{\log(a)^5\zeta\left(\frac{7}{2}\right)}{512\pi^3}+\cdots $$