¿Dos ondas estando en fase es lo mismo que decir que las dos ondas son coherentes?

Question

Si dos ondas son coherentes, ¿es lo mismo que estar en fase? Por favor, corríjame si estoy equivocado.

Answer 1

Son dos conceptos diferentes pero estrechamente relacionados

Dadas dos ondas sinusoidales de igual frecuencia, uno puede preguntarse cuál es su fase relativa, y si están en fase o fuera de fase. Por lo tanto, $\sin(\omega t)$ y $sin(\omega t+\pi)$ tienen una fase relativa de $\pi$ o 180 grados, por lo que diríamos que están fuera de fase.

La pregunta sobre la coherencia es: ¿qué tan estable es la fase entre las dos ondas? ¿Cambia rápidamente con el tiempo? Con las dos ondas sinusoidales perfectas anteriores, la fase relativa nunca cambia. Siempre es $\pi$. Pero ninguna onda real es perfectamente sinusoidal. En su lugar, piensa en una señal que parece sinusoidal en cualquier pequeño fragmento, pero la fase está cambiando lentamente. Simbólicamente podemos escribir $f(t)\equiv sin(\omega t + \phi(t))$ donde $\phi(t)$ es una función que cambia lentamente de t. Si tenemos dos de estas señales, podemos preguntar cómo está cambiando la fase relativa. Si no cambia significativamente (como si midieramos la luz en dos partes de un haz láser), entonces diríamos que las señales son altamente coherentes. Si la fase relativa no es estable, si pasan rápidamente de estar en fase a estar fuera de fase, como la luz de una bombilla, entonces diríamos que son incoherentes. Más cuantitativamente, podemos dar un tiempo de coherencia, el tiempo que tarda en desvincularse.

Answer 2

Para que dos ondas sean 'perfectamente' coherentes (asumo ondas electromagnéticas, transversales) deben tener la misma longitud de onda, polarización y fase.

Para profundizar un poco más, la coherencia nunca puede ser perfecta.

Solo una onda infinitamente larga tiene una longitud de onda que está 'totalmente definida', es decir, no tiene incertidumbre (o ancho) asociado. Por lo tanto, se define una longitud de coherencia (o equivalente un tiempo de coherencia) sobre el cual la fase es probable que sea la misma. Entonces, si divides una onda realista (como el haz de un láser de HeNe) en dos, luego retrasas una de ellas y las vuelves a unir (por ejemplo, Interferómetro de Michelson o Mach-Zehnder), la coherencia decae en función del retraso.

Answer 3

Vamos a ubicar tu pregunta en el marco de un interferómetro Mach-Zehnder para poder definir algunas variables importantes. Aquí hay un Mach-Zehnder dibujado rápidamente en MS Paint.

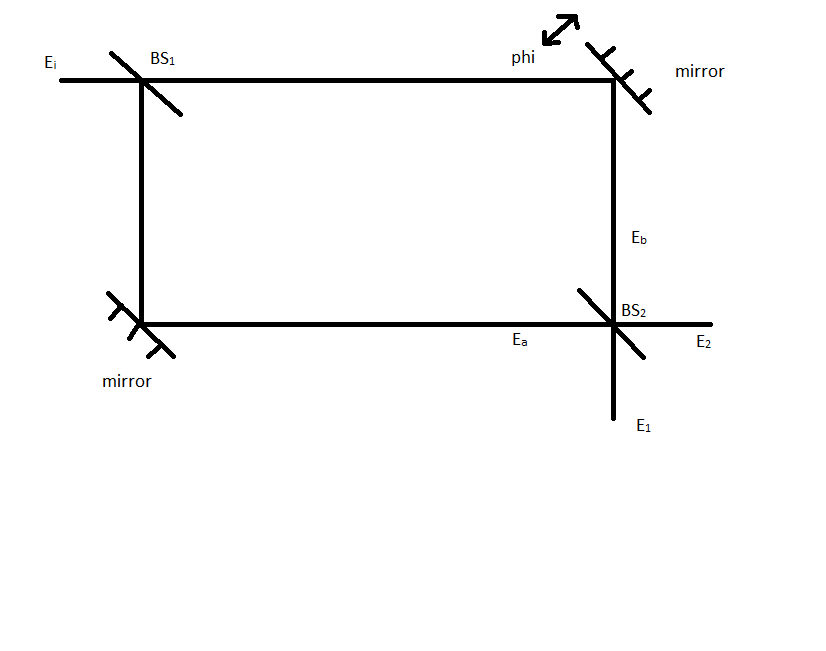
El campo eléctrico $E_{i}$ incidente en el primer divisor de haz $BS_{1}$ se divide en campos eléctricos $E_{a}$ y $E_{b}$. Si asumimos que los espejos son totalmente reflectantes, no se pierde energía y los campos se recombinan en $BS_{2}$. Al desplazar uno de los espejos, podemos ajustar la diferencia de longitud de camino y, por lo tanto, la fase relativa de las dos ondas cuando inciden en $BS_{2}$. La ecuación que rige este desplazamiento de fase es $\phi=\frac{2\pi\Delta l}{\lambda}$. Ahora, sin pérdida de generalidad, consideremos solo $E_{1}$. La ecuación para este haz es $E_{1}=r_{2}E_{a}+t_{2}E_{b}e^{i\phi}$ donde $r_{2}$ y $t_{2}$ son los coeficientes de reflexión y transmisión de $BS_{2}$ respectivamente y el factor de $e^{i\phi}$ tiene en cuenta el desplazamiento de fase relativa. Por simplicidad, asumamos que los coeficientes de transmisión y reflexión para ambos divisores de haz son iguales a $\frac{1}{\sqrt{2}}$. Entonces $E_{a}=\frac{1}{\sqrt{2}}E_{i}=E_{b}$. Aunque el campo eléctrico no se conserva, la energía sí, y podemos representar la energía mediante la intensidad (o potencia) del haz. La intensidad de $E_{1}$ se da como $I_{1}=|E_{1}|^{2}=\frac{|E_{a}|^{2}}{4}(1+e^{i\phi})(1+e^{-i\phi})=\frac{I_{i}}{2}(1+\cos\phi)$, donde $I_{i}$ es la intensidad de entrada correspondiente a $E_{i}$. Nótese que si $\phi$ es un múltiplo de $2\pi$, las ondas interfieren de manera constructiva y toda la intensidad de entrada se refleja a través de $E_{1}$.

Ahora hablemos de coherencia. Si la diferencia de longitud de camino entre los dos brazos de nuestro interferómetro es casi cero, y asumimos que los espejos están construidos de manera estable y no propensos a vibraciones. La diferencia de fase entre los haces es entonces constante y decimos que los haces son coherentes. Sin embargo, digamos que vibramos rápidamente uno de los espejos, con una amplitud de vibración mayor que la longitud de onda de la onda. Si las vibraciones son extremadamente rápidas, es decir, más rápidas de lo que nuestro detector puede registrar, el detector promediará la vibración. La intensidad promedio $I_{1}$ es entonces igual a $\frac{I_{i}}{2}\langle(1+\cos\phi)\rangle=\frac{I_{i}}{2}(1+\langle\cos\phi\rangle)$. Dado que la amplitud de las fluctuaciones es mayor que una longitud de onda, el término coseno se promediará a cero y la intensidad promedio que emerge de $E_{1}$ es $\frac{I_{i}}{2}$. El mismo proceso se puede hacer para $E_{2}$ con el mismo resultado. No observamos interferencia y los haces se llaman incoherentes. La última posibilidad es que las fluctuaciones sean igual de rápidas, pero la amplitud de las fluctuaciones es menor que una longitud de onda. Esto hace que el término $\cos\phi$ no se promedie a cero, pero la interferencia se conserva, aunque su visibilidad se reduce. Estos haces se dice que son parcialmente coherentes.

Espero que al definir cada término específicamente haya respondido a tu pregunta.

Fuente: "Quantum Mechanics: Theory and Experiment" de Mark Beck

Answer 4

Mientras que estoy de acuerdo con BebopButUnsteady, hay una manera más simple de resumir lo que dijo. La coherencia y la diferencia de fase relativa no son lo mismo. Tomemos dos señales,

$$s_1 = \sin(\omega_1t + \theta_1)\\ s_2 = \sin(\omega_2t + \theta_2)$$

Dos ondas pueden ser coherentes y estar fuera de fase. Pero no pueden tener una diferencia de fase relativa constante y ser incoherentes. El meollo del asunto es la demora de fase, theta, y las frecuencias, omega, de las dos ondas. Si las dos ondas tienen la misma frecuencia $\omega_1 = \omega_2$ y están alineadas en fase, $\theta_1 = \theta_2$, entonces son coherentes y en fase. Si las dos tienen desplazamientos de fase diferentes $\theta_1 \neq \theta_2$, pero son de la misma frecuencia, $\omega_1 = \omega_2$, entonces son coherentes y fuera de fase. Si tienen diferentes frecuencias, $\omega_1 \neq \omega_2$, son incoherentes independientemente del desplazamiento de fase.

Answer 5

Creo que "en fase" significa que la diferencia de fase de las dos ondas es cero (y fuera de fase significa que esta diferencia es igual a pi). Pero más en general, si la diferencia de fase de dos ondas permanece la misma durante un tiempo eso se llama "Tiempo de Coherencia", los campos son coherentes durante ese tiempo. En realidad, los campos no permanecen coherentes por un intervalo infinito y después del tiempo de coherencia, la diferencia de fase se desvía.