(En esta respuesta estoy usando el símbolo \require{begingroup} \begingroup \newcommand{\tb}[0]{\tilde{B}} \tb para representar un número de onda en lugar de B, que elijo definir como una energía - no será lo que utilizaremos.)
¿Por qué la separación máxima es 4\tb en lugar de 2\tb?
Esto tiene que ver con la estadística del espín nuclear. Debido a que el oxígeno-16 es un bosón (espín 0), la función de onda de toda la molécula (que comprende componentes de translación, rotación, vibración, electrónica y de espín nuclear) debe ser simétrica al intercambiar los dos átomos de oxígeno-16.
El componente de translación es simétrico, como de costumbre. El estado electrónico fundamental es {}^1\Sigma_\mathrm{g}, que es totalmente simétrico. El componente de espín nuclear debe ser simétrico en virtud del hecho de que ambos átomos de oxígeno tienen un espín 0; esto significa que solo hay un posible estado de espín en el que pueden estar (cf. el hidrógeno-1 tiene un espín de 1/2 y dos posibles estados de espín). En consecuencia, el intercambio de los átomos de oxígeno no produce cambios en la función de onda de espín nuclear.
Como resultado, esto significa que el componente vibracional multiplicado por el componente rotacional debe ser simétrico; o en otras palabras, los componentes vibracional y rotacional deben tener la misma paridad.
Dado que la estructura máxima en \pu{2349 cm-1} surge debido al estiramiento antisimétrico, el estado vibracional fundamental v = 0 es simétrico con respecto al intercambio de oxígeno, y por lo tanto debe estar asociado con niveles rotacionales con J par, que también son simétricos. De manera similar, el estado vibracional excitado v = 1 es antisimétrico y debe estar asociado con niveles rotacionales con J impar.
En \ce{CO} donde no hay estadísticas de espín nuclear en juego, las siguientes transiciones son todas permitidas en la rama R (\Delta J = +1): \begin{align} (v,J) = (0,0) &\to (1,1) & \text{línea 1}\\ (0,1) &\to (1,2) & \text{línea 2}\\ (0,2) &\to (1,3) & \text{línea 3}\\ (0,3) &\to (1,4) & \text{línea 4}\\ \end{align}
y así sucesivamente. Sin embargo, en \ce{CO2} el estado (v,J) = (0,1) no es permisible, por lo tanto, la línea 2 no aparece en el espectro. De manera similar, tampoco lo hacen la línea 4 ni la línea 6, y así sucesivamente; por lo tanto, la separación entre líneas adyacentes se duplica.
¿Por qué las separaciones máximas en la rama P son mayores que en la rama R?
Esto se debe a que la constante rotacional \tb_0 en el estado vibracional fundamental es diferente de la constante rotacional \tb_1 en el primer estado vibracional excitado. Los niveles de energía rotacional (en unidades de número de onda) son por lo tanto:
\tilde{G}(v,J) = v\omega_0 + \tb_vJ(J+1)
donde \omega_0 es el número de onda de la transición vibracional pura (es decir, el origen de la banda). Para la transición (v,J) = (0,J) \to (1,J-1) en la rama P, la energía asociada es por lo tanto
\tilde{P}(J) = \omega_0 + \tb_1J(J-1) - \tb_0J(J+1)
La separación entre líneas adyacentes en el espectro de \ce{CO2} es entonces
\begin{align} \tilde{P}(J) - \tilde{P}(J+2) &= \tb_1J(J-1) - \tb_0J(J+1) - \tb_1(J+1)(J+2) + \tb_0(J+2)(J+3) \\ &= 4J(\tb_0 - \tb_1) + 6\tb_0 - 2\tb_1 \end{align}
Puedes verificar fácilmente que si \tb_0 = \tb_1 = \tb, entonces esto se simplifica directamente a 4\tb, como se esperaba.
Sin embargo, como \tb_0 \neq \tb_1, la brecha entre líneas adyacentes adquiere una dependencia de J, ya que el término (\tb_0 - \tb_1) no es cero. En el caso del estiramiento asimétrico, resulta que \tb_0 > \tb_1 (¿puedes descifrar por qué? Se explica mejor utilizando el momento de inercia I, ya que \tb = \hbar/8\pi cI). Por lo tanto, a medida que J aumenta (es decir, a medida que nos movemos más a la izquierda a lo largo del espectro), la separación entre líneas aumenta.
Un cálculo exactamente análogo explicará por qué las líneas en la rama R tienden a "agruparse":
\tilde{R}(J+2) - \tilde{R}(J) = 4J(\tb_1 - \tb_0) + 6\tb_1 - 2\tb_0
\endgroup
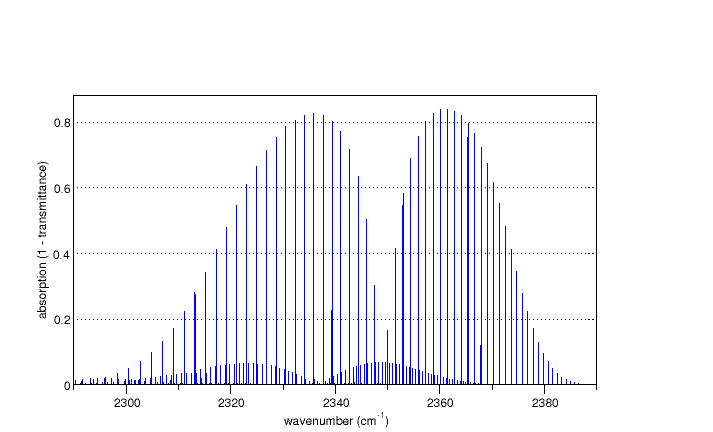 Espectro de COX2 en la región de 2349 cm−1
Espectro de COX2 en la región de 2349 cm−1

