¿Cuál es el espacio muestral en un modelo estadístico?

Question

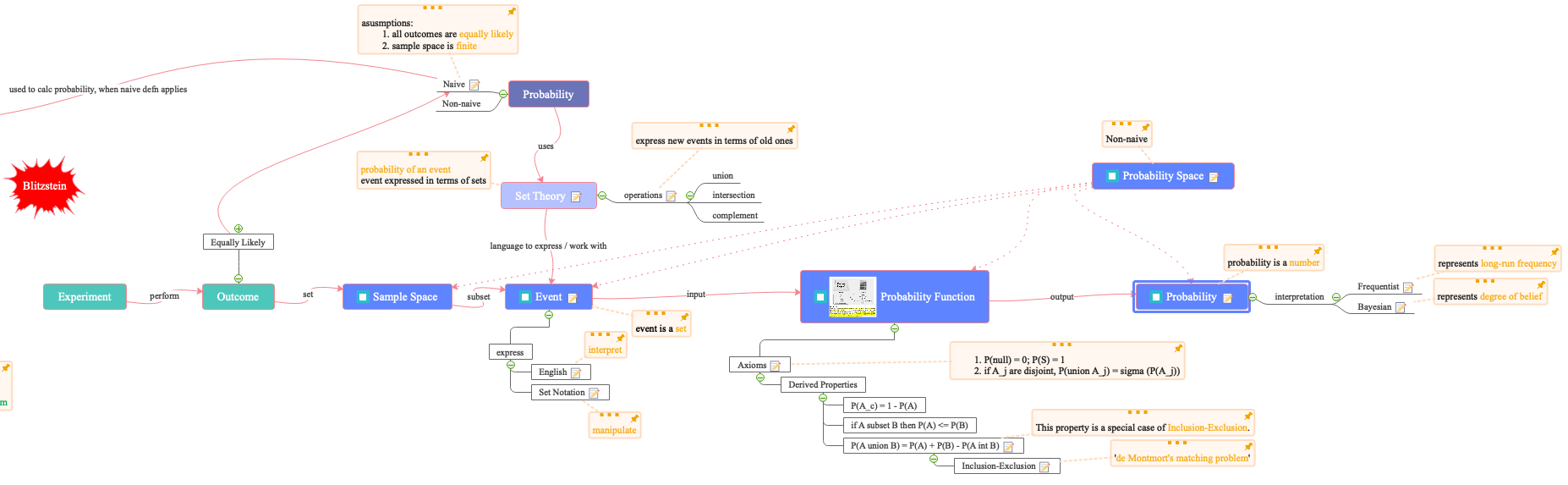
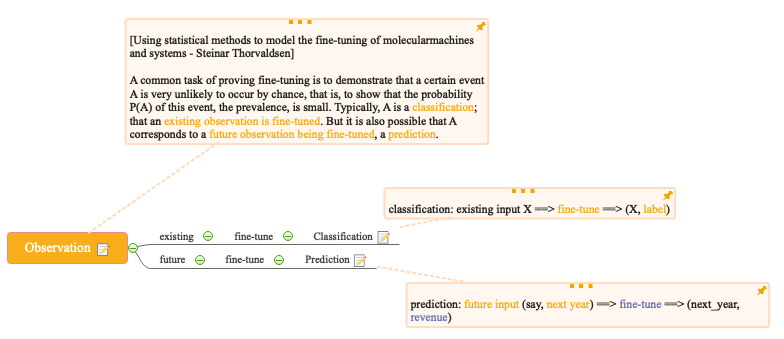
Un modelo estadístico es una tupla que contiene un espacio muestral $S$ y un conjunto de distribuciones $P$ en ese espacio muestral. Estoy obteniendo esta definición de wikipedia, "What is a Statistical Model" de McCullagh, y "All of Statistics" de Wasserman.

Supongamos que tenemos un conjunto de datos de altura y edad para un grupo de árboles, y queremos crear un modelo estadístico para predecir la altura a partir de la edad.

¿Es el espacio muestral:

1. $\mathbb{R}$ (el conjunto de posibles alturas de un árbol)
2. $\mathbb{R}^n$ (el producto de los conjuntos de alturas posibles para cada uno de los $n$ árboles en nuestros datos)
3. $\mathbb{R^2}$ (el conjunto de alturas y edades posibles de un árbol)

Después de pensarlo por un tiempo, ninguna de estas opciones parece funcionar completamente.

(1) parece razonable al principio, pero no puede ser correcto, porque no hay ningún mecanismo para condicionar la distribución a la edad, por lo que básicamente lo mejor que podríamos hacer es ajustar una única distribución a todas las alturas. Además, esto parece evitar que se pueda definir cualquier modelo que no asuma datos i.i.d.

(2) resuelve estos problemas, ya que podrías definir una distribución conjunta completa sobre todas las alturas. Sin embargo, suena extremadamente extraño porque tu modelo está básicamente "fijado" por el tamaño de los datos. Si quisieras agregar un nuevo punto de datos, o predecir la altura a partir de la edad de un nuevo árbol, necesitarías crear un modelo completamente nuevo con un espacio muestral $\mathbb{R}^{n+1}$ y luego "copiar" los parámetros, lo cual me parece bastante extraño.

Otra razón por la que esto no parece correcto es que en las notas de Larry Wasserman sobre modelos estadísticos y estadísticas suficientes, él menciona que cualquier función de $x_1, ..., x_m p(x; )$ (donde $p$ es un elemento de $P$) es una estadística, como por ejemplo la mediana. Esto sugiere fuertemente (1) sobre (2), porque no tendría mucho sentido muestrear alturas para cada uno de los $n$ árboles, $m$ veces diferentes, y luego tomar la mediana (¿qué significa eso realmente?).

(3) esto nos permite modelar la distribución conjunta de edad y altura, y luego condicionar en la edad posteriormente, por lo que parece resolver el problema sin caer en las rarezas de (2). Sin embargo, sigue siendo muy extraño que estemos obligados a modelar una distribución conjunta, incluso si queremos un modelo puramente discriminativo. Supongo que uno podría simplemente especificar p(altura, edad) = p(altura|edad)p(edad), y luego elegir literalmente cualquier distribución para la edad y ignorarla, pero esto apenas sería sensato.

Esta es una pregunta muy básica, pero he estado atascado por un tiempo, así que siento que debo haber entendido mal algo en algún lugar...

Answer 1

Para empezar, el modelo estadístico es un triple $(\Omega,\mathcal{F},P)$, donde $\Omega$ es el espacio muestral, $\mathcal{F}$ es una sigma-álgebra de subconjuntos de $\Omega$ y $P$ es una familia de distribuciones de probabilidad que pueden ser indexadas por un parámetro $\theta$.

Para aclarar las cosas, vamos a entender por qué necesitamos todas estas cosas. $\Omega$ nos dice todas las posibilidades que cada realización de un experimento aleatorio puede tomar. En su caso, cada unidad individual (un árbol) toma un par de valores $(age,height)$. Y el espacio donde este par tiene valores posibles es $\mathbb{R}^2$. Entonces supongamos que tiene datos sobre un conjunto de $n$ árboles, $X_1,...,X_n$. Cada individuo $X_i=(age_i,height_i)\in\mathbb{R}^2 \implies (X_1,...,X_n)\in\mathbb{R}^{2n}$.

El segundo elemento del modelo estadístico es una sigma-álgebra de subconjuntos de $\Omega$, que lista todos los subconjuntos de nuestro espacio muestral en los que estamos interesados en medir la probabilidad. Por ejemplo, podríamos estar interesados en medir la probabilidad de que $X_i=(age_i,height_i)\in[10,20]\times[5,10]$, es decir, la probabilidad de que un árbol individual tenga una edad entre 10 y 20 y una altura entre 5 y 10m. Para valores continuos, la sigma-álgebra común que estamos acostumbrados a tomar es la sigma-álgebra de Borel de $\mathbb{R}^n$.

Para datos discretos es más fácil entender la idea de lo que contiene la sigma-álgebra. Tomemos como ejemplo un experimento de lanzar un dado de 6 caras. En este caso $\Omega=\{1,2,3,4,5,6\}$, porque cada realización del experimento solo puede asumir uno de estos valores. Pero estamos interesados en medir la probabilidad en subconjuntos de $\Omega$. Por ejemplo, tomemos $A=\{1,2,3\}\subseteq\Omega$. Podríamos estar interesados en saber $P(A)$, la probabilidad de que una realización particular del experimento tome un valor en $A$. En otras palabras, la probabilidad de que el dado devuelva 1, 2 o 3. Además, observe que también podemos estar interesados en la probabilidad del complemento de $A, A^C=\{4,5,6\}$, o en una unión o intersección de conjuntos contenidos en $\Omega$.

Finalmente, $P$, la familia de distribuciones de probabilidad es un conjunto del cual podríamos elegir una distribución particular indexada por un parámetro, y esta distribución particular se ajusta mejor a los datos observados del experimento según algún criterio, por ejemplo, una estimación de Máxima Verosimilitud o una regresión.

En su problema, está tratando de explicar la altura basada en la edad. Eso significa que está tratando de encontrar la función de densidad que mejor describe la altura, en términos prácticos tiene una familia de distribuciones $\{f_{\theta}(height),\theta\in\Theta\}$ y está tratando de encontrar qué $\theta$ le da el mejor ajuste para la altura, y el criterio para elegir este $\theta$ es la regresión que está tratando de realizar. La edad se está utilizando como un medio para encontrar la mejor distribución para la altura. En este caso, tomamos la edad como algo dado, no como una variable aleatoria.

Creo que la respuesta sería algo así: $\Omega=\mathbb{R}^n,\mathcal{F}=\mathbb{B}(\mathbb{R}^n),P=\{f_{\theta,age}(height),\theta\in\Theta\}$

Si estuviera tratando de encontrar una densidad conjunta para la altura y la edad o algo similar, entonces estaría tratando con un modelo estadístico cuyo espacio muestral es $\mathbb{R}^{2n}$ porque estaría tratando ambas variables como random. Eso significa que podría tener los mismos datos, pero dependiendo de lo que esté haciendo, el modelo estadístico de interés puede cambiar.

Si algo está mal, se aceptan comentarios constructivos

Answer 2

Voy a mantenerlo tan simple como pueda. El espacio muestral depende de tu método de muestreo, pero en tu caso, probablemente sea $\mathbb R^n$. Veamos cómo más podría ser:

• Supongamos que decides muestrear $n$ árboles (no es realmente relevante dónde y cómo) y medir su edad y altura. En ese caso, la muestra que recopilas abarca el espacio $\mathbb R^{2n}$. Dado que decidiste el tamaño de la muestra de antemano, esa es efectivamente la dimensionalidad del espacio muestral.
• Supongamos que optas por un método de muestreo más sofisticado: sigues recopilando datos hasta que encuentres un árbol más alto que 10 metros. Puedes hacerlo absolutamente. Por supuesto, el espacio muestral ya no tiene dimensionalidad fija, simplemente no puedes expresarlo a menos que recurras a construcciones matemáticas más complejas. Puedes decir que es $\mathbb R^\infty$, pero eso no es muy preciso en realidad.
• Ahora dejemos de lado este caso excesivamente complicado, y pensemos en un ejemplo más útil: muestreas un número fijo $n$ de árboles de algunas edades específicas que te interesan (o puedes cultivarlos durante un período de tiempo fijo) y luego mides la altura. La edad no es aleatoria, depende de tu diseño experimental, por lo que la edad no se muestrea realmente. El espacio muestral es $\mathbb R^n$.
• De todos modos, en estudios observacionales donde no decides las covariables con anticipación, sino que pretendes construir un modelo de regresión, los estadísticos condicionan la muestra y el modelo en los valores de las covariables. Creo que entiendo que tienes un modelo donde la altura es la variable objetivo y la edad es la covariable, en ese caso condicionas todo en las edades observadas y cuando condicionas algo en algo más, la segunda cosa ya no es aleatoria, incluso si ha sido muestreada como en el primer caso mencionado. Es por eso que tu espacio muestral de $\mathbb R^{2n}$ se convierte en $\mathbb R^n$. Esto tiene algunas consecuencias teóricas útiles (y algunas malas también, para ser justos), y esta es la razón por la que los libros tienden a representar de esta manera los espacios muestrales en caso de modelos de regresión, pero depende del libro.

Los demás que comentaron expresaron la preocupación de que puedas decidir utilizar $\mathbb R^+$ en lugar de $\mathbb R$, y más importante aún, que tu definición de un modelo estadístico es un poco reduccionista y no muy útil. En cualquier caso, espero haberte ayudado a entender qué es el espacio muestral.

Answer 3

Un espacio muestral es un conjunto de todos los posibles resultados de un experimento aleatorio. Un evento es un subconjunto del espacio muestral. Una función de probabilidad toma un evento como entrada y produce un número real entre 0 y 1 (probabilidad).

Un modelo estocástico captura nuestra comprensión del experimento aleatorio. Para resumir todas las posibles maneras de elegir el resultado (edad, altura) de un modelo estocástico, con diferentes probabilidades, se utiliza una distribución. Esta distribución (o verosimilitud) normalmente implica algunos parámetros desconocidos (como la pendiente de edad vs altura, y el sesgo de intercepción de altura) que se infieren usando inferencia estadística. Cada configuración de parámetros posibles da lugar a un modelo estocástico diferente. La colección de todos estos modelos estocásticos se suele llamar un modelo estadístico. Por lo tanto, un modelo estadístico con parámetros desconocidos se convierte en un modelo estocástico con parámetros inferidos.

El modelo estocástico en el conjunto de datos del árbol será la edad en el eje x, la altura en el eje y y la probabilidad en el eje z. Eso convierte al espacio muestral en R^2, siendo el eje z la distribución de probabilidad (topología) en ese espacio muestral. La tarea de inferir/aprender el parámetro desconocido (por ejemplo, usando descenso de gradiente) se llama Inferencia.

Adivinar la altura dado la edad se llama predicción. Es una especie de ajuste fino donde conocemos la edad y la ajustamos finamente para incluir la altura. Esto se hace pasando la edad al modelo estocástico que produce la altura. Esto cae dentro del ámbito de la Decisión.

Referencias:

1 Blitzstein J.K., Hwang J. - Introducción a la Probabilidad-CRC (2015)

2 Utilizando métodos estadísticos para modelar el ajuste fino de máquinas moleculares y sistemas - Steinar Thorvaldsen