¿Es la función de distribución acumulada de una variable aleatoria X estrictamente creciente (X) casi en todas partes?

Question

Sea $X$ una variable aleatoria y $F_X(x) = P(X \le x)$ su función de distribución acumulativa (cdf). $P_X$ es la medida de probabilidad inducida por $X$, la cual se define como $P_X((a,b)) = P(X^{-1}((a,b))$ para $a,b \in \mathbb{R}$.

1. ¿Es correcto decir que $F_X$ es estrictamente creciente $P_X$ casi en todas partes?
2. De ser así, ¿cuál sería la manera correcta de expresarlo formalmente?
3. ¿Implica esto que $ F(x) = P(X \le x) = P(F(X) \le F(x))$ ?

He visto que la igualdad en la pregunta 3 se utiliza para demostrar la transformada del integral de probabilidad. Creo que no es tan directo demostrar 3. si $F_X$ no es estrictamente creciente.

Intenté responder a estas preguntas, considerando algunos comentarios muy útiles de whuber y Zhanxiong (quienes proporcionaron explicaciones detalladas de la transformación de probabilidad aquí y aquí).

Mi intento va hasta ahora:

¿Es correcto decir que $F_X$ es estrictamente creciente $P_X$ casi en todas partes?

En realidad no, ya que las afirmaciones casi en todas partes se refieren a propiedades de puntos individuales. La monotonía estricta no es una propiedad de un solo punto.

¿Cuál sería la manera correcta de expresarlo formalmente?

Se cumple que para cualquier $a \le b$ con $F_X(a) = F_X(b)$ que $$P_X((a,b)) \le P_X((a,b])) = F_X(b) - F_X(a) = 0$$ Así que es mejor decir que "La monotonía estricta no se cumple solo en conjuntos de medida 0" (por whuber)

¿Esto implica que $F_X(x) = P(X\le x) = P(F(X) \le F(x))$ ?

Sí. Ver: la respuesta de Zhanxiong para una versión más corta. Editar: He adaptado este intento de demostración un par de veces siguiendo recomendaciones de los comentarios.

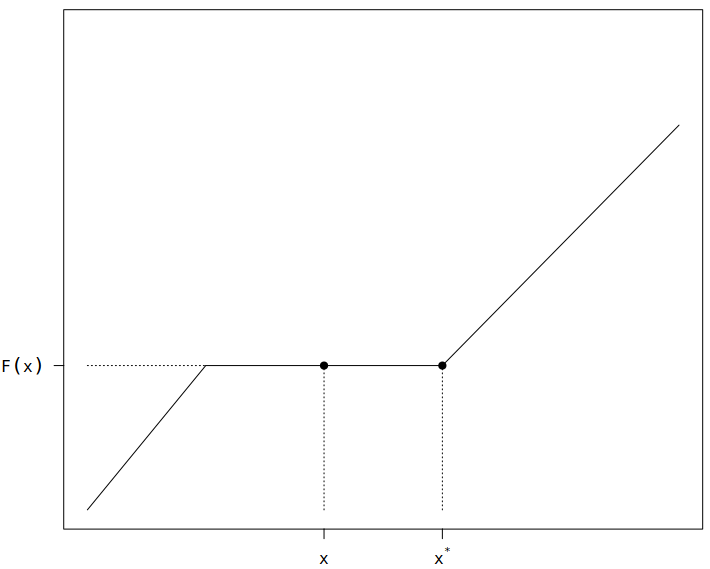
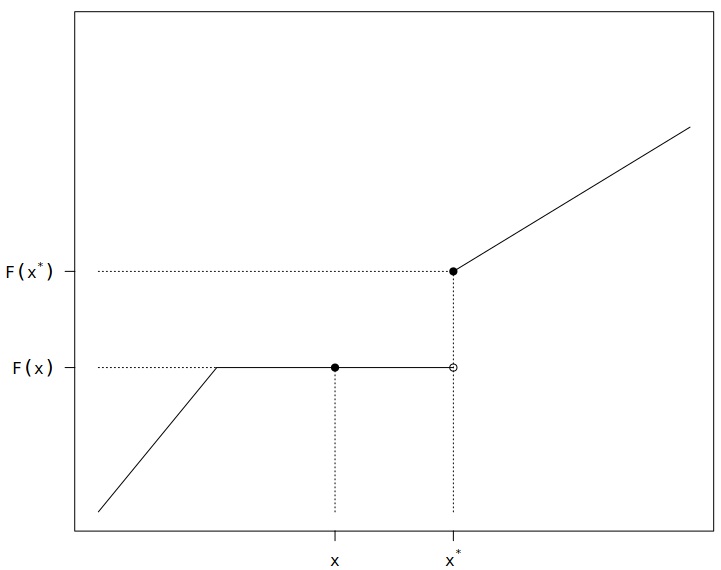
Considera un $x$ fijo en $\mathbb{R}$. Dado que $F_X$ es monótonamente creciente, $$ \{ X > x, F_X(X) \le F_X(x) \} = \{ X > x, F_X(X) = F_X(x) \}$$ Se cumple que $$P(\{ X> x, F_X(X) = F_X(x) \}) = 0 $$ Para ver esto considera $x_0 $ tal que $$x_0 = \text{sup}\{y\mid y> x, F_X(y) = F_X(x) \}$$ Entonces $F_X(y) = F_X(x)$ para todo $x_0> y > x$ y por lo tanto $$P(\{X> x, F_X(X) = F_X(x) \}) = P_X((x, x_0)) =0$$

Por la monotonicidad tenemos $$\{X \le x \} \subseteq \{F_X(X) \le F_X(x) \} $$ De ello se sigue que $$P(\{ F_X(X) \le F_X(x) \})= P(\{X\le x \})$$

¿Hay una manera más fácil de demostrar 3.? Esperé que fuera directo.

Otra pregunta que tengo es,

4. ¿Podemos decir que $F_X$ es estrictamente creciente en la imagen de $X$ ?

No estoy seguro de esto, pero supongo que podemos eliminar todos los valores de la imagen de $X$ que ocurren con probabilidad 0 y entonces sería cierto.

Answer 1

Para tu pregunta específica "¿Hay una manera más fácil de mostrar 3.?", la respuesta es "Sí". El problema de tu "demostración" no es solo su verbosidad (por ejemplo, no creo que sea necesario introducir "$\omega$" en la prueba), sino más importante aún, probablemente sea incorrecta (en mi opinión, muchos pasos son difíciles de justificar).

Aquí está mi demostración discutiendo el rango de $F(x)$.

Caso 1: $F(x) = 1$. En este caso $P[X \leq x] = F(x) = 1$. Por otro lado, claramente tenemos $P[F(X) \leq 1] = 1$. Así que $P[X \leq x] = P[F(X) \leq F(x)].

Caso 2: $0 \leq F(x) < 1$. Para simplificar, denotemos por $C$ el conjunto de todos los puntos continuos de $F$ y definamos $x^* := \sup\{y \geq x: F(y) = F(x)\}$. Debido a que $F(x) < 1$, tenemos que $x^* < \infty$. Hay los siguientes dos subcasos:

• $x^* \in C$. En este caso \begin{align*} P[F(X) \leq F(x)] = P[X \leq x^*] = F(x^*) = F(x). \end{align*} Para ayudarte a entender la geometría de este caso, mira el gráfico de $F(\cdot)$ a continuación:

• $x^* \in C^c$. En este caso \begin{align*} P[F(X) \leq F(x)] = P[X < x^*] = F(x^*-) = F(x). \end{align*} Como en el subcaso 1, a continuación se muestra el gráfico ilustrando la identidad anterior.

Esto completa la demostración.