La mayoría de los ejemplos que encontré en Internet explican bien la retropropagación en la capa de convolución, pero solo con un único kernel y un único canal de entrada.
No entiendo cómo hacer la retropropagación para más de un kernel y más de un canal de entrada.
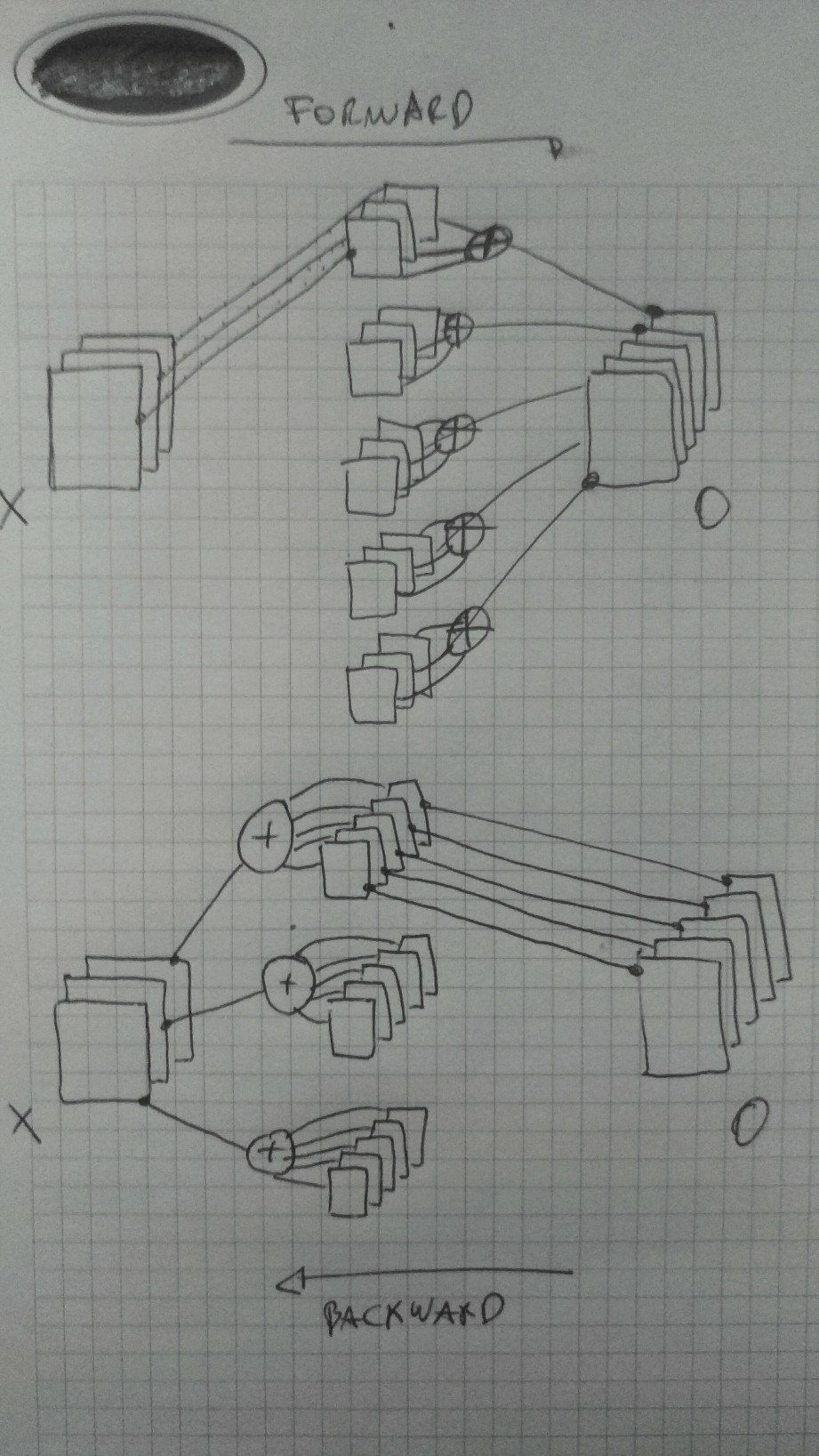
Supongamos que tengo una capa de convolución que acepta una entrada $X$ de tamaño 3x20x20, aplica 5 filtros de kernel 3x3x3 $K$ y produce una salida $O$ de tamaño 5x18x18
En un diagrama se ve así (pido disculpas por mi horrible dibujo a mano): 
Durante la pasada hacia atrás, la capa recibe un error $\frac{\partial E}{\partial O}$ y lo propaga de vuelta a la capa anterior.
Según entiendo, para calcular $\frac{\partial O}{\partial X}$ necesito aplicar una convolución 'completa' a $\frac{\partial E}{\partial O}$ con kernels rotados 180°. Entonces, se ve así:
Las dimensiones de $\frac{\partial O}{\partial X}$ deberían coincidir con las dimensiones de $X$ (3x20x20), pero la operación de convolución produce una salida con una profundidad igual al número de kernels (en mi caso 5).
Mi pregunta es ¿cómo una convolución 'completa' entre $\frac{\partial E}{\partial O}$ 5x18x18 sobre 5 filtros rotados 3x3x3 puede producir una salida $\frac{\partial O}{\partial X}$ con dimensiones 3x20x20? ¿No es cierto que la profundidad de la salida de la operación de convolución es igual al número de filtros?
