¿Funciona la mecánica newtoniana en coordenadas polares?

Question

Nuestro profesor sugirió que la Mecánica Newtoniana sólo se aplica en coordenadas cartesianas. ¿Es esto cierto?

Él dio este ejemplo.

Supongamos que hay un tren moviéndose con velocidad constante $\vec{v}=v_0\hat{x}$, con vector de posición inicial $\vec{r}=(0, y_0)$, donde $v_0,y_0$ son constantes. Él argumentó que la segunda ley de Newton no se cumpliría en coordenadas polares. ¿Alguna idea?

(Podemos suponer casos en 2D o 3D también, por lo que esféricas o polares, en realidad no importa)

Answer 1

Tu profesor está equivocado. $\vec F = m \vec a$ es válido en cualquier sistema de coordenadas inercial (no acelerado). Debes tener en cuenta que los vectores unitarios de posición en algunos sistemas de coordenadas (como el polar) no tienen una dirección constante y cambian con el tiempo. Consulta un buen texto de mecánica física, como Mecánica de Symom, para obtener la aceleración correcta $\vec a$ en esos sistemas de coordenadas, donde se tiene en cuenta correctamente las derivadas temporales de los vectores unitarios de posición.

Answer 2

De hecho, la mecánica newtoniana puede hacer que funcione sobre cualquier variedad de Riemann de cualquier dimensión. De hecho, es una especialización de la mecánica Lagrangiana.

Esto se llama mecánica geométrica, como se describe en el libro de Calin & Chung, Mecánica Geométrica sobre Variedades de Riemann, en particular ver la sección 3.8 donde describen el Lagrangiano natural en tal variedad como la diferencia entre la energía cinética y potencial. También describen las formas de trabajo y momento y una expresión que relaciona el trabajo con el momento.

Luego en el teorema 3.20 dicen que una partícula en la variedad trazando un camino $c$ es un extremizador del Lagrangiano natural si verifica la 2da ley de movimiento de Newton en este contexto, es decir:

$F = \ddot{c} = \nabla_{\dot{c}} \dot{c}$

Aquí $F$ es la fuerza dada por $-\nabla V$ donde $V$ es algún potencial de energía en la variedad.

Por cierto, esto significa que la mecánica newtoniana funciona en coordenadas polares o en cualquier otro sistema de coordenadas.

Vale la pena señalar aquí que cuando la fuerza $F$ se anula, obtenemos la ecuación de una geodésica: una curva $c$ es una geodésica cuando:

$\ddot{c} = 0$

Así que tenemos el análogo de la primera ley de Newton en variedades de Riemann: cuando la fuerza sobre una partícula se anula entonces la partícula se mueve en una geodésica. Y cuando esta variedad es el espacio Euclídeo afín ordinario, estas son simplemente líneas rectas.

Todo lo anterior sigue siendo cierto para variedades semi-Riemannianas, en particular variedades Lorentzianas. Entonces, una forma de describir la ecuación geodésica en GR es decir que esta es la trayectoria seguida por una partícula en reposo donde una partícula está en reposo cuando no hay fuerza sobre ella. Por lo general, se dice que no hay marcos de reposo absolutos pero en este lenguaje existe, el marco de la luz o luxones (partículas sin masa).

Answer 3

Definitivamente tu profesor está incorrecto. De hecho, todo el punto $\vec{F}=m\vec{a}$ de escribirlo como una ecuación vectorial es enfatizar que la ecuación no depende del sistema de coordenadas que elijas para representar los vectores.

De hecho, vamos a desacreditar el contraejemplo de tu profesor verificando $\vec{F}=m\vec{a}$ en coordenadas cartesianas y polares. Supongamos que la partícula sigue la trayectoria descrita por tu profesor, sin pérdida de generalidad asumamos que la coordenada inicial $x$ es cero y la fuerza actuando sobre la partícula es cero en todo momento.

Sistema de Coordenadas Cartesianas

Primero escribamos la trayectoria en coordenadas cartesianas y verifiquemos que satisface la segunda ley de Newton.

El vector posición de la partícula es (Sin pérdida de generalidad, asumamos que la coordenada inicial $x$ es 0): \begin{align*} \vec{r} = vt \,\hat{x} + y_0 \hat{y} \end{align*} donde $y_0\neq 0$

Por lo tanto, al diferenciar directamente, se puede ver que $\vec{a} = \vec{0}$. Esto cumple con la segunda ley de Newton porque según $\vec{F} = m\vec{a}$, cuando $\vec{F}=0$, $\vec{a}=0$.

Sistema de Coordenadas Polares

¿Qué tal las coordenadas polares? Recordemos que en coordenadas polares, el vector unitario radial $\hat{r}$ siempre apunta a lo largo del vector de desplazamiento $\vec{r}$ y el vector unitario $\hat{\theta}$ se define como $\hat{r}$ rotado $90^o$ en sentido horario. ¿Entonces cómo se representa $\vec{r}$ en términos de las coordenadas polares? Muy simple, simplemente:

\begin{align*} \vec{r} = r \hat{r} \end{align*} donde $r=\sqrt{x^2 + y^2} = \sqrt{(vt)^2 + y_0^2}$

Entonces, ¿cuál es la velocidad de la partícula? \begin{align*} \vec{v} = \frac{d\vec{r}}{dt} = \frac{d}{dt} \left(r \hat{r}\right) = \frac{dr}{dt} \hat{r} + r\frac{d\hat{r}}{dt} \end{align*}

Aquí está la diferencia clave entre las coordenadas cartesianas y polares: En coordenadas cartesianas, el vector de base está fijo en el espacio, por lo tanto, el segundo término siempre es cero y simplemente necesitamos diferenciar la componente. Sin embargo, como puedes imaginar, en coordenadas polares, ¡el vector unitario $\hat{r}$ está cambiando de dirección a medida que se desplaza la partícula! Por lo tanto, tenemos términos adicionales en nuestras velocidades (en realidad, de manera similar para la aceleración).

Ahora, ¿cuál es la derivada temporal de $\hat{r}$ (y de manera similar $\hat{\theta}$ ya que tendremos ese término en la aceleración de todos modos)? La forma común de encontrarlo es primero convertir $\hat{r}$ y $\hat{\theta}$ en coordenadas cartesianas y tomar la derivada temporal. Sin embargo, dado que el razonamiento podría sonar circular al hacerlo, consideremos el problema geométricamente

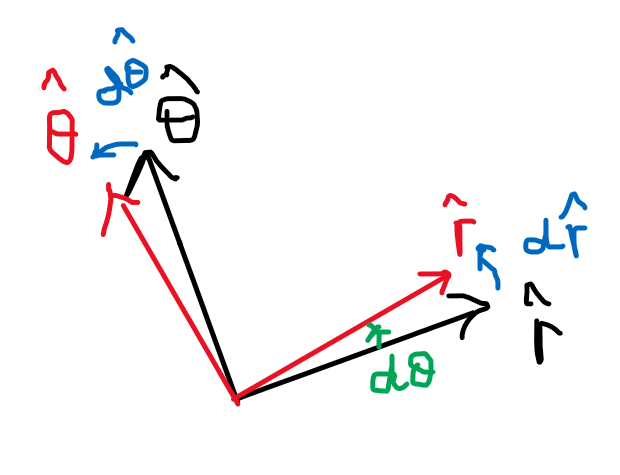
Primero, ¿cuándo cambiarán y cómo cambiarán $\hat{r}$ y $\hat{\theta}$? Bueno, un poco de imaginación nos dice que dado que $\hat{r},\hat{\theta}$ son ambos vectores unitarios, la única forma en que pueden cambiar es cuando rotan. Además, dado que $\hat{r}$ apunta en la misma dirección que $\vec{r}$ y $\hat{\theta}$ está "bloqueado" en relación a $\hat{r}$, sabemos que ambos solo cambiarán cuando el vector de desplazamiento rota alrededor del origen por algún ángulo $d\theta$.

Luego, consideremos la siguiente figura:

Como puedes ver, cuando $d\theta$ es pequeño, $d\hat{r}$ está en la dirección de $\hat{\theta}$ y $d\hat{\theta}$ está en la dirección de $-d\hat{r}$. Además, si $d\theta$ está en radianes, la longitud de estos vectores es $d\theta \times 1$ (es decir, la longitud de arco barrida por $\hat{r}$ y $\hat{\theta}$). Por lo tanto, obtenemos la siguiente ecuación:

\begin{align*} d\hat{r} &= d\theta \hat{\theta}\\ d\hat{\theta} &= -d\theta \hat{r} \end{align*}

Por lo tanto, dividiendo ambos lados por $dt$, tenemos: \begin{align*} \dot{\hat{r}} &= \dot{\theta}\hat{\theta}\\ \dot{\hat{\theta}} &= -\dot{\theta}\hat{r} \end{align*}

Usando estas ecuaciones y simplemente diferenciando $\vec{r}$, tendremos:

\begin{align*} \vec{v} &= \dot{r} \hat{r} + r\dot{\theta} \hat{\theta}\\ \vec{a} &= (\ddot{r} - r\dot{\theta}^2)\hat{r} + (r\ddot{\theta} + 2\dot{r} \dot{\theta}) \hat{\theta} \end{align*}

Ahora, ¿cuál es $\theta(t)$ y $r(t)$ en el ejemplo de tu profesor? Bueno, por definición: \begin{align*} r(t) &= \sqrt{x^2 + y^2} = \sqrt{(vt)^2 + y_0^2}\\ \theta(t) &= \arctan(y/x) = \arctan(y_0/vt) \end{align*}

Entonces simplemente tenemos:

\begin{align*} \dot{r} &= \frac{v^2 t}{r}\\ \ddot{r} &= \frac{v^2}{r} -\frac{(v^2 t)^2}{r^3}\\ \dot{\theta} &= -\frac{vy_0}{r^2}\\ \ddot{\theta} &= \frac{2 t v^3 y_0}{r^4} \end{align*}

Sustituyendo todo de nuevo en la fórmula de aceleración que derivamos: \begin{align*} \vec{a} = \left[\frac{v^2}{r} -\frac{(v^2 t)^2}{r^3} - r \left(-\frac{vy_0}{r^2}\right)^2\right] \hat{r} + \left[r\left(\frac{2 t v^3 y_0}{r^4}\right) +2\left(\frac{v^2 t}{r}\right)\left(-\frac{vy_0}{r^2}\right)\right] \hat{\theta} \end{align*}

Después de un poco de álgebra (puedes dejar que WolframAlpha haga el trabajo pesado) ambas componentes son $0$. Así que la aceleración medida en coordenadas polares es realmente 0, lo que concuerda con la ley de movimiento de Newton.

Answer 4

Este es un ejemplo de cómo los operadores no suelen conmutar en general. Es decir, si $x$ y $y$ son variables, $xy = yx$, pero si $f$ y $g$ son operadores, $fg$ generalmente no es igual a $gf$. Un operador es un conjunto de instrucciones sobre qué hacer con la expresión que le sigue. Consideremos un ejemplo simple con $f =$ "sumar 5" y $g =$ "multiplicar por 10". Entonces $fgx = 10x + 5$ y $gfx = 10x + 50$. Si queremos revertir los operadores, necesitamos un tercer operador que deshaga la consecuencia de la inversión del orden. Supongamos que empezamos con $gx$ y queremos operar en $x$ con $f$. En este caso, podríamos introducir $h =$ "restar 45". Entonces $fgx = hgfx$.

O podríamos introducir un operador que deshaga $g$, usando $g^{-1}$\= "dividir por 10". Luego podemos usar la identidad $gfg^{-1}gx = gfx$.

Aquí, "convertir de coordenadas cartesianas a polares" y "tomar la derivada temporal" son operadores. La mecánica de Newton está formulada en coordenadas cartesianas, así que si queremos aplicar la derivada temporal y obtener resultados newtonianos, necesitamos expresiones en coordenadas cartesianas o un tercer operador. Es decir: ya sea "convertir de polares a cartesianas" como $g^{-1}$ o "deshacer la consecuencia de operar 'convertir de cartesianas a polares' con 'tomar la derivada temporal'" como $h$.

Answer 5

Estas son las ecuaciones NEWTON en coordenadas cartesianas (tu caso)

$$m\,\ddot x=0\\ m\,\ddot y=0$$

y las condiciones iniciales $\dot x(0)=v_0~,\dot y(0)=0~$ y $~x(0)=0~,y(0)=y_0$

con :

$$x=r\,\cos(\phi)\tag 1$$ $$y=r\,\sin(\phi)\tag 2$$

trasladar las EOM's al espacio polar y obtener dos ecuaciones diferenciales $~\ddot r=\ldots~,\ddot\phi=\ldots$

también debes trasladar las condiciones iniciales

desde

$$x_0=0=r_0\,\cos(\phi_0)\\ y_0=r_0\,\sin(\phi_0)\quad\Rightarrow\\ r_0=y_0~,\phi_0=\pi/2$$

y desde $$\dot x=v_0=\sin(\phi_0)\,\dot r_0+r\,\cos(\phi_0)\,\dot\phi_0\\ \dot y=0=\cos(\phi_0)\,\dot r_0-r_0\,\sin(\phi_0)\,\dot\phi_0\quad\Rightarrow\\ \dot\phi_0=\frac{v_0}{y_0}~,\dot r_0=0$$

ahora puedes resolver las EOM's polares y obtener $~r(t)~,\phi(t)~$ y con las ecuaciones (1) ,(2) $~x(t)~,y(t)$

---

Solución general \begin{align*} &\text{vector de posición en espacio polar}\\ &\mathbf{R}=\begin{bmatrix} x \\ y \\ \end{bmatrix}= \left[ \begin {array}{c} r\cos\left( \phi \right) \\ r\sin\left( \phi \right) \end {array} \right]\\ &\text{las EOM's en espacio polar }\\\\ &m\,\mathbf{J}^T\,\mathbf J\,\mathbf{\ddot{q}}=\mathbf{J}^T\,(\mathbf{F}-m\,\mathbf{Z})\\ &\text{donde}\\ &\mathbf{{q}}=\begin{bmatrix} r \\ \phi \\ \end{bmatrix}\quad ,\mathbf{J}=\frac{\partial \mathbf R}{\partial \mathbf q} \quad, \mathbf{Z}= \frac{\partial \left(\mathbf{J}\,\mathbf{\dot{q}}\right)}{\partial \mathbf q}\,\mathbf{\dot{q}}\quad, \mathbf{F}=\begin{bmatrix} F_x(\mathbf q~,\mathbf{\dot{q}}) \\ F_x(\mathbf q~,\mathbf{\dot{q}}) \\ \end{bmatrix}\\\\ &\text{Transferir las condiciones iniciales} \\ & \begin{bmatrix} x_0 \\ y_0 \\ \end{bmatrix}= \left[ \begin {array}{c} r_0\cos \left( \phi_0 \right) \\ r_0\sin \left( \phi_0 \right) \end {array} \right]\quad\Rightarrow r_0~,\phi_0\\\\ & \begin{bmatrix} \dot x(0) \\ \dot y(0) \\ \end{bmatrix}= \mathbf{J}\,\mathbf{\dot{q}}\bigg|_{r_0~,\phi_0}\quad \Rightarrow\ \dot{r}(0)~,\dot{\phi}(0) \end{align*}

\begin{align*} &\text{tu ejemplo}\\\\ &\mathbf{J}=\left[ \begin {array}{cc} \cos \left( \phi \right) &-r\sin \left( \phi \right) \\ \sin \left( \phi \right) &r\cos \left( \phi \right) \end {array} \right] \\ &\mathbf{Z}= \left[ \begin {array}{c} -\dot\phi \, \left( 2\,\sin \left( \phi \right) {\dot{r}}+r\cos \left( \phi \right) \dot\phi \right) \\ \dot\phi \, \left( 2\,\cos \left( \phi \right) {\dot{r}}-r\sin \left( \phi \right) \dot\phi \right) \end {array} \right] \\ &\mathbf{F}=\mathbf{0}\\\\ &\text{EOM's}\\ &\ddot{r}-r\dot{\phi}^2=0\\ &\ddot{\phi}\,r+2\dot{\phi}\dot{r}=0\\ &\text{con las condiciones iniciales}\quad r(0)=y_0~,\dot{r}(0)=0~,\phi(0)=\frac{\pi}{2}~, \dot{\phi}(0)=-\frac{v_0}{y_0}\\ &obtienes la solución\\ &r(t)=\sqrt{y_0^2+v_0^2\,t^2}\\ &\phi(t)=\arctan\left(\frac{y_0}{r(t)},\frac{v_0\,t}{r(t)}\right)\\ &\Rightarrow\\ &\begin{bmatrix} x(t) \\ y(t) \\ \end{bmatrix}=r(t)\begin{bmatrix} \cos(\phi(t)) \\ \sin(\phi(t)) \\ \end{bmatrix}=\begin{bmatrix} v_0\,t \\ y_0 \\ \end{bmatrix} \end{align*}

obtienes la misma solución con coordenadas cartesianas

$$m\ddot x=0~,x(0)=0~,\dot x(0)=v_0\quad \Rightarrow x(t)=v_0\,t\\ m\ddot y=0~,y(0)=y_0~,\dot y(0)=0\quad \Rightarrow y(t)=y_0$$

conclusión

obtienes la misma solución en coordenadas cartesianas y coordenadas polares solo si puedes mapear las condiciones iniciales. esto sucede si

$$\det(\mathbf J)\bigg|_{r(0),\phi(0)}\ne 0$$

con $$\det(\mathbf J)=r\bigg|_{r(0)}\\ r(0)=\sqrt{x_0^2+y_0^2}$$ así que si $~x_0=0~$ y $~y_0=0~$ no puedes mapear las condiciones iniciales a coordenadas polares en este caso no puedes mapear las soluciones