¿Por qué las ondas viajeras continúan después de que la suma de la amplitud sea igual a 0?

Question

Mi profesor planteó una pregunta interesante al final de la última clase, pero no logro descifrar la respuesta. La pregunta es la siguiente (recordada de memoria):

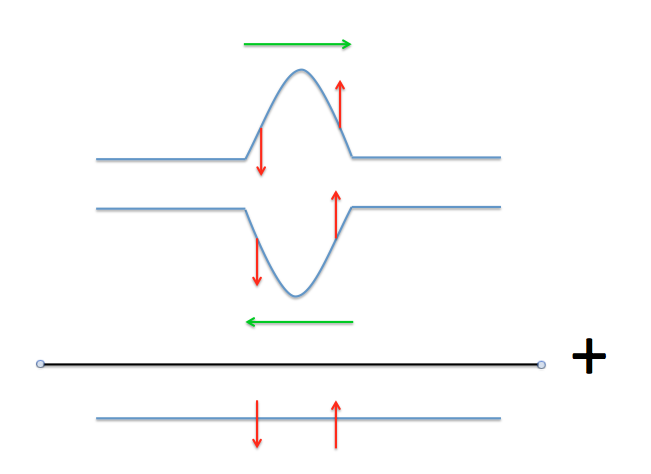
Hay dos pulsos de onda viajeros moviéndose en direcciones opuestas a lo largo de una cuerda con amplitudes iguales y opuestas. Luego, cuando los dos pulsos de onda se encuentran, interfieren destructivamente y por ese instante la cuerda queda plana. ¿Por qué continúan las ondas después de ese punto?

Aquí hay una imagen que encontré que ilustra el escenario

Sé que tiene que ver algo con las leyes de conservación, pero no he podido razonarlo. Según entiendo, las ondas se propagan porque la parte delantera de la onda está tirando de la parte de la cuerda que está delante de ella hacia arriba y la parte trasera de la onda está tirando hacia abajo y el efecto neto es un pulso que se propaga hacia adelante en la cuerda (¿es correcto?). Pero luego, para mí, eso significa que si la cuerda alguna vez está plana, entonces nada está tirando hacia otra cosa, por lo que la onda no debería comenzar de nuevo.

Desde una perspectiva de conservación, supongo que hay un exceso de energía en el sistema y eso es lo que mantiene las ondas en movimiento, pero entonces ¿dónde está esa energía extra cuando las ondas se anulan? ¿Se convierte simplemente en algún tipo de energía potencial?

¡Esta pregunta realmente es desconcertante! :\

Answer 1

Lo que no se puede ver dibujando la imagen es la velocidad de los puntos individuales de la cuerda. Incluso si la cuerda está plana en el momento de la "cancelación", la cuerda sigue moviéndose en ese instante. No deja de moverse solo porque parecía plana por un instante. Tu energía "extra" o "oculta" aquí es simplemente energía cinética.

Matemáticamente, la razón es que la ecuación de onda es de segundo orden, por lo tanto requiere tanto la posición momentánea de la cuerda como también la velocidad momentánea de cada punto en ella para producir una solución única.

Answer 2

La excelente descripción de ACuriousMind faltaba una imagen. ¡Aquí está:

Esto muestra claramente que para la onda que se mueve hacia la derecha, la parte delantera se mueve hacia arriba y la trasera hacia abajo. Para la onda opuesta que viaja hacia la izquierda, la parte delantera (ahora a la izquierda) se mueve hacia abajo y la trasera hacia arriba.

Sumándolas, obtienes una línea recta con una velocidad significativa.

Answer 3

Solo para complementar las otras respuestas excelentes, aquí hay una animación que muestra cómo se ven realmente dos pulsos de onda con amplitud opuesta al pasar uno al otro:

Se puede ver claramente que, en el instante en que la cuerda queda momentáneamente plana, no está estacionaria sino que se está moviendo bastante rápido, y por lo tanto no se mantendrá plana por mucho tiempo.

(Obviamente, la animación representa una cuerda idealizada con una propagación de ondas perfectamente lineal y cero dispersión, pero el mismo comportamiento cualitativo se puede observar en el mundo real, por ejemplo en un resorte flexible.)

Answer 4

Las tensiones y fuerzas todavía están presentes en las fibras de la cuerda y recrean las ondas. Si confinas firmemente y sólidamente estas fuerzas en un nodo, las ondas no podrían pasar a través del modo, sino que se reflejarían a cada lado del nodo (ahora un límite fijo) y se observaría un cambio de fase. ¿Solo estoy adivinando, podría estar equivocado?