Si he muestreado una señal utilizando métodos de muestreo adecuados (Nyquist, filtrado, etc.) ¿cómo relaciono la longitud de mi FFT con la resolución de frecuencia resultante que puedo obtener?
Por ejemplo, si tengo una onda senoidal de 2,000 Hz y otra de 1,999 Hz, ¿cómo determinaría la longitud de la FFT necesaria para diferenciar de manera precisa entre esas dos ondas?
Si conoces el rango de posibles frecuencias de entrada, y el rango es estrecho, puedes aplicar el submuestreo para reducir el número de muestras y el tiempo de cálculo de la FFT. Con 256 muestras y una frecuencia de muestreo de 256 Hz, obtienes la deseada resolución de 1 Hz y un ancho de banda libre de alias de 128 Hz.
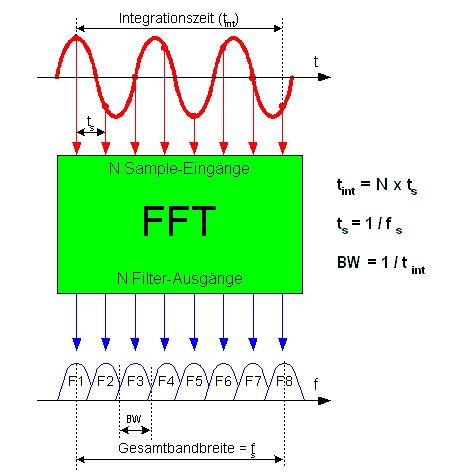
Creo que la última imagen es bastante clara, excepto por una corrección. El fondo de la imagen debería ser Fs/2 en lugar de Fs
Esta es mi experiencia con los cálculos de FFT en MATLAB:
si muestreas una onda senoidal a 8000 Hz durante 20 segundos, recogerás 8000x20= 160,000 muestras.
Cuando realizas el cálculo de la FFT, MATLAB creará una matriz de 160,000 filas y dos columnas. La primera columna será un arreglo de 0 a 4000Hz con pasos de 0.025 Hz (4000/160000) y la segunda columna será la densidad de potencia de esa frecuencia.
Así que la resolución en este caso será de 0.025 Hz y la resolución será:
Res = [Fs/2]/N
N= duración (s) x Fs (Hz)
\==> Res = (Fs/2)/(duración x Fs)= 1/(2 x Duración)
Así que para tu ejemplo, si deseas distinguir 2000 Hz de 1999 Hz, tu resolución debería ser al menos de 1 Hz (yo diría 0.5 Hz para un resultado más fiable)
Así que debes muestrear al menos a 4000Hz durante 1 segundo (4000 muestras) para obtener una resolución de 0.5 Hz y una duración de 0.5 segundos (2000 muestras) para obtener una resolución de 1 Hz.
Si fuera tú, aumentaría la duración a 5 segundos para obtener una resolución de 0.1 Hz. Con esta resolución, puedes distinguir fácilmente 1999Hz, 1999.1 Hz, 1999.2 Hz, etc.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
