Si una estrella que pasa puede empujar los cometas en la Nube de Oort, ¿por qué la Luna no perturba las órbitas de los satélites de alto vuelo?
¿O sí lo hace? ¿Quizás los satélites necesitan correcciones de curso periódicas?
Respuestas
¿Demasiados anuncios?
abligh
Puntos
191
La luna interrumpe absolutamente la órbita de un satélite geoestacionario. Así como la luna puede causar mareas en la superficie de la Tierra, la atracción gravitatoria de la luna en un satélite hará que comience a derivar ligeramente al norte/sur en su órbita. Los satélites geoestacionarios deben contrarrestar activamente esto si desean permanecer geoestacionarios.
Ver esta página para más información https://www.satsig.net//satellite/inclined-orbit-operation.htm
user283846
Puntos
116
La luna siempre "perturbará" la órbita hasta cierto punto, pero "disruptir" una órbita es sacar al satélite de órbita. Esto solo sucederá si la órbita es muy ancha, aproximadamente cuando llega al punto de Lagrange L1, ¡a unos 85% de la distancia de la Luna! Aquí hay un dibujo que muestra claramente órbitas estables y disruptivas: (reemplace el sistema Sol-Tierra con el sistema Tierra-Luna)
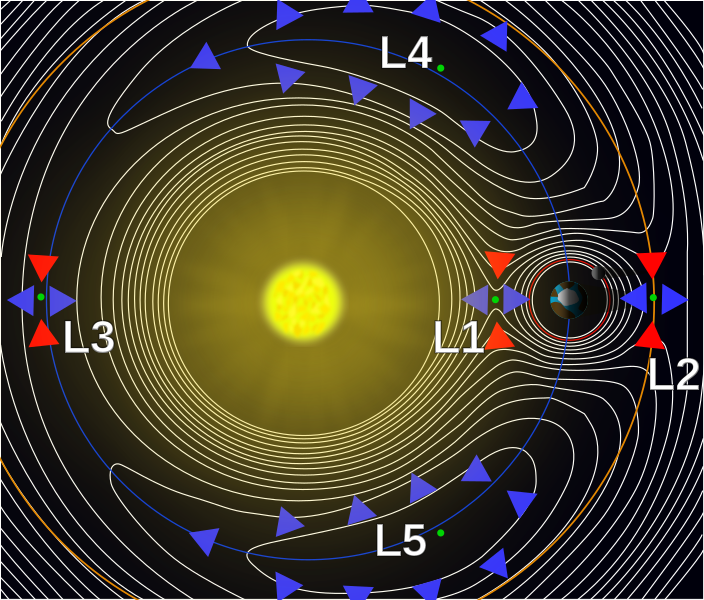https://en.wikipedia.org/wiki/Lagrange_point#/media/File:Lagrange_points2.svg
El dibujo también muestra que las cosas son mucho menos favorables para órbitas alrededor de una masa más pequeña, es decir, un satélite alrededor de la Luna en lugar de la Tierra. Más precisamente, la región alrededor de la Luna donde esas órbitas seguirían siendo estables es la llamada esfera de Hill: $$ R_H= (e-1) \ a \ \left(\frac{m_2}{m_1+m_2}\right)^{1/3} $$ pero con masas $m_1$ y $m_2$ para el sistema Tierra-Luna (y $e$ y $a$ la excentricidad y el semieje mayor) que da casi el mismo resultado que simplemente usando la posición L1.
Los satélites de vuelo más alto orbitan la tierra a una distancia de $42000$ km (la órbita geoestacionaria) lejos del centro de la tierra.
Recuerda que la fuerza gravitacional es $F\propto \frac{M}{r^2}$.
Por lo tanto, la fuerza de la luna (masa $M=7.3\cdot 10^{22}$ kg, distancia $r=380000$ km) sobre el satélite es mucho más pequeña que la fuerza de la tierra (masa $M=6.0\cdot 10^{24}$ kg, distancia $r=42000$ km) sobre el satélite. Usando estos números, encuentras que la fuerza ejercida por la luna es aproximadamente $10^{-4}$ veces más pequeña que la fuerza ejercida por la tierra. Por lo tanto, el efecto de la luna es demasiado pequeño para interrumpir significativamente la órbita del satélite alrededor de la tierra.
La situación es diferente cuando una estrella se mueve a través de la Nube de Oort. La estrella y el sol tienen masas similares, y están a distancias similares de los cometas. Por lo tanto, las fuerzas ejercidas por la estrella y el sol sobre un cometa serían de tamaño similar.
A G Foster
Puntos
7
La luna rebota por todos lados, nunca golpea el mismo apogeo o perigeo dos veces. Lo que ves publicado son solo promedios, y las cifras máximas y mínimas derivan de simulaciones computacionales que pueden predecir (hacia adelante y hacia atrás) alrededor de 5ky. A pesar de este caos, LLR (Lunar Laser Ranging) pretende medir la velocidad a la que la luna se aleja debido a la fuerza de marea, lo que debe requerir un considerable promedio y modelado a lo largo de muchos años.
El punto es que es mucho más fácil simular la atracción lunar en satélites que medir la tasa de alejamiento lunar.
