Forma correcta de computar la conductividad a partir de la fórmula de Kubo en superconductividad.

Question

Considera un Hamiltoniano completo $H=H_0 +H_1$ en una red con términos de salto $H_0$ de la forma $t c^* c$ e interacción atractiva $H_1= -V c^* c^* c c$ para que pueda ocurrir la superconductividad. Luego podemos aproximar $H$ con el Hamiltoniano de BCS cuasi-libre $H_\text{BCS}$ de la forma $\xi c^* c + \Delta^* cc+ \Delta c^* c^*$ donde $\xi, \Delta$ se pueden encontrar usando las ecuaciones de BdG.

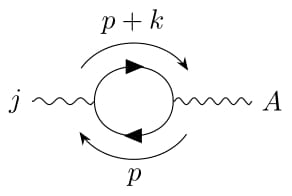
Para calcular la conductividad $\sigma$ de dicho sistema en el marco de la teoría de respuesta lineal (formalismo de Kubo), necesitamos calcular la correlación corriente-corriente $\chi_{ab}(t)$, dada por $$ \chi_{ab} (t) = -i\theta(t) \langle [J_a(t),J_b]\rangle $$

Puedo pensar en 2 formas de calcular $\chi_{ab}$. Una forma es aproximar la evolución temporal $J_a(t) =e^{iHt} J_a e^{-iHt}$ sustituyendo $H \mapsto H_\text{BCS}$ y de forma similar sustituir $\langle \cdots \rangle \mapsto \langle \cdots \rangle_{\text{BCS}}$. Otra forma sería calcular $\chi_{ab} (t)$ de forma perturbativa usando correcciones de un lazo, etc.

¿Cuál sería la forma "más correcta" de hacer estos cálculos? He visto a Schrieffer utilizar el primer método, pero también he visto artículos que utilizan el segundo. ¿Cuáles son algunas de las razones a favor de uno u otro?

EDICIÓN: Para ser más concreto, en las correcciones de un lazo, usamos $\langle\cdots \rangle \mapsto \langle \cdots \rangle_0$ y aplicamos el teorema de Wick basado en $\langle \cdots \rangle_0$. Me pregunto si podemos evitar el problema de calcular muchos diagramas simplemente calculando $$ \chi_{ab} (t) = -i\theta(t) \langle [e^{iH_\text{BCS} t} J_a e^{-iH_\text{BCS} t} ,J_b]\rangle_\text{BCS} $$

Answer 1

Intentemos proporcionar un esbozo de la derivación. Considera el metal normal, por lo que la interacción con un campo externo es $$H=\int d^3r\psi^{\dagger}\epsilon(p-eA)\psi,$$ donde $\epsilon$ es la ley de dispersión. Al realizar la variación con respecto a $A$, se encuentra la expresión para la corriente, $$j=e\psi^{\dagger}\nabla_p\epsilon(p)\psi-e^2\psi^{\dagger}\nabla_p[(A\nabla_p)\epsilon(p)]\psi. (*)$$ Para encontrar la contribución del primer término, debemos considerar $$H_{\text{int}}=-\int d^3j(r)A(r),$$ que es la aproximación de primer orden (en $A$),

y se puede calcular en términos de funciones de Green de Matsubara seguidas de una continuación analítica. El punto clave es que la expresión resultante tiene la forma (en el espacio de momentos) $$j(k)=Q(k)A(k),$$ donde para el metal normal la invariancia de calibre garantiza que $Q(0)=0$ (cf. $(*)$).

En el caso del superconductor, debemos considerar no solo promedios normales (como en el caso del metal normal) sino también anómalos. Esto significa que al realizar contracción de Wick, también se deben tener en cuenta las contracciones anómalas. Una derivación un poco tediosa dice que $Q(0)\neq 0$.

Finalmente, para mí parece que ambas derivaciones son iguales, porque la respuesta lineal no es más que una aproximación de 1 bucle.