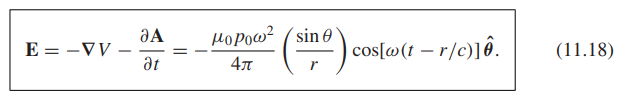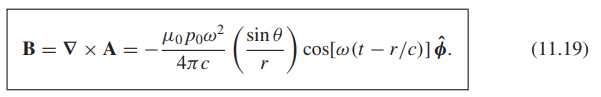¿Cómo puede una fuente puntual emitir ondas electromagnéticas esféricas cuando están prohibidas por las ecuaciones de Maxwell?

Question

Sé que existen soluciones de onda plana para las ecuaciones de Maxwell en el espacio libre, y traté de resolverlas para una onda esférica que emana de un punto pero no pude encontrar ninguna solución consistente con las 4 ecuaciones. Esto parece indicar que las ondas EM esféricas están generalmente prohibidas. Entonces, ¿por qué es que desde fuentes pequeñas (casi puntuales) como bombillas o estrellas vemos radiación EM esféricamente simétrica siendo liberada? ¿Y por qué podemos aplicar el principio de Huygens a las ondas EM que dice que cada punto en la onda actúa como una fuente de ondas esféricas pequeñas? Gracias por cualquier ayuda, es muy apreciada.

Answer 1

Estás en lo correcto: no existen ondas electromagnéticas esféricas. Una prueba alternativa es recurrir al teorema de la bola peluda. Si ponemos una superficie esférica alrededor de una fuente puntual, entonces el campo eléctrico en cada punto de la esfera es tangente a la esfera (ya que debe ser perpendicular a la dirección de propagación desde la fuente hasta el punto). El teorema de la bola peluda asegura que el campo eléctrico es cero en algún lugar de la esfera. Por lo tanto, para que el campo tenga la misma amplitud y fase en todas partes de la esfera, debe ser siempre cero en todas partes.

La razón por la que vemos fuentes de luz esféricamente simétricas en la vida real es porque esas fuentes son incoherentes. Tu cálculo y la prueba anterior solo descartan fuentes de luz simétricas esféricas coherentes. Es decir, una fuente con una única frecuencia fija de emisión no puede emitir de manera esféricamente simétrica. Pero la luz visible que sale de fuentes reales nunca es de una frecuencia fija. En alguna escala de tiempo (el tiempo de coherencia, aproximadamente $\tau=1/\Delta\nu$ donde $\Delta\nu$ es el ancho de banda), la fase de la onda de luz que sale de un punto fijo en un cuerpo emisor deriva aleatoriamente. Del mismo modo, en alguna escala de longitud (la longitud de coherencia $c\tau$), la fase de la luz emitida por diferentes puntos en el objeto varía aleatoriamente. Incluso si el campo EM real en un instante dado alrededor de un objeto nunca es esféricamente simétrico, la aleatoriedad (incoherencia) en la luz significa que cuando realizamos mediciones con dispositivos que promedian la intensidad de la luz sobre una gran área del objeto y tiempo (en comparación con la longitud y tiempo de coherencia), obtenemos algo esféricamente simétrico. Ten en cuenta que la intensidad promedio es un escalar, y por lo tanto no está sujeta al teorema de la bola peluda.

En frecuencias de radio, la situación es un poco diferente. Es fácil medir directamente campos eléctricos a esta frecuencia. También es mucho más fácil hacer fuentes de radio altamente coherentes. En el mundo de la radiofrecuencia, es un hecho básico y aceptado que no existe algo como una antena isotrópica. Siempre hay al menos un punto muerto en el patrón de emisión (por ejemplo, para una antena dipolo ordinaria, el punto muerto está a lo largo del eje de la antena). Eso es lo que motiva tecnologías como el formación de haces, que intenta cambiar dinámicamente el patrón de emisión dependiendo de dónde esté el objetivo para mejorar la recepción.

Es común en óptica usar la frase "onda esférica" para referirse a partes de una onda esférica. Por ejemplo, si haces pasar luz láser (que puede tener una larga longitud de coherencia) a través de una lente, puedes producir frentes de onda esféricos. Estos frentes de onda no son esferas completas, como lo prohíbe el teorema de la bola peluda. Más bien, son solo sectores de esferas. O, en otras palabras, la "fuente puntual coherente" que es la imagen del láser en la lente no emite en todas las direcciones, lo que hace posible su existencia. La descripción de la onda como esférica sigue siendo útil cuando lo único que nos importa es el campo en la región del espacio que está iluminado por el láser. Es decir, los frentes de onda pueden ser localmente esféricos, simplemente no globalmente.

Answer 2

El teorema de Birkhoff dice que la única solución esféricamente simétrica de las ecuaciones de Maxwell es el campo de una carga puntual estática, dado por el potencial de Coulomb. Sin embargo, cualquier cosa que aproxime la radiación esféricamente simétrica a un grado casi arbitrario está permitida (estoy escribiendo "casi" porque hay limitaciones físicas en la situación, pero no matemáticas). Tú mismo lo escribes: "fuentes casi puntiformes". Su radiación no es perfectamente esféricamente simétrica.

Answer 3

Debemos ser precisos con nuestras definiciones.

Una onda esférica con simetría esférica (los campos E y B dependen solo de r) es imposible, según el teorema de Birkhoff.

Sin embargo, las ondas esféricas se definen más naturalmente como ondas que se propagan esféricamente hacia fuera. En general, las ondas esféricas están en todas partes: uno esperaría que una configuración arbitraria de cargas irradian ondas que viajan hacia afuera a velocidad c. Sin embargo, el teorema citado implica cierta dependencia de $\phi$ y $\theta$ en los campos.

El libro de texto de Griffiths proporciona algunos ejemplos concretos. El autor comienza con una carga puntual que oscila hacia arriba y hacia abajo, y tiene un momento dipolar $p = p_0 \cos(\omega t)$. Luego aproxima y resuelve los campos E y B lejos de la fuente, y ignora los campos estáticos:

Si luego resolvemos el vector de Poynting (un vector que representa el flujo de energía) y promediamos en el tiempo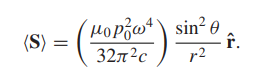

Esta onda viaja hacia afuera a velocidad c, con el flujo de energía disminuyendo por $1/r^2$, y el flujo de energía apuntando radialmente hacia afuera, exactamente como esperarías. Nota que las ondas no son simétricas esféricamente: los campos son menores cerca de los polos, y el flujo de energía depende de $\sin^2\theta$.

En realidad, esta no es una solución exacta de las ecuaciones de Maxwell debido a las aproximaciones, pero es muy cercana lejos de la fuente. Afortunadamente, Griffiths proporciona otro ejemplo de onda esférica que es una solución exacta (problema 9.35). Es bastante similar, tiene el mismo término $\sin^2\theta$ en el vector de Poynting.

Griffiths proporciona una aproximación general para una configuración arbitraria (dipolos rotativos, otros movimientos arbitrarios, etc.). También muestra que en general, cualquier carga puntual acelerada produce ondas esféricas que viajan hacia afuera a velocidad c.

Answer 4

Regarding the How.

La carga puntual solo puede emitir radiación electromagnética esférica o radiaciones de monopolo si la carga de esa partícula puntual cambia sin ninguna corriente entrante o saliente,

Supongamos una distribución de carga esférica y la carga en ella está cambiando en función del tiempo, el campo eléctrico en una capa arbitraria cambiará con el tiempo y cualquier carga lo sentirá, una radiación electromagnética esférica perfecta.

Pero esto no puede suceder ya que violaría el principio de conservación de la carga.

Answer 5

Debido a que se producen vastos números de fotones a la vez desde una fuente como una vela en todas direcciones en el espacio 3D, se forman ondas esféricas.