¿Por qué Roy Kerr afirma que el agujero negro de Kerr no contiene una singularidad?

Question

En un preprint publicado en arXiv, Roy Kerr afirma que hay un malentendido generalizado relacionado con la singularidad dentro del agujero negro que lleva su nombre.

• ¿Alguien puede explicar su argumento en "términos simples"?

• ¿Hay alguna falla en su razonamiento?

Aquí está el enlace al preprint: https://arxiv.org/abs/2312.00841

¿Los agujeros negros tienen singularidades?

R. P. Kerr

Resumen

No hay prueba de que los agujeros negros contengan singularidades cuando son generados por cuerpos físicos reales. Roger Penrose afirmó hace sesenta años que las superficies atrapadas llevan inevitablemente a rayos de luz de longitud afín finita (FALL's). Penrose y Stephen Hawking luego afirmaron que estos deben terminar en singularidades reales. Cuando no pudieron probar esto, lo decretaron como evidente. Se muestra que hay contraejemplos a través de cada punto en la métrica de Kerr. Estos son asintóticos al menos a un horizonte de eventos y no terminan en singularidades.

Aquí hay enlaces a charlas donde discutió estas ideas:

• https://youtu.be/8HuGElPH04s?si=B5-KdkY8EA3CON8v
• https://youtu.be/pccPAq7Ba8w?si=_tK6N9AeFnr9VlhZ

Answer 1

Por lo que puedo ver, el punto de Kerr es que el teorema de la singularidad no especifica si un objeto en colapso colapsará o no a una singularidad "real". Como recordatorio, los teoremas de singularidad suelen tener la forma

Dado un espacio-tiempo que cumple [algunas condiciones de causalidad] con [algunos conjuntos apropiados de condiciones de energía], el espacio-tiempo es incompleto en el sentido de tiempo/nulo

Existen muchos teoremas de este tipo, algunos sobre superficies atrapadas, algunos solo sobre el colapso de la materia en general, pero el punto de Kerr es que la noción de singularidad aquí es simplemente la incompletitud de curva de una singularidad, y no la noción más específica de una singularidad de curvatura.

Existen muchas definiciones de singularidad en la relatividad general que están vagamente conectadas entre sí, siendo la condición más general que un espacio-tiempo es singular si se da una curva inextensible con aceleración acotada, y al elegir algún punto, la longitud afín generalizada de esa curva desde ese punto hasta un extremo de la curva es finita. "Longitud afín generalizada" es una noción que pretende capturar la idea de finitud para una curva que incluye curvas nulas, ya que su longitud real siempre es cero.

Esta noción de singularidad se llama una $b$-singularity[1], la cual es la que utilizan los teoremas de Penrose[2] y lo que Kerr cuestiona, ya que estos son muy amplios e incluyen singularidades que no involucran la divergencia de la curvatura en absoluto, como los puntos de límite regulares, que son tan benignos que pueden ser eliminados considerando espacios-tiempo ligeramente más grandes, o singularidades cuasi-regulares[3][4], que tienen curvatura bien comportada pero no pueden ser eliminadas. Si un objeto viaja a lo largo de tal curva, no notará nada extraño en el camino antes de alcanzar la singularidad y simplemente dejará de existir.

La afirmación de Kerr es haber encontrado dos singularidades de este tipo. Su primer ejemplo es el del espacio-tiempo de Schwarzschild, donde fuera del agujero negro, un rayo de luz que se acerca asintóticamente al horizonte de eventos tiene una longitud finita, y nunca toca la singularidad, mientras que para el espacio-tiempo de Kerr, da un ejemplo de un rayo de luz que se mantiene entre el horizonte de eventos interno y externo que nunca desciende por debajo del horizonte de eventos interno y siempre tiene una longitud finita. Como la curvatura está acotada en ambos ejemplos que da (la curvatura siempre es menor que en el horizonte en esos ejemplos), no puede divergir y por lo tanto son a lo sumo cuasi-regulares.

Estos ejemplos no son suficientes por sí solos para desmentir lo que afirma, es decir, que los espacios-tiempo de esos tipos no tienen una singularidad de curvatura (esos espacios-tiempo también tienen una singularidad de curvatura), pero muestra de esta manera que los teoremas de singularidad por sí solos no son suficientes para demostrar que esto sucede sistemáticamente, ya que sigue siendo posible que las singularidades que ocurren durante los colapsos "reales" sean de este tipo. Sin restricciones del teorema de singularidad para tener la singularidad dentro del horizonte y solo las que están en el horizonte, podrían haber soluciones que sean como la métrica de Kerr en el exterior pero no tienen una singularidad en el interior, por ejemplo.

Por cierto, esta no es una observación completamente nueva, ya que Hawking lo mencionó él mismo en su artículo original sobre su teorema de la singularidad:

Pero el artículo de Kerr da un ejemplo de tal ocurrencia en ejemplos de espacio-tiempo bastante conocidos.

Editar: Algunas notas:

• Los tipos originales de singularidades del artículo de Penrose son en realidad $g$-singularidades (singularidades tales que la curva en cuestión es una geodésica), ya que la noción de singularidad $b$ surgió más tarde. Esto no cambia mucho el argumento.
• Aunque esas singularidades no son tales que las funciones de curvatura escalar divergen, no verifiqué si podrían ser singularidades no escalares (donde el tensor de Riemann evaluado a lo largo de un tetravector transportado paralelamente a lo largo de la curva no converge). Estas son bastante raras y como los componentes del tensor de Riemann en sí mismos no divergen, no pensé que podría ser relevante, pero los tetravectores mismos pueden divergir, ya que de hecho lo hacen para algunos campos tetraédricos en Schwarzschild, así que puede ser algo a tener en cuenta (estoy un poco suspicaz sobre su estatus como singularidades cuasi-regulares ya que no suelen ser de ese tipo en general y simplemente dependen de la topología y pueden ser extendidas localmente, lo cual no creo que funcionaría aquí, aunque la extensibilidad local es un concepto un tanto sospechoso).
• Esto se asemeja ligeramente a algún artículo de Penrose hablando sobre singularidades como puntos ideales y mencionando la existencia de $\infty$-TIP nulo-finits, los cuales son puntos ideales que están "en el infinito" según la perspectiva de una curva temporal, pero para los cuales las curvas nulas tienen una longitud afín finita, lo que él afirma solo puede ocurrir si la curvatura diverge, aunque sin muchos detalles.
• De acuerdo a otras respuestas, parece que cualquiera que sea la creencia de Kerr sobre la extensión adecuada del espacio-tiempo de Kerr, el ejemplo de Kerr que da es de hecho simplemente un punto de límite regular, que puede ser extendido, y por lo tanto no es gran cosa como singularidad.

Answer 2

El punto central del artículo de Kerr es mostrar ejemplos de geodésicas nulas inextensibles con longitud afín finita que no terminan en una singularidad. Para construir tal ejemplo, él examina geodésicas nulas a lo largo del eje de simetría del espaciotiempo de Kerr, en la región entre los horizontes interno y externo.

Tal curva cumplirá

$$ 0 = -dt^2 +dr^2 + \frac{2 m r}{r^2+a^2}(dr+dt)^2 ,$$

lo cual, como señala Kerr, tiene dos soluciones

$$ \frac{dr}{dt}=-1 \quad\text{and}\quad \frac{dr}{dt}=\frac{r^2-2mr+a^2}{r^2+2mr+a^2}.$$

Él etiqueta la primera como la solución "rápida", y la otra como "lenta". Es esta solución lenta la que él presenta como un ejemplo de una curva tipo luz de longitud afín finita que no termina en una singularidad. Como prueba de que no puede ser extendida, señala que $r^2-2mr+a^2$ es cero exactamente en los dos horizontes. Por lo tanto, para la solución "lenta", $\frac{dr}{dt}$ tiende a cero en los horizontes, y la solución debe asintotar al horizonte externo cuando $t\to-\infty$ y al horizonte interno cuando $t\to\infty$. Dado que $r$ es un parámetro afín para esta curva, esta porción de la curva tiene longitud afín finita.

Sin embargo, esta porción de la geodésica nula no es inextensible. La falla en la lógica de Kerr radica en que las coordenadas de Kerr (que él utiliza) no cubren la totalidad del espaciotiempo maximalmente extendido. Más precisamente, las coordenadas de Kerr son un tipo de coordenadas nulas entrantes, similares a las coordenadas de Eddington-Finkelstein entrantes para Schwarzschild. En el diagrama conforme (para $\theta=0$), las coordenadas de Kerr cubren las regiones sombreadas en verde. En el mismo diagrama, la línea azul muestra una curva nula "rápida", que pasa toda su longitud afín infinita en el parche de coordenadas de Kerr, y la línea roja muestra la curva nula "lenta". La porción sólida de la curva roja es la parte de longitud afín finita de esta curva. Como es evidente de inmediato, esta curva puede extenderse con la parte punteada para formar una curva de longitud afín infinita.

Entonces, el ejemplo de Kerr de una curva tipo luz de longitud afín finita que no puede extenderse y no termina en una singularidad, en realidad no lo es. La versión generalizada de esto presentada en su apéndice, sufre de la misma falla.

Answer 3

Hay algunas respuestas aquí que hacen un buen trabajo al exhibir las curvas que Kerr ha señalado, pero no creo que ninguna haya delineado su argumento central de manera fiel, y la mayoría ha pasado por alto observaciones clave en el corazón de su punto, por lo que me siento obligado a agregar algo un poco tarde. Si bien diría que la escritura de Kerr en este documento a veces es demasiado apasionada, excesivamente contraria, y lee un poco como un desahogo, su punto central tiene mucho más mérito y contenido de lo que algunas otras respuestas nos harían creer.

Punto de Kerr

Lo primero que hay que decir es que Kerr, por supuesto, no ha contradicho el teorema de Penrose (o variaciones del mismo debido a Hawking, etc.), y a pesar de su lenguaje bombástico, no creo que pretenda hacerlo. La declaración técnica y rigurosa del teorema que encontrarás en un libro de texto de RG (por ejemplo, Wald, O'Neill) es totalmente correcta. Además, Kerr no ha hecho ninguna observación trascendental; su punto esencial es algo que la mayoría de los relativistas dedicados que han estudiado los teoremas de singularidad han reconocido por sí mismos. Kerr ha observado con razón, sin embargo, que el teorema de Penrose a menudo es fuertemente sobreinterpretado en la comunidad de física en general.

El teorema de Penrose garantiza, bajo ciertas hipótesis, que el espacio-tiempo es nulogeodésicamente incompleto. En particular, establece que si un espacio-tiempo

(1) satisface la condición de energía nula,

(2) es globalmente hiperbólico con una hipersuperficie de Cauchy no compacta, y

(3) contiene una superficie atrapada,

entonces contiene al menos una geodésica nula incompleta, una trayectoria nulogeodésica que "termina temprano". Este teorema es un resultado hermoso que tuvo un gran impacto en la comunidad de RG, ya que estableció que la incompletitud no está ligada a las simetrías del espacio-tiempo. Aun así, Kerr ha señalado acertadamente que este resultado es en realidad mucho más débil de lo que a veces se le da crédito.

El punto principal del documento de Kerr es que este teorema no tiene nada que ver con la singularidad central de su espacio-tiempo homónimo. El teorema no nos dice que la singularidad de anillo está allí: la singularidad podría, en principio, ser excisada del espacio-tiempo y reemplazada por una distribución de materia estacionaria que se sostenga a sí misma sin contradecir el teorema de ninguna manera. El punto de discordia con las objeciones planteadas en algunas otras respuestas (y este punto no está bien planteado por Kerr, si es que pretendía hacerlo), es que la versión máximamente extendida del espacio-tiempo de Kerr no cumple con las hipótesis del teorema: la condición (2) no se cumple, ya que la extensión máxima no es globalmente hiperbólica. Esto significa que el teorema de Penrose no nos dice nada sobre la extensión máxima; en particular, no nos dice que la extensión máxima es nulogeodésicamente incompleta.

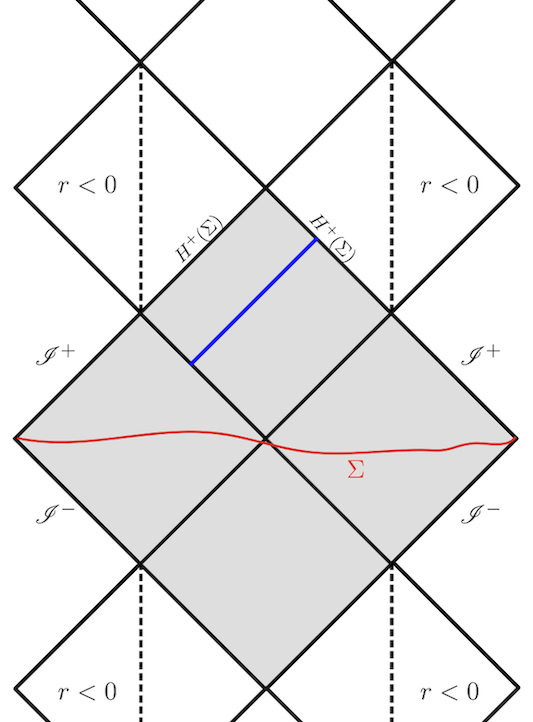
Para ilustrar, considera la siguiente parte del diagrama de Penrose de la sección transversal de $\theta = 0$ del espacio-tiempo de Kerr máximamente extendido.

$\hspace{3cm}$

La hipersuperficie roja $\Sigma$ corta la región exterior asintóticamente plana, y su desarrollo de Cauchy (la porción del espacio-tiempo determinada por $\Sigma$ a partir de la ecuación de Einstein del vacío) está sombreada en gris. El horizonte interno es el horizonte de Cauchy futuro $H^+(\Sigma)$ de $\Sigma$. Una de las curvas de ejemplo que Kerr ha identificado se muestra en azul.

La importancia de esta curva es que, dado que la extensión máxima completa no es globalmente hiperbólica, curvas como esta son todo lo que se puede obtener a partir del teorema de Penrose. De hecho, si uno restringe su atención a la región gris, este subconjunto es globalmente hiperbólico, y el teorema sí se aplica aquí: nos dice que la región gris es nulogeodésicamente incompleta como un espacio-tiempo en sí mismo. Por supuesto, que esta región sea incompleta no es nada nuevo ya que ya sabemos que podemos extender la métrica más allá de ella, y la incompletitud de la región gris no tiene nada que ver con cualquier comportamiento singular que pueda surgir más allá del horizonte de Cauchy bajo tal extensión. Dado que son incompletas en la región gris, las curvas de Kerr proporcionan ejemplos explícitos de las geodésicas nulas garantizadas por el teorema. Estas curvas, sin embargo, no demuestran ningún tipo de comportamiento singular: que sepamos que pueden extenderse en un espacio-tiempo más grande significa que no hay nada singular en ellas. Todos los escalares de curvatura son finitos, etc. Todo lo que nos dice el teorema de Penrose, entonces, es que curvas nulas como las de Kerr (que son decididamente no singulares) existen en la región gris, y son incompletas como geodésicas dentro de este conjunto globalmente hiperbólico. Tan pronto como se extiende el espacio-tiempo más allá de este subconjunto por cualquier cantidad que sea (quizás para tratar de incluir la singularidad de anillo), entonces el teorema de Penrose es simplemente inaplicable, diciéndonos nada sobre la extensión.

Por lo tanto, la conclusión es que el teorema de Penrose no ofrece ninguna prueba definitiva de que el interior de un agujero negro estacionario y axialmente simétrico debe ser singular: las geodésicas nulas incompletas que nos puede dar solo son incompletas como geodésicas restringidas a la región globalmente hiperbólica, y esta incompletitud no tiene nada que ver con la singularidad de anillo que pueda existir más allá del horizonte de Cauchy. Aunque Kerr no ha proporcionado explícitamente una extensión alternativa más allá del horizonte de Cauchy que sea no singular, no hay razón sólida para creer que no exista una. Nótese que la posibilidad de reemplazar la singularidad aquí no requiere en absoluto que se modele el colapso dinámico de una estrella giratoria; bien puede ser el caso que la singularidad de anillo pueda ser reemplazada por una distribución estacionaria de materia más allá del horizonte de Cauchy mientras se deja completamente inalterada la región gris.

La salvedad de la SCC

Una importante salvedad a la discusión anterior es que los horizontes de Cauchy generalmente se consideran inestables; esto se espera físicamente debido al desplazamiento al azul infinito de las señales de la materia en el exterior que un observador experimentaría al cruzar $H^+(\Sigma)$. Esta hipótesis se formaliza en la (no probada) Conjetura de Censura Cósmica Fuerte, que afirma que el desarrollo de Cauchy de datos iniciales físicos genéricos (por ejemplo, datos especificados en $\Sigma$) será inextensible a un espacio-tiempo más grande (físicamente significativo). Si uno acepta esto como verdadero, en nuestro diagrama significaría que perturbaciones arbitrariamente pequeñas a los datos iniciales de Kerr en $\Sigma$ esencialmente resultarían en que la extensión máxima completa colapsaría a solo la región gris. En este caso, cualquier curva incompleta como los ejemplos de Kerr terminarían de manera inextensible, un escenario que muchos relativistas llamarían fácilmente singular.

Incluso si se acepta la Censura Cósmica Fuerte, sin embargo, el teorema de Penrose sigue siendo bastante limitado. No garantiza que sus curvas nulas incompletas experimenten divergencia de curvatura, y aún no asegura que ninguna materia masiva, que sigue curvas temporales, coliapse a lo largo de trayectorias singulares.

Answer 4

Kerr escribe:

Las coordenadas originales de Kerr-Schild fueron elegidas deliberadamente para ser una generalización de las de Eddington, evitando así cualquier singularidad de coordenadas en cualquiera de los horizontes. Se demostrará en la Sección 5 que a través de cada punto de estos espacios hay rayos de luz que son asintóticamente tangentes a uno u otro horizonte, no tienen puntos finales y sin embargo sus longitudes afines son finitas.

[...]

El ejemplo más simple de un FALL [geodésica nula con longitud afín finita] [...] se encuentra en el eje de rotación entre los dos horizontes de eventos y es asintótica a cada uno de estos. Es lo que se obtiene cuando una linterna se ilumina "hacia atrás" mientras cae en un agujero negro por el eje. No cruza ninguno de los horizontes.

Claramente está hablando de geodésicas como la que se muestra en verde en este diagrama:

Este es un diagrama de Penrose del espacio-tiempo de Kerr máximo extendido con la parte cubierta por coordenadas de Kerr-Schild resaltada. La geodésica verde "termina" en el límite del parche de coordenadas solo en el sentido de que el resto no se puede describir utilizando esas coordenadas. Esto no es un contraejemplo a los teoremas de singularidad a menos que se interpreten de tal manera que sean trivialmente incorrectos. La geodésica verde no es "asintótica" a "los dos horizontes de eventos" (por los cuales se refiere a A y D); simplemente parece serlo en esas coordenadas particulares.

Él argumenta que los horizontes que no son A y D no son reales. De hecho, hay buenos argumentos que demuestran que no son reales, pero no respaldan su postura.

En el lado pasado, para describir un agujero negro realista que se forma a partir de una estrella colapsada, es necesario injertar una porción de la solución de Kerr al vacío en algún tipo de espacio-tiempo que describa la estrella. La porción que se utiliza no incluye el límite pasado del parche de Kerr-Schild (C y E) o cualquier cosa por debajo en el diagrama. Pero la geodésica no termina allí; continúa hacia el resto del espacio-tiempo, que simplemente no tiene forma de Kerr.

En el lado futuro, hay un argumento de que si la solución de Kerr se perturba ligeramente (por ejemplo, por la presencia de cualquier materia), entonces hay una singularidad de curvatura en A y B debido a la inestabilidad de inflación de masa.

Al juntar todos estos argumentos, es plausible que la única parte físicamente relevante del espacio-tiempo de Kerr sea (parte de) los cuadrados sombreados medio e inferior. Pero el argumento de Kerr es que la geodésica verde termina en una distancia afín finita sin singularidad, y eso simplemente no es cierto. En la dirección futura, termina en una singularidad. En la dirección pasada, se extiende a una distancia afín infinita hacia el universo previo al agujero negro (o al menos él no ha demostrado que no lo haga).

El borrador contiene algunas frases controversiales:

¿Por qué tantos creen que la estrella en su interior debe volverse singular en este momento? ¡Fe, no ciencia! ¡Sesenta años sin una prueba, pero ellos creen!.

(cursiva de él). Si es aceptado por una revista de renombre entonces supongo que estoy equivocado, pero creo que no lo será.

Answer 5

En pocas palabras, el Teorema de la Singularidad de Penrose afirma que la luz dentro del horizonte no puede escapar hasta el infinito, por lo que debe terminar en una singularidad. Esto significa que una singularidad debe existir dentro del horizonte.

Sin embargo, el espacio-tiempo de Kerr permite que la luz escape hasta el infinito en una región diferente, a menudo referida como "otro" o "universo paralelo". Bueno, si la luz dentro del horizonte puede escapar hasta el infinito (sin importar en qué región del espacio-tiempo), entonces no tiene que terminar en una singularidad. Esto significa que en general una singularidad no tiene que existir dentro del horizonte.

Este argumento no desacredita el Teorema de la Singularidad, solo indica que las condiciones requeridas por este teorema no se cumplen en todos los posibles tipos de espacio-tiempo.

Aparentemente, esta es la lógica en el abstracto. No he leído todo el artículo, pero quizás por "cuerpos físicos" Roy significa que todos los agujeros negros rotan, por lo que los espacios-tiempos estáticos tipo Schwarzschild sin escape no pueden existir en la realidad. Es solo una suposición, estoy seguro de que sus argumentos reales son mucho más inteligentes.