Conjetura: Dados cinco puntos, siempre podemos trazar un par de círculos no intersectantes cuyos extremos del diámetro son cuatro de esos puntos.

Question

¿La siguiente conjetura es verdadera o falsa?

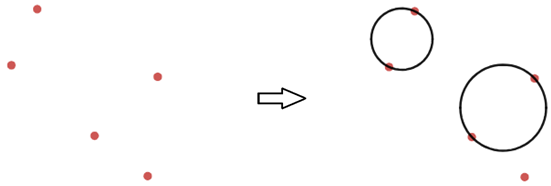
Dados cinco puntos coplanares, siempre podemos trazar al menos un par de círculos no intersectantes coplanares con los puntos, de modo que dos de los puntos dados sean los extremos del diámetro de un círculo, y otros dos de los puntos dados sean los extremos del diámetro del otro círculo.
Los círculos tangentes se consideran no intersectantes. Los círculos coincidentes se consideran intersectantes.

Ejemplo:

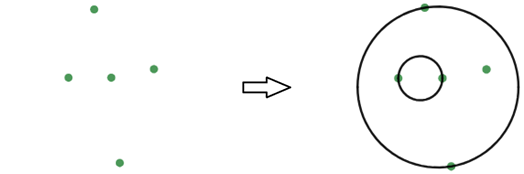
Otro ejemplo:

No puedo encontrar un contraejemplo, ni puedo probar la conjetura. He creado un generador de cinco puntos (pseudo)aleatorios.

(Si, en cambio, tuviéramos cuatro puntos, la conjetura no sería cierta: por ejemplo, si los cuatro puntos fueran los vértices de un triángulo equilátero más el centro, no podríamos trazar un par de círculos no intersectantes.)

Contexto: Estaba pensando en esta pregunta sobre puntos aleatorios en un disco. Mirando varios conjuntos de cinco puntos, se me ocurrió esta conjetura.

Editar: La conjetura generalizada ($2n+1$ puntos y $n$ círculos) no es verdadera.

Editar 2: He formulado, y respondido, una pregunta similar. Tal vez pueda proporcionar ideas para esta pregunta.

Editar 3 Publicado en MO.

Answer 1

Un contraejemplo se da por los siguientes cinco puntos: $$(0,0),(1,0), \Big(-\frac{64867}{77629},\frac{3389}{60094}\Big), \Big(\frac{5981}{56176},\frac{32211}{34172}\Big), \Big(\frac{5925}{117812},-\frac{103221}{116516}\Big).$$

---

Los cálculos y la forma en que se encontró este ejemplo se presentan en esta imagen pdf de un cuaderno de Mathematica. En particular, se señala que un cierto "defecto" de este ejemplo, que lo convierte en un contraejemplo, es muy pequeño, alrededor de $3\times10^{-6}$. Por lo tanto, aquí se pueden tener dos círculos "muy ligeramente intersectados", su intersección ciertamente invisible a simple vista si ambos círculos se muestran completamente.

Answer 2

Aquí hay una forma de convertirlo de geometría en álgebra sin raíces cuadradas. Tampoco tengo la solución.
Dado cuatro puntos $(a,b),(c,d)$ y $(e,f),(g,h)$, estamos buscando un punto $(x,y)$ en dos círculos, de modo que dos productos punto sean cero: $$ (x-a,y-b).(x-c,y-d)=0\\ (x-e,y-f).(x-g,y-h)=0 $$ La diferencia entre estos es lineal por lo que $(x,y)$ está en una línea recta y se puede parametrizar como $$ (x,y)=\left(\frac{eg-ac+t}{e+g-a-c},\frac{fh-bd-t}{f+h-b-d}\right) $$ donde $t$ es libre. Las dos ecuaciones al principio se convierten en un solo cuadrático en $t$, y el punto $(x,y)$ existe si el discriminante es no negativo.
El numerador que obtengo para el determinante es
$$ -4(eg-ac+fh-bd)^2+((a+c)(f+h)-(e+g)(b+d))^2 +4(e+g-a-c)(eg(e+g)-ac(a+c)) +4(f+h-b-d)(fh(f+h)-bd(b+d))\lt0 $$ Hay quince conjuntos de cuatro puntos emparejados. ¿Es posible mostrar que no todos los quince discriminantes pueden ser positivos?

Answer 3

Estas son solo algunas ideas,

Considere los dos puntos de manera que la distancia entre ellos sea máxima. En el diagrama, llamo a esos dos puntos $C$ y $B$, trabajaremos en el plano complejo con el origen como $O$, el punto medio de $CB$.

Hay un círculo azul especial dentro de mi diagrama, centrado en $O$ de tal manera que si tuviera un radio de $1$, entonces el círculo $BC$ tendría un radio de $\sqrt2$. (Escala en consecuencia)

Este círculo azul tiene la propiedad de que si dos puntos se encuentran dentro de este círculo, entonces el círculo formado por estos dos puntos necesariamente no se intersectará con el círculo $CB$.

Prueba: Considere cualquier dos puntos dentro o en el círculo unitario, llámelos $x,y$ Entonces el punto en el círculo formado por $xy$ que está más alejado del origen tiene magnitud: (1) $|(x+y)/2+i(x-y)/2|$ donde i es la unidad imaginaria. Luego, se aplica la desigualdad triangular:

$(1)\le(0.5)(|x||1+i|+|y||1-i|)\le 0.5(2\sqrt2)=\sqrt2$

Con esto, vemos que es necesario que como máximo 1 punto pueda estar dentro del círculo azul.

Luego intenté analizar 3 casos,

(1) Dos puntos están fuera del círculo $CB$.

(2) Un punto está fuera del círculo $CB$ y uno entre el círculo $CB$ y el círculo azul

(3) Dos puntos están entre el círculo $CB$ y el círculo azul.

Sugiero abordar el resto utilizando bashes complejos para las magnitudes.

Considere cualquier cuatro puntos complejos, $m,n,q,r$ . Luego, los círculos formados por $mn$ y $qr$ se intersectan necesariamente si

$|(m+n)/2-(q+r)/2|<|(m-n)/2|+|(q-r)/2|$
(Distancia entre los centros) < (La suma de los radios individuales)

Sé que esta afirmación no funciona cuando un círculo está contenido dentro de otro, por eso elegí que $CB$ sea el más grande ya que postulo que después del argumento anterior, no debería haber configuración de círculo dentro de círculo.

Progreso parcial, editaré si hay más avances.

Answer 4

EDICIÓN 2: Se ha proporcionado un contraejemplo excelente en otra respuesta, los cuatro puntos de los cuales son casi un cuadrado, lo que resulta en una "intersección muy ligera". Intenté encontrar uno comenzando desde un cuadrado pero fallé. Resulta que mi éxito final fue la idea de que "el ejemplo que está 'más cerca' de un contraejemplo son los cuatro puntos de un cuadrado junto con su centro".

---

EDICIÓN: La siguiente "prueba" es incorrecta, así que no te preocupes mucho por ella :P

Ahora creo que el ejemplo que está "más cerca" de un contraejemplo son los cuatro puntos de un cuadrado junto con su centro. En este caso, los círculos se intersecan entre sí o son tangentes. (Sin embargo, se considera que los círculos tangentes no se intersecan).

Dados cinco puntos, hay diez círculos. Podemos imaginar lo difícil que es hacer que se intersequen entre sí. No es difícil lidiar con los primeros cuatro puntos, pero el quinto punto introducirá cuatro círculos más y debemos considerar si cada uno de los cuatro se interseca o no con los seis círculos originales. (Entenderás mejor si intentas encontrar un ejemplo donde solo se permite que una pareja de círculos se intersequen entre sí).

---

Esto no es una prueba, solo proporciona algunas ideas.

Denota los cinco puntos como $A,B,C,D,E$. Supongamos que no son colineales, de lo contrario, la conclusión se cumple inmediatamente.

Primero elegimos $A,B$ de manera que tengan la distancia mínima. Sea $P$ el punto medio de $AB$.
Entre $C,D,E$ asumamos que $C$ es el que está más lejos de $P$. Luego podemos dibujar algunos círculos.
En la siguiente figura, los círculos rojos significan que $D,E$ deben estar fuera de ellos, ya que $AB$ es el más corto, los círculos verdes significan que $D,E$ deben estar dentro, ya que $C$ es el que está más lejos de $P$, y el anillo con líneas punteadas significa que $D$ debe estar dentro si queremos que el círculo con diámetro $CD$ se interseque con el que tiene diámetro $AB$.

Ahora supongamos que tanto $D,E$ están en el anillo. Podemos observar que solo quedan dos regiones pequeñas para ellos. De hecho, las regiones reales en las que el círculo($CD$ o $CE$) y el círculo($AB$) se intersecan son mucho más pequeñas, y una de ellas está aproximadamente dibujada en negro.
Si $D,E$ están en la misma región (por ejemplo, ambos en la región negra), entonces el círculo($DE$) no se interseca con el círculo $AB$. Si $D,E$ están en regiones diferentes, entonces el círculo($DE$) cubrirá el círculo($AB$).

Answer 5

Creo que encontré una prueba, que se basa en las siguientes dos afirmaciones:

1. Dado un conjunto de cinco puntos no colineales en el plano euclidiano, siempre es posible encontrar un subconjunto convexo de 4 puntos.

2. Dado un subconjunto convexo de 4 puntos en el plano euclidiano, siempre hay dos aristas opuestas cuyos puntos medios están separados por una distancia igual o mayor que el promedio de sus longitudes.

A partir de estas afirmaciones es posible realizar una demostración por construcción.

El caso restante con tres o más puntos colineales tiene una solución trivial eligiendo cualquier par de puntos en la línea y construyendo dos círculos, que necesariamente se tocarán en el punto común.

Esquema de la prueba del teorema 1: Consideremos tres puntos no colineales arbitrarios en el plano, (p,q,r). Añadimos un cuarto punto no colineal, s. Si s está fuera del triángulo (p,q,r) encontramos un cuadrilátero convexo (p,q,r,s). De lo contrario, hemos descompuesto el triángulo (p,q,r) en tres triángulos, (p,q,s), (q,r,s) y (p,r,s). Añadimos un quinto punto t. Si t está fuera del triángulo original (p,q,r), encontramos el cuadrilátero convexo (p,q,r,t). De lo contrario, t TIENE que estar dentro de uno de los triángulos más pequeños, digamos (p,q,s), lo que a su vez significa que está fuera de ambos (q,r,s) y (p,r,s), a partir de lo cual podemos construir el cuadrilátero convexo (q,r,s,t) o (p,r,s,t).