¿Qué método puedo usar para producir una única curva a partir de varias curvas?

Question

Estoy buscando un buen método para combinar un conjunto de curvas en una sola curva.

Esas curvas han sido producidas realizando una medición/prueba n veces bajo condiciones similares. Lo que estoy tratando de lograr es obtener una sola curva que represente estadísticamente la distribución más probable de puntos si realizo la misma prueba/medición la próxima vez.

¿Podría algún tipo de regresión lograr este objetivo?

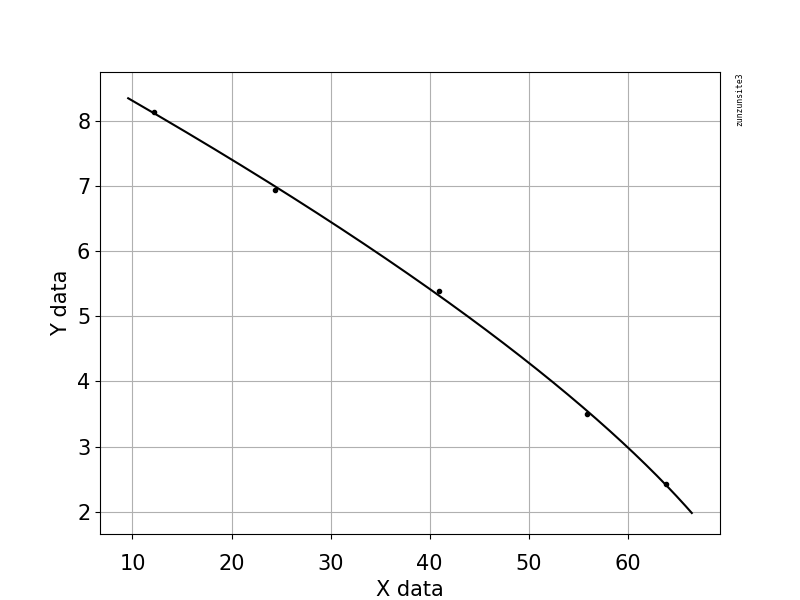
A continuación encontrará algunos datos de ejemplo para Q (caudal) y H (altura) para una bomba que rota a 1245 rpm. Por lo tanto, cada medición a rpm constante proporciona una curva para Q y H.

Q: 12,1557261    H: 8,1434835
Q: 24,3704478    H: 6,93492
Q: 40,9583469    H: 5,3908751
Q: 55,8666517    H: 3,4994621
Q: 63,8760173    H: 2,4220055

Answer 1

Encontré que la ecuación de densidad de rendimiento de Bleasdale, "1.0 / pow((a + b*x), (-1.0/c))", se ajustaba bien a tus datos de ejemplo con parámetros a = 2.6123446529575759E+01, b = -3.5195352662517970E-01 y c = 1.4724868235916486E+00 y si te gustaría probar otros conjuntos de datos, utilicé mi ajustador de curvas en línea de zunzun.com para esta ecuación específica en http://zunzun.com/Equation/2/YieldDensity/Bleasdale/ para realizar el ajuste. Personalmente creo que un ajuste de superficie del tipo "Q = f(H, RPM) podría ser más útil como una ecuación de propósito general, ya que una ecuación de superficie en 3D permitiría la selección del RPM óptimo - por eso había solicitado varias ejecuciones de datos, para poder buscar una ecuación de superficie en 3D simple. Aquí tienes un gráfico de mi ajuste para la ecuación de densidad de rendimiento de Bleasdale.