Hace unos meses, cuando estudiaba estrategias para la evaluación de programas funcionales, descubrí que el algoritmo óptimo utiliza algo llamado Combinadores de Interacción, un sistema de grafos basado en unos pocos nodos y reglas de reescritura .

He implementado y conseguido algunos resultados sorprendentes con él. Intenté aprender más, sólo para darme cuenta de que hay muy pocos artículos y casi nadie habla de ello. Otro día, por pura suerte, tropiezo con este documento sobre ordenadores químicos que serían "el futuro de la computación". A mitad de mi lectura, veo esto:

La similitud con las redes de interacción es sorprendente. Los nodos, las reglas, los puertos principales en el fondo, el sistema es prácticamente el mismo. Intenté buscar referencias para saber más sobre "eso", pero no encontré nada muy relevante, así que desistí. Otro día, por pura suerte una vez más, me encuentro con esta entrada del blog sobre algún tipo de álgebra lineal gráfica que "puede dividir por cero". A mitad de la lectura, veo esto:
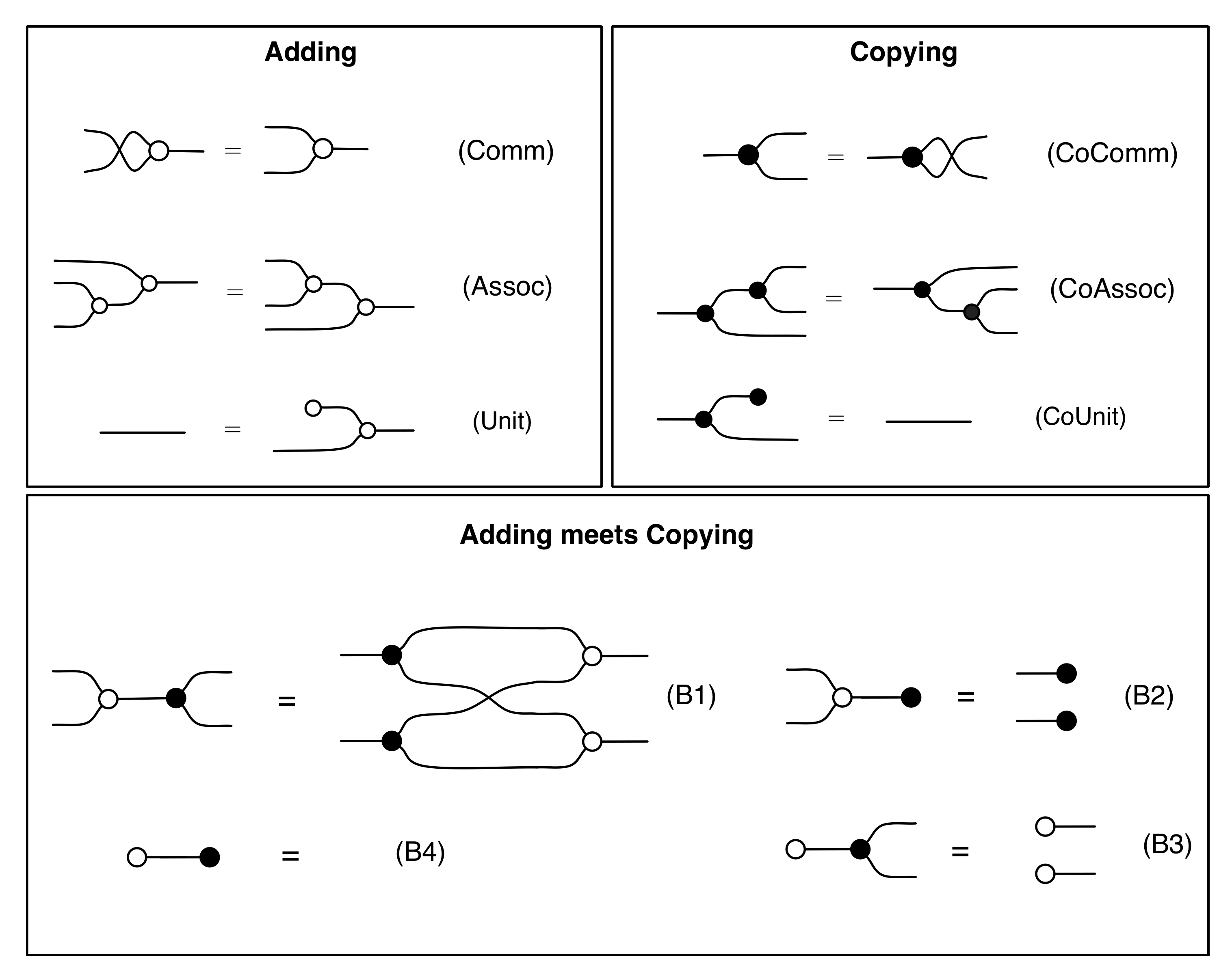
Una vez más, se puede ver la misma "cosa". Hay algunas pequeñas diferencias pero, en el fondo, es lo mismo. ¿Qué tienen en común esos sistemas? ¿Cómo se llama, cuál es su importancia, dónde se estudia y, lo más importante, por qué sigue apareciendo en campos completamente distintos?





