Sea $S$ sea una superficie convexa cerrada, el límite de una compacta convexo compacto en $\mathbb{R}^3$ . Me interesa saber si existen condiciones en su forma que garanticen que soporta una geodésica larga y simple (no autocruzada). La dirección longitud de una geodésica para mis propósitos es la distancia más larga geodésica antes de volver al punto de partida. de partida. Alguna condición es necesaria para el tipo de resultado que busco, para que todas las geodésicas de una esfera tengan la misma longitud.
Definir el elongación $L$ de $S$ como la mayor relación entre altura y diámetro mayor, $h/d$ de un cilindro de altura $h$ y diámetro $d$ en que $S$ está fuertemente inscrito. Por fuertemente inscrito Es decir que $S$ toca la parte superior, inferior y laterales del cilindro en de tal manera que ni la altura ni el diámetro puedan reducirse.
Podría utilizar un teorema de este tipo:
Si $S$ tiene alargamiento $L \ge k$ , geodésica en $S$ de longitud $\ge f(k)$ donde $f(k)$ i función creciente de $k$ por ejemplo, $c k$ para una constante $c > 0$ .
Tal vez tal teorema no pueda existir. ¿O tal vez exista un teorema de este tipo, pero sólo con ciertos supuestos de suavidad? Siempre hay al menos tres geodésicas cerradas en $S$ por un teorema de Lyusternik y Schnirelmann, pero quizás ¿podrían ser todas cortas?
Para un elipsoide, las tres geodésicas cerradas simples siguen los ejes mayor y menor, y la más larga de ellas satisface el tipo de relación que busco. (La elongación también podría definirse en términos de un elipsoide envolvente en lugar de un cilindro). Y un cilindro $S$ soporta una larga geodésica espiral:

Esas espirales son exactamente el tipo de geodésica que busco. Gracias por cualquier idea o sugerencia.
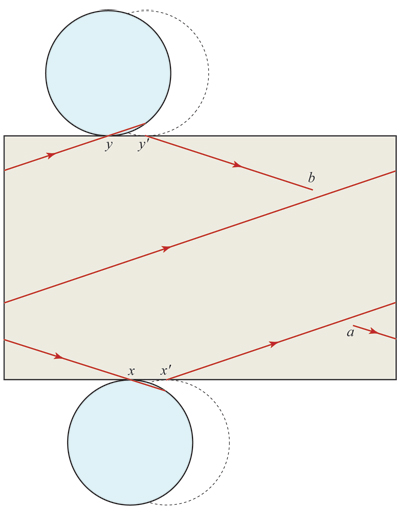
Editar . Puede que esto no aporte mucho, pero así es como yo veo una geodésica larga en un cilindro: empezando en $a$ , cruzando el fondo en un segmento $x x'$ , cruzando la parte superior en $y y'$ y parando en $b$ justo antes de que esté a punto de cruzarse.