Intervalos de confianza para la media utilizando una distribución t

Question

Un resumen de varios casos se da en la primera respuesta a la consulta:

Intervalo de confianza para la media - Distribución Normal o t de Student?

En el caso 3: datos Normales, varianza desconocida, se afirma que se debe usar la distribución t si la media y la desviación estándar de la población son desconocidas. Sin embargo, la definición de la distribución t requiere conocer la media poblacional (ya que t=($\bar{x}-\mu)/(S_x/\sqrt{N})$

¿Por qué se utiliza la distribución t para estimar la media poblacional (a través de intervalos de confianza) cuando la definición de la distribución t requiere que la media poblacional sea conocida?

Answer 1

El intervalo de confianza se da por $$\bar{x} - c_{\alpha,n} \bar{\sigma},\hat{x} + c_{\alpha,n} \hat{\sigma}$$ donde $c_{\alpha,n}$ es una constante que depende del tamaño de la muestra $n$ y del nivel de confianza $\alpha$.

La elección de este coeficiente $c_{\alpha,n}$ se basará en el conocimiento de que la diferencia de $\bar{x}$ de la verdadera media $\mu$ dividida por la estimación de la desviación estándar seguirá una distribución t.

Entonces esta cosa $\bar{x} - c_{\alpha,n} \hat{\sigma},\bar{x} + c_{\alpha,n} \hat{\sigma}$ es el intervalo de confianza. Su expresión de $t$ trata sobre la distribución de $\hat{x}$ en relación a $\mu$.

---

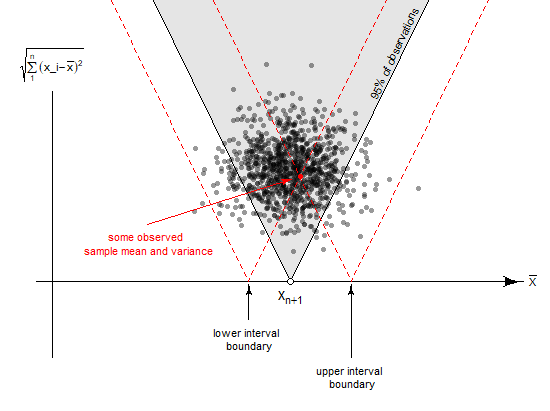
La imagen a continuación brinda una interpretación geométrica a la construcción del intervalo de confianza (esa imagen es de esta pregunta que se trata de un intervalo de predicción para $x_{n+1}$ pero es similar en el razonamiento con un intervalo de confianza para $\mu$)

En la imagen se observa la distribución de la muestra de la estimación de la media (eje x) y la estimación de la desviación estándar de la media (eje y). Las líneas diagonales muestran una región en la cual el 95% de las observaciones estarán. Si para una observación dada (representada en color rojo en la imagen) se elige un intervalo de confianza basado en esas mismas líneas diagonales al revés, entonces para el 95% de las observaciones se construirá un intervalo de confianza que contiene la media.

Esta construcción es independiente de la verdadera media $\mu$. Para una media diferente $\mu$ esta nube de observaciones se desplazará hacia la izquierda o hacia la derecha, pero el principio de la construcción del intervalo será el mismo. Todo es relativo a la verdadera media. La distribución para la diferencia de $\bar{x}-\mu$ es independiente de $\mu$.