Aplicación de la Ley de Gauss

Question

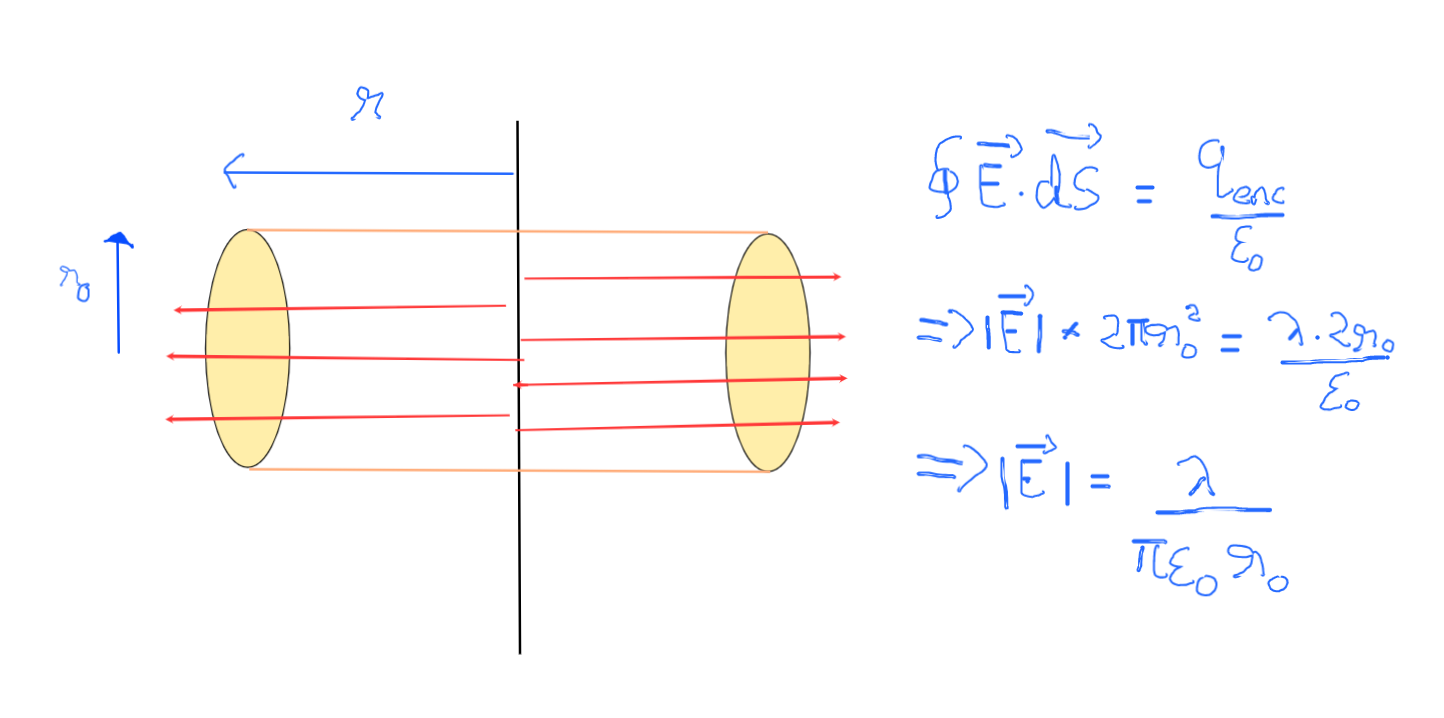
Estaba leyendo sobre el campo eléctrico a una distancia radial $r$ de un cable infinitamente largo y delgado con una densidad de carga lineal $\lambda$. Aunque entendí cómo se deriva utilizando la Ley de Gauss, estoy obteniendo un resultado diferente cuando se elige la Superficie Gaussiana de forma diferente. He adjuntado imágenes que muestran las Superficies Gaussianas elegidas en ambos casos, y cómo procedí a derivarlo. (Nota: solo he mostrado una parte del cable infinitamente largo en las imágenes siguientes). ¿Puede alguien decirme por qué la segunda derivación me está dando ese resultado?

La primera imagen muestra la derivación correcta, y la segunda imagen es la derivación que intenté, pero obtuve una respuesta diferente a la que esperaba.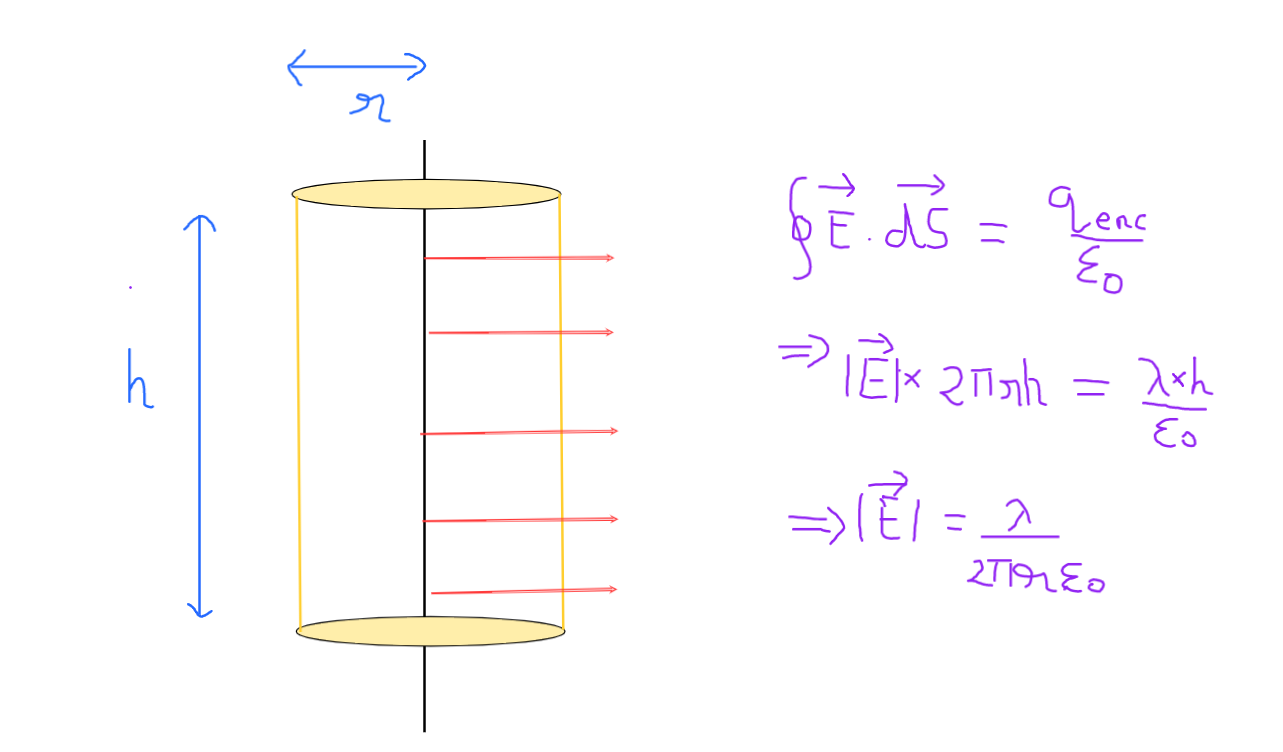

PD: Disculpen la escritura un poco ilegible, escribí con un ratón :)

Answer 1

Vuelve a pensar en qué dirección apuntan las líneas ${\bf E}$ del alambre largo. En el plano del papel, sí apuntan puramente hacia la izquierda y hacia la derecha. Sin embargo, ¿qué hay de las líneas que salen de la página? ¿En qué dirección apuntan y son perpendiculares a tu superficie gaussiana?

La razón por la que la primera funciona es porque en todos los puntos del cilindro, las líneas del campo ${\bf E}$ están o perfectamente perpendiculares a la superficie curva, o perfectamente paralelas al borde plano. En términos matemáticos, aquí ${\bf E}\cdot\text{d}{\bf S}=|{\bf E}||\text{d}{\bf S}|\text{ o }0$ solamente.

La segunda no funciona, porque ahora la mayoría de las líneas de campo (excepto por las pocas que has dibujado) están en ángulos extraños con respecto a tu superficie, y tendrías que hacer algún tipo de ponderación de componentes para obtener la respuesta correcta. En términos matemáticos, aquí ${\bf E}\cdot\text{d}{\bf S}\neq|{\bf E}||\text{d}{\bf S}|$ en general.