Siempre es una pena, por supuesto, cuando ninguno de los muchos paquetes LaTeX tiene precisamente el símbolo que podría utilizar en la pizarra. Al escribir, hay que intentar utilizar palabras siempre que sea posible, o al menos complementar los símbolos con palabras. Alguien que sólo lea las palabras debería ser capaz de captar los matices de su notación. Y, lo que es más importante, utilice la notación de forma coherente a lo largo de todo el documento.
Cuando hables en la pizarra, debes hablar todo lo que escribas, y escribir todo lo que hables, en el siguiente sentido: alguien ciego debe poder seguir la mayor parte de tu charla, y también alguien sordo debe poder seguir la mayor parte de la charla. Esto es importante incluso cuando se habla de tú a tú con otra persona. Así que escribe " $G \acts X$ " para su definición favorita de $\acts$ , pero tú hablas "Let $G$ actuar $X$ ." Y en los enunciados más importantes de la charla, es decir, los enunciados de definiciones y teoremas, debes escribir todas las palabras: "Sea $G$ actuar $X$ ."
Personalmente, me gusta alguna variación de tu opción 1. He visto la 3, y la utilizo en algunos apuntes de clase. No me gusta la 2: cuando la gente lee, tiende a dar mucha más importancia visual a la parte superior de las palabras y las letras que a la inferior (por eso casi todas las letras no cuelgan por debajo de la línea de base, sino que hay muchas que sobresalen más arriba, y casi se puede leer sólo con saber qué letras van más arriba). Así que pon la flecha arriba.

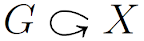




23 votos
No existe una notación estándar. Si me nombraran Emperador de la Notación, dictaría una variante girada 90 grados de tu tercera opción...
4 votos
Estoy bastante seguro de que los chicos de tex.stackexchange.com tendrían una solución LaTeX para lo que quieres.
13 votos
¿Qué hay de malo en "Que G actúe sobre X"?
2 votos
Relacionado: mathoverflow.net/questions/42929/sugerencias-para-una-buena-notacion/
2 votos
No creo que sea una pregunta interesante, pero me gusta la primera foto. :)
4 votos
Yo no soy un hablante nativo de Inglés y sólo recientemente, he aprendido el término "bikeshedding" (ver urbandictionary.com/define.php?term=piezasdebicicleta ), que es más o menos de lo que trata esta pregunta.
9 votos
@JackHuizenga: No tiene nada de malo, pero si escribo $f : X \to Y$ me preguntarás qué tiene de malo "Deja $f$ sea una función de $X$ a $Y$ "?