¿Cómo se puede explicar la vinculación en IF7 utilizando el método LCAO?

Question

Sé que la teoría VSEPR explica la estructura de $\ce{IF_7}$ (heptafluoruro de yodo) como una bipiramidal pentagonal. La teoría de enlace de valencia se puede usar para decir que tiene una hibridación $\mathrm{sp^3d^3}$ (creo). ¿Cómo se puede explicar la unión en él usando el método LCAO (Combinación lineal de orbitales atómicos) en la teoría de orbitales moleculares?

Tengo esta duda porque solo hay dos orbitales d "axiales" ($\mathrm{d}_{z^2}$ y $\mathrm{d}_{x^2-y^2}$) entre los 5 presentes, que pueden tener superposición frontal con orbitales p (los orbitales no axiales solo pueden tener superposición lateral). En el estado excitado, el átomo de yodo tiene 7 orbitales atómicos medio llenos (un orbital s, tres orbitales p y 3 orbitales d) y según LCAO cada uno debe combinarse con un orbital p de cada átomo de flor para formar orbitales moleculares por enlaces σ y π. Sin embargo, la formación de solo 6 enlaces σ puede ocurrir entre un átomo de yodo y 6 átomos de flor, ya que los enlaces σ involucran superposición frontal de orbitales, y solo hay 6 orbitales capaces de hacer eso (los orbitales s y p, y los dos orbitales d "axiales"). Por lo tanto, el séptimo átomo de flor debe estar en un enlace pπ-dπ con el fluoruro.

Esto no explica "cinco enlaces equivalentes y dos enlaces de longitud igual (todos enlaces σ)" como predice la teoría VSEPR. ¿Cuántos enlaces σ tiene en realidad?

Answer 1

No hay un enlace de 6-centro-10-electrones.

La situación de enlace en $\ce{IF7}$ se explica por Christe et al. (ver respuesta de ssavec) como un enlace de 6-centro-10-electrones. En el artículo en sí mismo, no encontré ninguna evidencia real que respalde esta afirmación y creo que es completamente incorrecta. La siguiente sección está tomada de Karl O. Christe, E. C. Curtis, David A. Dixon, J. Am. Chem. Soc. 1993, 115 (4), 1520–1526. y bien podría ser la culpable de esta monstruosidad.

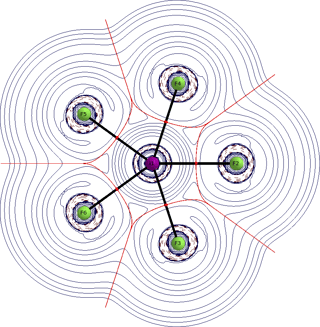
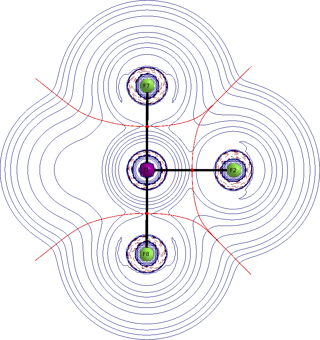
El enlace en el $\ce{XeF4}$ planar cuadrado se puede describir por dos enlaces semi-iónicos de 3-centros 4-electrones (3c-4e) para los cuatro enlaces $\ce{Xe-F}$ y dos pares de electrones valenciales solitarios en $\ce{Xe}$ (hibridaciones $\mathrm{s^2p}_z^2$). Los enlaces 3c-4e involucran a los orbitales $\mathrm{p}_x^2$ y $\mathrm{p}_y^2$ de xenón. La adición de un ion $\ce{F-}$ al plano ecuatorial en $\ce{XeF4}$ resulta en $\ce{XeF5-}$ pentagonal-planar y en la formación de un enlace semi-iónico de 6-centros 10-electrones (6c-10e) que involucra los orbitales híbridos $\mathrm{p}_x^2\mathrm{p}_y^2$ del $\ce{Xe}$ y seis electrones en los cinco ligandos de $\ce{F}$. Los dos pares de electrones valenciales solitarios en $\ce{Xe}$ en $\ce{XeF5-}$ son análogos a los de $\ce{XeF}$.
El fragmento planar $\ce{IF5}$ de $\ce{IF7}$ tiene esencialmente el mismo enlace que $\ce{XeF5-}$, como se muestra en los cálculos de población atómica dados en la Tabla VII. [...]

Continúan comparando las poblaciones de los orbitales de valencia en cuestión, sin indicar los métodos que utilizaron para determinarlo.

Los cálculos de la estructura electrónica se realizaron en los niveles ab initio de orbitales moleculares (MO) y de densidad funcional local (LDF). [...]

Una descripción más precisa del enlace en $\ce{IF7}$

El heptafluoruro de yodo es uno de los ejemplos clásicos cuando se trata de describir la hipervalencia y la expansión del octeto. Los intentos tempranos incluyeron los orbitales d en la descripción de ese fenómeno (VSEPR), resultando en una descripción que da la geometría correcta. Ahora sabemos que esta teoría está obsoleta y más a menudo es incorrecta que correcta.
Un problema fundamental en la descripción del enlace en esta molécula es asumir que está completamente covalentemente unido. Christe et al. reconocen que esto es incorrecto al afirmar que los enlaces son "semi-iónicos". Esto es - como veremos - ya algo forzado.

Un terminología más precisa para este tipo de moléculas es hiper-coordinado; es decir, el átomo central tiene un número de coordinación más alto que el común.

El análisis siguiente utiliza un cálculo en el nivel de teoría de la aproximación de densidad local. El conjunto de bases utilizado es de calidad triple zeta y emplea un pequeño potencial central efectivo para el yodo. La aproximación de ajuste de densidad se utilizó para acelerar un poco los cálculos. Esto se denota a menudo como DF-BP86/def2-TZVPP. El programa utilizado es Gaussian 09 rev. D.

Geometría

El rendimiento del método no es abrumador. Las longitudes de enlace son sobreestimadas por bastante. Como citado por Christe, se observa $r_\mathrm{obs}(\ce{I-F_{ax}})=178.1~\mathrm{pm}$ y $r_\mathrm{obs}(\ce{I-F_{eq}})=185.7~\mathrm{pm}$. Calculé $r_\mathrm{BP86}(\ce{I-F_{ax}})=190.4~\mathrm{pm}$ y $r_\mathrm{BP86}(\ce{I-F_{eq}})=195.6~\mathrm{pm}$. Otros métodos que todavía podría realizar razonablemente no lo hicieron mucho mejor. El resultado de MP2 es $r_\mathrm{MP2}(\ce{I-F_{ax}})=186.6~\mathrm{pm}$ y $r_\mathrm{MP2}(\ce{I-F_{eq}})=191.9~\mathrm{pm}.
Para el propósito del análisis, el método DFT debería ser suficiente. (También eché un vistazo a los otros resultados; no difieren significativamente.)

Teoría cuántica de átomos en moléculas (QTAIM)

Normalmente comenzaría mirando los orbitales, pero en este caso es más adecuado mirar la densidad electrónica en sí misma. Mejor aún, miramos el laplaciano de la densidad electrónica. Los gráficos de QTAIM representan la distribución del laplaciano dentro de la molécula. Las líneas azules sólidas indican agotamiento de carga $\nabla^2\rho>0$, las líneas rojas discontinuas indican acumulación de carga $\nabla^2\rho<0$, las esferas rojas son puntos críticos de enlace, las líneas negras sólidas son caminos de enlace, y las líneas rojas oscuro son superficies de flujo cero (estas separan los átomos). Ver una respuesta anterior mía para más información sobre QTAIM.
Tenemos dos puntos críticos de enlace para considerar, uno para el enlace axial y otro para el enlace ecuatorial. Encontramos valores bajos de densidad electrónica en ambos; $\rho(\ce{I-F_{eq}})=0.125~\mathrm{a.\!u.}$; $\rho(\ce{I-F_{ax}})=0.137~\mathrm{a.\!u.}$. El laplaciano en ambos puntos es positivo; $\nabla^2\rho(\ce{I-F_{eq}})=0.33~\mathrm{a.\!u.}$; $\nabla^2\rho(\ce{I-F_{ax}})=0.42~\mathrm{a.\!u.}$.
Estos valores indican predominantemente un enlace iónico. Los gráficos muestran claramente que los átomos aparecen como entidades separadas.
  
Con ese trasfondo parece incorrecto argumentar la situación de enlace formando enlaces covalentes, como se asume en la teoría de MO o VB.
Sin embargo, por incorrecto que sea descuidar el enlace iónico, es igualmente erróneo descuidar los enlaces covalentes.

Los Orbitales de $\ce{IF7}$

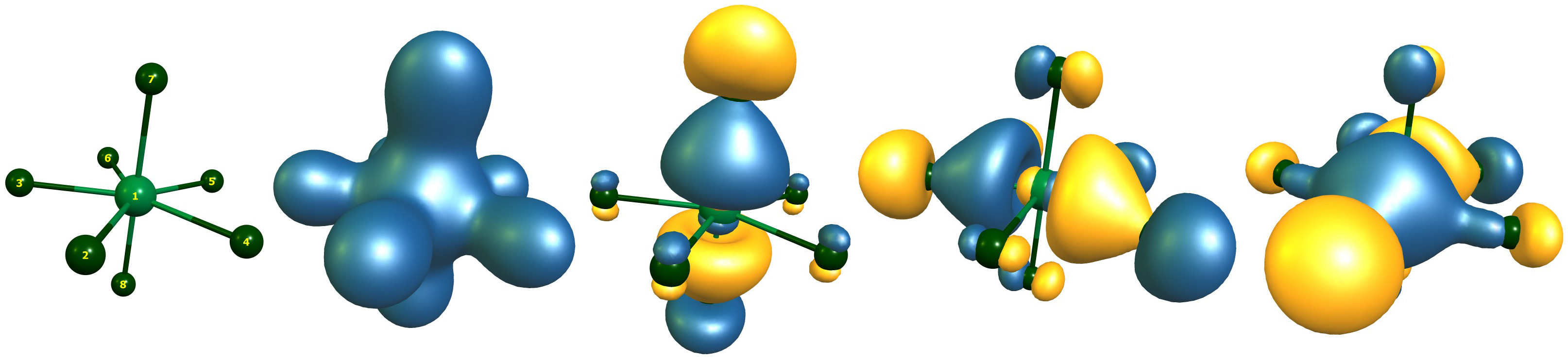
Hay un total de cuatro orbitales con aportes de yodo y flúor. No hay más de ocho electrones de enlace. No puedo imaginar que Christe et al. encontraron una solución diferente, ya que su nivel de teoría no era mejor (quizás peor). O bien no sabían cómo interpretar estos resultados o simplemente los pasaron por alto. Aquí están las líneas relevantes de la salida.

 Alpha occ 17 OE=-1.196 is I1-s=0.23 F7-s=0.18 F8-s=0.18
 Alpha occ 25 OE=-0.587 is I1-p=0.30 F7-p=0.28 F8-p=0.28
 Alpha occ 26 OE=-0.568 is I1-p=0.31 F4-p=0.19 F3-p=0.19
 Alpha occ 27 OE=-0.568 is I1-p=0.31 F2-p=0.21 F6-p=0.14 F5-p=0.14

(OE es el eigenvalor orbital en Hartree, las contribuciones que faltan de 1.00 están en los otros átomos, pero son demasiado pequeñas para desencadenar su impresión.)

En la imagen de enlace LCAO, tenemos un orbital de enlace totalmente simétrico de todos los átomos, un orbital que se refiere a los enlaces axiales, y dos orbitales degenerados para el plano ecuatorial.

Cargas e Índices de Enlace Wiberg

El carácter iónico de los enlaces también se puede ver en la distribución de carga. Mientras que el yodo tiene una carga positiva alta $q(\ce{I})=3.24$, los fluoros tienen una carga negativa $q(\ce{F})=-0.46$. Estas son cargas AIM calculadas con el paquete de programas MultiWFN.
El Análisis con orbitales de enlace naturales da un resultado similar, $q(\ce{I})=3.20$, $q(\ce{F})=-0.46`.br> Al observar la matriz de índices de enlace de Wiberg formada a partir de los orbitales atómicos naturales, encontramos un índice de enlace de $0.54` para los enlaces ecuatoriales y un valor ligeramente más alto de $0.56` para los enlaces axiales.

Conclusiones

No es posible determinar un número para cuántos enlaces sigma hay en la molécula, ya que esto es estrictamente posible solo para enlaces covalentes. Los enlaces aquí son predominantemente iónicos, con pequeñas contribuciones covalentes. El número de electrones de enlace no excede los ocho y por lo tanto cumple la regla del octeto.
VSEPR falla, como era de esperar. Se debe evitar el término hipervalencia y reemplazarlo por el término hiper-coordinación.

Answer 2

La estructura de $\ce{IF_7}$ no puede ser entendida como una simple bipirámide pentagonal estática. La explicación completa se encuentra en Karl O. Christe, E. C. Curtis, David A. Dixon, J. Am. Chem. Soc. 1993, 115 (4), 1520–1526.

La última oración del resumen describe claramente la situación de enlace: Sin embargo, estas características pueden ser explicadas mediante un esquema de enlace que involucra un híbrido pxy plano y delocalizado en el átomo central para la formación de cinco enlaces electroiónicos semicovalentes equatoriales de 6 centros y 10 electrones y un híbrido sp para la formación de dos enlaces axiales principalmente covalentes.