Cálculo de homotopías

Question

A menudo, en los libros estándar de topología algebraica (May, Switzer, Whithead, por ejemplo), hay pequeñas pruebas complicadas que dependen de demostrar que dos mapas son homotópicos. Esto es comparable a la forma en que construimos homotopías, elevaciones, etc. combinatoriamente en la teoría simplicial de la homotopía, pero por alguna razón nunca adquirí la habilidad (¿tal vez la intuición?) para llegar a estas homotopías en el caso topológico. Me desconcierta cómo se sacan estas fórmulas de la nada.

¿Me estoy perdiendo alguna técnica clave que suele enseñarse al principio de un curso de topología algebraica? ¿Es difícil incluso con la práctica? ¿Ha habido algún artículo que se centre en formas sistemáticas de generar estas cosas?

También me he dado cuenta de que en el libro de May, a menudo escribe fórmulas explícitas para sus homotopías, a veces de un modo que oscurece la cuestión en cuestión (por ejemplo, hay una homotopía que se describe mediante una fórmula explícita, pero no es más que un "representante de la homotopía natural" explícito entre el mapa de identidad y el mapa constante en un espacio de base contráctil). ¿Con qué frecuencia pueden sustituirse estas fórmulas aparentemente arbitrarias por descripciones más canónicas? (Esta última pregunta es suave para las personas con experiencia en topología)

Answer 1

El fenómeno básico es que a menudo la mejor manera de pensar en "pequeñas homotopías" es utilizar las partes geométricas de tu cerebro --- utilizar principalmente tu GPU (unidad de procesamiento de geometría), con la unidad de procesamiento aritmético, la unidad de procesamiento lógico y las unidades de procesamiento léxico en segundo plano, por así decirlo. Sin embargo, a la hora de escribir una demostración, es habitual, y normalmente más fácil, transcribirla en forma simbólica. Suele ser un proceso unidireccional: es mucho más difícil partir de fórmulas simbólicas y regenerar la intuición geométrica que partir de la intuición geométrica y transcribirla a fórmulas simbólicas.

Ahora es mucho más fácil crear figuras razonables que ilustren ideas geométricas que antes (hace 20 o 30 años, por ejemplo), pero sigue siendo difícil. Es especialmente difícil transmitir directamente la intuición geométrica en dimensiones superiores: los retratos de ideas geométricas con palabras pueden ser buenos, pero la mayoría de los escritos matemáticos los descuidan.

Creo que la mejor estrategia para aprender es evite leer las definiciones simbólicas de estas pequeñas homotopías hasta has dedicado algún esfuerzo a pensar en ellos por ti mismo, principalmente en tu cabeza. (Los bocetos también pueden ser buenos, pero a menudo suponen otra capa de dificultad. La imaginación geométrica no es predominantemente visual. habilidad ser capaz de dibujar una imagen en papel que represente adecuadamente un modelo mental geométrico).

Según mi experiencia, las descripciones simbólicas suelen interferir activamente en la comprensión geométrica; al principio, utilízalas sólo como pistas, para cuando hayas pensado mucho y estés atascado. Se necesita tiempo y concentración para construir buenas imágenes mentales, pero la imaginación geométrica mejora con la práctica, y merece la pena el esfuerzo. Con el tiempo, aprenderás a leer las fórmulas y evocar las imágenes geométricas.

Answer 2

A veces las imágenes geométricas fáciles tienen descripciones algebraicas que parecen incómodas. En las páginas 6 y 7 de Conciso di ejemplos en los que daba una imagen geométrica como fórmulas explícitas para aclarar la idea de dicha traslación. En otros casos (como en la equivalencia de homotopía de cofibras) simplemente encontré rápido y fácil escribir las homotopías (en términos de otras homotopías). A veces es demasiado laborioso dibujar las figuras, otras veces es demasiado laborioso escribir las homotopías. Hay que aprender a ser felizmente ecléctico y absorber todas las técnicas disponibles.

Añadido por PLC en la segunda frase anterior, el profesor May se refiere a su texto Curso conciso de topología algebraica . (Cuando me dio el curso, el título del borrador que nos entregó era Un curso rápido... (pero supongo que a los editores no les gustó mucho).

Answer 3

Harry, la expresión "un representante explícito de la homotopía natural entre el mapa identidad y el mapa constante en un espacio de base contractible" no me dice nada. Las homotopías no tienen "representantes", y un espacio contractible no tiene una homotopía "natural" entre la identidad y un mapa constante. ¿Supongo que te refieres a que May podría haber completado su demostración utilizando la existencia de alguna homotopía, sin nombrar realmente una en particular? O algo parecido.

Yo diría que cuando necesito hacer una homotopía, la mayoría de las veces o bien la hago moviéndome en línea recta o bien la hago a partir de otra homotopía. Una respuesta suave a una pregunta suave.

Answer 4

Según mi experiencia, la gran mayoría de las homotopías proceden de alguna combinación de (1) homotopías garantizadas por cofibraciones o fibraciones y (2) homotopías rectilíneas.

Por ejemplo, una aproximación estándar a la aproximación celular reduce al caso de un mapa de una célula a $X \cup D^n$ y, a continuación, utiliza la estructura lineal en el interior de $D^n$ para dar sentido a las homotopías rectilíneas.

Answer 5

@Harry Gindi: Tuve el mismo problema en los años 60 al escribir la primera edición de 1968 de mi libro ahora Topología y Groupoides . Luego estuve mirando artículos de Puppe, y descubrí que no tenía ni idea de cómo construir algunas de sus homotopías "diagramáticas". con fórmulas diferentes en cada bit. Esto fue parte de la motivación para encontrar el teorema de encolado para equivalencias de homotopía, que ahora es un resultado estándar en homotopía abstracta. Mi responder a otra pregunta ilustra cómo se obtiene por los métodos allí homotopías explícitas.

El uso de los grupoides dobles en la teoría de la homotopía obedecía a la misma motivación. Utilizando el grupoide doble definido aquí se puede enriquecer la categoría de espacios de Hausdorff sobre la categoría de estos grupoides dobles con conexión (aunque esto no se ha escrito en detalle) y esto se puede aplicar para construir homotopías. Para algunos cálculos en los grupoides dobles con conexiones, véase el capítulo 6 de Topología algebraica noabeliana sobre todo en las rotaciones (p.169).

También se puede enriquecer la categoría de espacios filtrados sobre la categoría cerrada monoidal simétrica de complejos cruzados, lo que permite de nuevo el cálculo de homotopías. Como se dice en la p.322 de Topología algebraica noabeliana (pdf disponible), esto requiere un estudio más detallado.

No estoy seguro de que el trabajo sobre categorías de modelos ayude tan directamente al cálculo de homotopías, a menos que se utilice explícitamente el objeto cilindro. El uso de homotopías es fundamental para Teoría de la Perturbación Homológica y se utilizan en la obra de Graham Ellis Programas de álgebra homológica en particular para construir resoluciones por inducción con una homotopía contratante.

Este papel utiliza groupoides de homotopía superior para discutir los corchetes de Toda.

Mi propio trabajo ha utilizado en gran medida métodos cúbicos como base para conjeturas y pruebas, debido a la facilidad para describir composiciones múltiples y homotopías.

Junio, 2014 Recuerdo un comentario de Raoul Bott que escuché por casualidad en la ICM de 1958: "¡Grothendieck estaba dispuesto a trabajar muy duro para hacer las cosas tautológicas!"

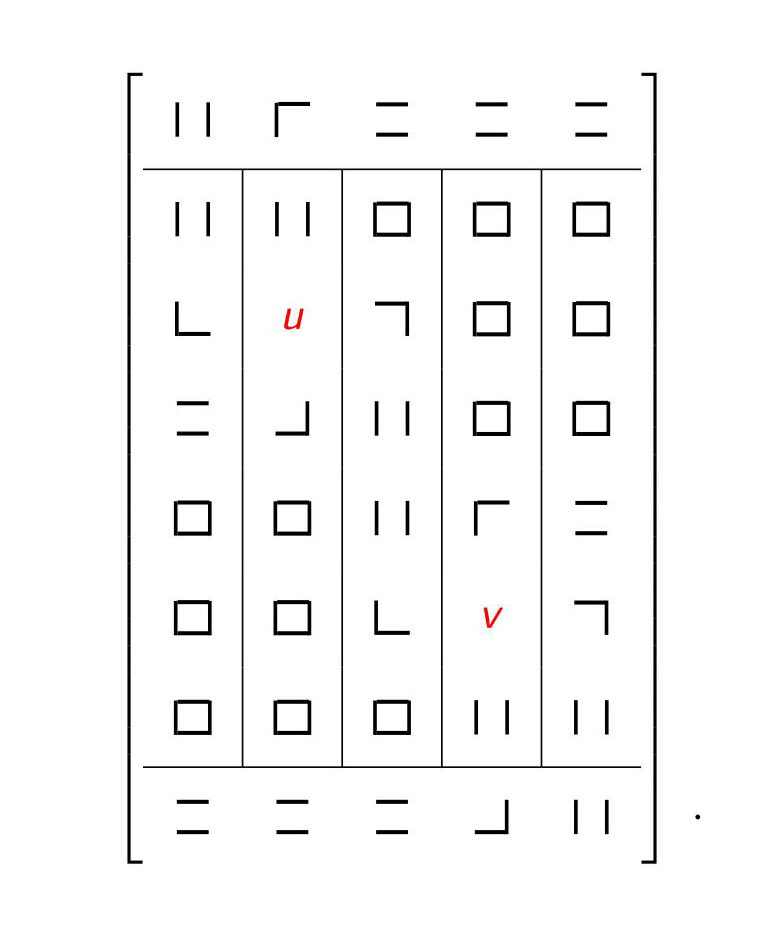
Marzo de 2016 La siguiente imagen

forma parte del argumento para demostrar una fórmula $\sigma (u +_2 v)= \sigma u +_1 \sigma v$ donde $u,v$ son clases de homotopía rel vértices de mapas $I^2 \to X$ que llevan las aristas a un subespacio $A$ y los vértices a un conjunto $C$ de puntos base, $+_1, +_2$ denotan respectivamente las composiciones en las direcciones vertical y horizontal, y $\sigma$ es lo que se denomina una "rotación". El diagrama se reinterpreta utilizando la ley y las reglas de intercambio entre los símbolos peculiares denominados "conexiones". La fórmula implica la existencia de una homotopía y en principio la da explícitamente, pero eso sería muy difícil de escribir en términos del tipo habitual de fórmulas.