Perpetuum Mobile

Question

En 2 horas después de publicar esto, me di cuenta de que preservar la medida de Liouville resuelve el problema por completo. Perdón por molestar...

---

Construcción de perpetuum mobile: Consideremos una habitación con paredes de espejo formada por dos arcos de dos elipses con focos comunes y dos segmentos de una perpendicular bisectriz para los focos como en la figura:

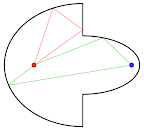
Coloca cuerpos de un punto con la misma temperatura en cada foco --- irradian y

• Todos los rayos del foco azul llegan al rojo.

• Gran parte de los rayos procedentes del foco rojo vuelven a él (son todos los rayos que se reflejan en la bisectriz), mientras que el resto se dirige al foco azul.

Así, el foco rojo se calienta más que el azul; es decir, tenemos un máquina de movimiento perpetuo de segundo tipo ...

Preguntas:

• ¿Por qué exactamente no funciona? Mi conjetura es: si en lugar de un punto-cuerpos que tenemos cuerpos con tamaño real (no importa cuán pequeño) ya no funcionará, pero soy demasiado perezoso para hacer cálculos, y yo también debe ser una buena explicación (sin cálculos).

• Para los que piensen que no son matemáticas, he aquí la formulación matemática: Supongamos que en lugar de cuerpos de un punto tenemos cuerpos muy pequeños de forma arbitraria. Entonces la física nos dice que ya no debería funcionar. PERO no veo prueba matemática de ello...

Comentario:

• Conozco esta construcción por Vladimir Troitsky. Una construcción similar (pero no tan elegante) aparece en un comentario sobre el Brain Teaser en el número de septiembre de 1972 de Physics Education (página 414). (¿tal vez antes?) --- gracias a Scott Carnahan por la referencia. En la página 446, hay una "solución", sólo dice que "no funcionaría debido a los tamaños finitos de [los cuerpos]" . Al año siguiente (junio de 1973, p.292) se publicó en la misma revista una carta con una explicación mejor, esta "explicación mejor" dice a grandes rasgos que no funciona por una "ley bien establecida".

Answer 1

Esto no es una respuesta, sino un comentario. Simplemente no encajaba.

¿Soy el único al que la clasificación del perpetuum mobili en tres tipos le recuerda este pasaje de la Ciberíada de Stanislaw Lem?

Todo el mundo sabe que los dragones no existen. Pero aunque esta formulación simplista pueda satisfacer al profano, no basta para la mente científica. De hecho, la Escuela de la Nulidad Neántica Superior se despreocupa por completo de lo que existe. De hecho, la banalidad de la existencia ha quedado tan ampliamente demostrada que no es necesario que sigamos hablando de ella aquí. El brillante Cerebrón, atacando el problema analíticamente, descubrió tres tipos distintos de dragón: el mítico, el quimérico y el puramente hipotético. Se podría decir que todos ellos eran inexistentes, pero cada uno de ellos lo era de una forma totalmente distinta.

Answer 2

La imposibilidad de este perpetuum mobile es (creo) consecuencia de que el flujo de fases preserva el volumen $dx\ dy\ d\theta$ AL MENOS SI EL PROBLEMA SE FORMULA MATEMÁTICAMENTE en términos de billar clásico (puedo imaginar formulaciones diferentes). He aquí una posible formulación matemática de los enunciados físicos, evitando la necesidad de hablar de la temperatura. Pido disculpas a los expertos por algo de lo que sigue. Afirmo que el volumen de fase del billar es una interpretación razonable de la energía del conjunto correspondiente de "fotones". Más concretamente, nuestros fotones pueden considerarse partículas que se mueven con velocidad unitaria y sufren colisiones elásticas con obstáculos. El espacio de fase es tridimensional con coordenadas $x,y,\theta$ donde $\theta$ es el ángulo de la velocidad con una dirección fija en el plano. Para justificar la afirmación anterior, partamos de un número enorme de "fotones" equidistribuidos en el espacio de fase: la densidad es casi constante. Por conservación del volumen, la densidad permanecerá constante durante todo el tiempo. Así pues, el volumen cuenta realmente el número de fotones y, por tanto, la energía, ya que cada "fotón" lleva una unidad de energía.

Ahora es fácil ver que la energía combinada de los "fotones" que chocan contra un obstáculo $c$ (por ejemplo, un disco) es igual a la energía combinada de las que rebotan (durante el mismo intervalo de tiempo). Efectivamente, $c$ es la proyección sobre $xy$ -plano del cilindro $c\times S^1$ en el espacio de fases. En la mitad de la superficie de este cilindro entra el fluido; en la otra mitad, sale. Por conservación del volumen, el flujo de entrada es igual al flujo de salida. Es decir, en el obstáculo entran tantos fotones como rebotan. Por tanto, la temperatura del obstáculo no cambia.

Answer 3

Para responder a sus dos primeras preguntas, sí, es una construcción conocida (revista de educación física, 1973).

Si los espejos están hechos de materia ordinaria y los fotones tienen algún tipo de propiedades ondulatorias, entonces todo el conjunto (incluidos los espejos) se aproximará al equilibrio térmico. Si se trata de comparar una integral de salida con una integral de entrada sin consideraciones físicas, se produce un desequilibrio. Estoy un poco oxidado en esto, pero me han dicho que la termodinámica como teoría no puede derivarse de principios físicos sin alguna aportación de la mecánica cuántica. En particular, las nociones convencionales de entropía parecen requerir algún tipo de finitud para los microestados.

Edita: Esta página trata un problema muy similar (pero con piezas esféricas en lugar de planas). La respuesta afirma que si tu cuerpo tiene un tamaño pequeño no nulo, pero espejos y fotones idealizados no físicos, sigues obteniendo una violación de la segunda ley (en contra de lo que sugieres). Más edición: La frase anterior se debe a un error de lectura: como explican los comentarios de Yuri Bajtin, un tamaño distinto de cero produce un gas fotónico homogéneo. Imagino que te refieres a la homogeneidad con la referencia a la medida de Liouville.

Answer 4

Supongo que, en el equilibrio, una parte de la energía se dispersará a lo largo de los rayos.

UPD. Como veo, esto coincide con la respuesta de Scott.

Answer 5

Hay un gran post relacionado con esto en blogs de ciencia. Defina la "radiancia" de una fuente de iluminación como la cantidad de luz que llega desde ella al observador por unidad de arco sólido. En cualquier sistema óptico pasivo, la radiancia se conserva. Cuando se utiliza un espejo curvo, por ejemplo, para enfocar los rayos del sol sobre un observador, o un objeto sólido para dar sombra parcial a un observador, lo que éste ve es que el sol parece ocupar más o menos parte del cielo: la temperatura superficial del sol parece la misma.

El problema con la configuración del espejo es que estás proponiendo fuentes de luz que son fuentes puntuales - estás tratando de dividir por cero, para tener una fuente de luz con radiancia infinita. En el momento en que haces esto, todas las apuestas se cancelan.

Para cualquier fuente de luz no puntual, la disposición no funcionará. Desde el punto de vista de muchos de los puntos de la superficie de la fuente de luz azul, la fuente de luz roja no ocupará la totalidad de su campo de visión: la imagen de la fuente roja en la elipse mayor es demasiado pequeña para ocultar por completo la imagen de la fuente azul situada detrás.