Interpretando gráficos de análisis de correspondencia 2D

Question

He estado buscando en Internet de arriba abajo... aún no he encontrado una buena descripción general sobre cómo interpretar los gráficos de análisis de correspondencias en 2D. ¿Podría alguien ofrecer algún consejo sobre cómo interpretar las distancias entre los puntos?

Tal vez un ejemplo ayudaría, aquí hay un gráfico que se encuentra en muchos de los sitios web que he visto que discuten el análisis de correspondencias. Los triángulos rojos representan el color de ojos y los puntos negros representan el color de cabello.

Observando el gráfico anterior, ¿podrías hacer algunas afirmaciones sobre lo que ves en estos datos? ¿Puntos de interés sobre las diferentes dimensiones y relaciones entre los triángulos y los puntos?

Una explicación sobre los puntos de fila versus los puntos de columna, y el uso de la palabra "perfil" con un enfoque particular en el ejemplo sería instrumental.

Answer 1

En primer lugar, existen diferentes formas de construir los llamados biplote en el caso del análisis de correspondencia. En todos los casos, la idea básica es encontrar una forma de mostrar la mejor aproximación en 2D de las "distancias" entre las celdas de filas y las celdas de columnas. En otras palabras, buscamos una jerarquía (también hablamos de "ordenación") de las relaciones entre filas y columnas de una tabla de contingencia.

Muy brevemente, el AC descompone la estadística chi-cuadrado asociada con la tabla de dos vías en factores ortogonales que maximizan la separación entre las puntuaciones de filas y columnas (es decir, las frecuencias calculadas a partir de la tabla de perfiles). Aquí, se puede ver que hay cierta conexión con el ACP pero la medida de varianza (o la métrica) retenida en el AC es el $\chi^2$, que solo depende de los perfiles de columnas (Dado que tiende a dar más importancia a las modalidades que tienen valores marginales grandes, también podemos volver a ponderar los datos iniciales, pero esa es otra historia).

Aquí tienes una respuesta más detallada. La implementación que se propone en la función corresp() (en MASS) sigue una visión del AC como una descomposición SVD de matrices codificadas en dummy que representan las filas y columnas (de modo que $R^tC=N$, con $N$ el tamaño total de la muestra). Esto concuerda con el análisis de correlación canónica. Por el contrario, la escuela francesa de análisis de datos considera el AC como una variante del ACP, donde se buscan las direcciones que maximizan la "inercia" en la nube de datos. Esto se hace mediante la diagonalización de la matriz de inercia calculada a partir de la tabla bidireccional centrada y escalada (por frecuencias marginales), y expresando los perfiles de filas y columnas en este nuevo sistema de coordenadas.

Si consideras una tabla con $i=1,\dots,I$ filas, y $j=1,\dots,J$ columnas, cada fila se pondera por su suma marginal correspondiente, lo que da una serie de frecuencias condicionales asociadas a cada fila: $f_{j|i}=n_{ij}/n_{i\cdot}$. La columna marginal se llama perfil medio (para filas). Esto nos da un vector de coordenadas, también llamado un perfil (por fila). Para la columna, tenemos $f_{i|j}=n_{ij}/n_{\cdot j}$. En ambos casos, consideraremos los $I$ perfiles de filas (asociados a su peso $f_{i\cdot}$) como individuos en el espacio de columnas, y los $J$ perfiles de columnas (asociados a su peso $f_{\cdot j}$) como individuos en el espacio de filas. La métrica utilizada para calcular la proximidad entre cualquier par de individuos es la distancia $\chi^2$. Por ejemplo, entre dos filas $i$ e $i'$, tenemos

$$ d^2_{\chi^2}(i,i')=\sum_{j=1}^J\frac{n}{n_{\cdot j}}\left(\frac{n_{ij}}{n_{i\cdot}}-\frac{n_{i'j}}{n_{i'\cdot}} \right)^2 $$

También puedes ver el vínculo con la estadística $\chi^2$ al notar que es simplemente la distancia entre las cuentas observadas y esperadas, donde las cuentas esperadas (bajo $H_0$, independencia de las dos variables) se calculan como $n_{i\cdot}\times n_{\cdot j}/n$ para cada celda $(i,j)$. Si las dos variables fueran independientes, los perfiles de filas serían todos iguales, e idénticos al perfil marginal correspondiente. En otras palabras, cuando hay independencia, tu tabla de contingencia está completamente determinada por sus márgenes.

Si realizas un ACP en los perfiles de filas (vistos como individuos), reemplazando la distancia euclidiana por la distancia $\chi^2$, entonces obtienes tu AC. El primer eje principal es la línea que está más cerca de todos los puntos, y el valor propio correspondiente es la inercia explicada por esta dimensión. Puedes hacer lo mismo con los perfiles de columnas. Se puede demostrar que hay una simetría entre los dos enfoques, y más específicamente que los componentes principales (CP) para los perfiles de columnas están asociados a los mismos valores propios que los CP para los perfiles de filas. Lo que se muestra en un biplot son las coordenadas de los individuos en este nuevo sistema de coordenadas, aunque los individuos se representan en un espacio factorial separado. Si cada individuo/modalidad está bien representado en su espacio factorial (puedes observar el $\cos^2$ de la modalidad con el 1er eje principal, que es una medida de la correlación/asociación), incluso puedes interpretar la proximidad entre elementos $i$ y $j$ de tu tabla de contingencia (como se puede hacer observando los residuos de tu prueba de independencia de $\chi^2$, por ej. chisq.test(tab)$expected-chisq.test(tab)$observed).

La inercia total de tu AC (= la suma de los valores propios) es la estadística $\chi^2$ dividida por $n$ (que es el $\phi^2$ de Pearson).

De hecho, existen varios paquetes que pueden proporcionarte CAs mejorados en comparación con la función disponible en el paquete MASS: ade4, FactoMineR, anacor y ca.

El último es el que se utilizó para tu ilustración específica, y se publicó un artículo en la Revista de Software Estadístico que explica la mayoría de sus funcionalidades: Análisis de correspondencia en R, con gráficos bidimensionales y tridimensionales: El paquete ca.

Entonces, tu ejemplo sobre colores de ojos/cabello se puede reproducir de muchas formas:

data(HairEyeColor)
tab <- apply(HairEyeColor, c(1, 2), sum) # agregado por género
tab

library(MASS)
plot(corresp(tab, nf=2))
corresp(tab, nf=2)

library(ca)
plot(ca(tab))
summary(ca(tab, nd=2))

library(FactoMineR)
CA(tab)
CA(tab, graph=FALSE)$eig  # == summary(ca(tab))$scree[,"values"]
CA(tab, graph=FALSE)$row$contrib

library(ade4)
scatter(dudi.coa(tab, scannf=FALSE, nf=2))

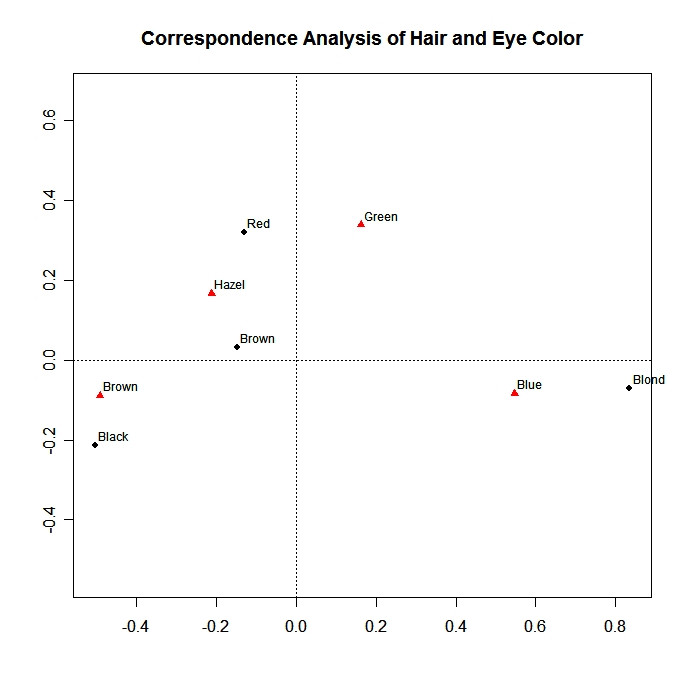
En todos los casos, lo que leemos en el biplot resultante es básicamente (limito mi interpretación al 1er eje que explicó la mayor parte de la inercia):

• el primer eje destaca la clara oposición entre el color claro y oscuro del cabello, y entre los ojos azules y marrones;
• las personas con cabello rubio tienden a tener también ojos azules, y las personas con cabello negro tienden a tener ojos marrones.

Existen muchos recursos adicionales sobre el análisis de datos en el laboratorio de bioinformática de Lyon, en Francia. La mayoría está en francés, pero creo que no debería ser un problema para ti. Los siguientes dos guiones deberían ser interesantes como primer paso:

• Iniciación al análisis factorial de las correspondencias
• Práctica del análisis de correspondencias

Finalmente, cuando consideras una codificación disyuntiva (dummy) completa de $k$ variables, obtienes el análisis de correspondencia múltiple.