Interpretación del área bajo la gráfica velocidad-tiempo de una pelota que rebota

Question

A continuación se muestra una gráfica típica de velocidad-tiempo para una pelota que rebota. Entiendo que la pelota parte del reposo a $t=0$ entonces acelera hacia abajo y golpea el suelo en el tiempo $t_1$ . Entre tiempo $t_1$ y $t_2$ El balón experimenta una reacción ascendente desde el suelo y su velocidad cambia. En el momento $t_2$ El balón abandona el suelo y rebota.

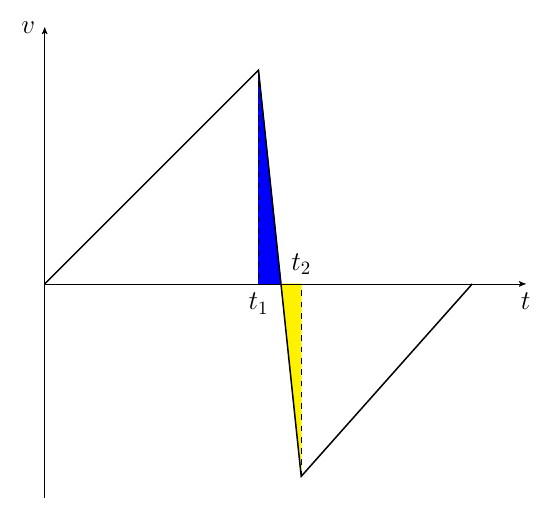
Esto es lo que me confunde. Como el área delimitada por el gráfico velocidad-tiempo puede interpretarse como la distancia recorrida. No entiendo muy bien cuál es la interpretación del trozo sombreado en azul y amarillo en el gráfico siguiente. Para una pelota que golpea el suelo a una velocidad de unos 10 metros por segundo, con un tiempo de impacto de unos 0,1 segundos, el cálculo muestra que esta distancia podría ser de hasta 0,5 metros, mucho mayor que el tamaño de una pelota de tenis. Si el tiempo de impacto es aún mayor, esta distancia también aumentaría en proporción. Pero, obviamente, durante este tiempo, la pelota no va a ninguna parte, sino que golpea con fuerza contra el suelo.

Supongo que la solución reside en el hecho de que la bola ya no puede ser tratada como una masa puntual durante el momento del impacto, ya que las velocidades en diferentes posiciones dentro de la bola serían todas diferentes. Pero sigo sin tener ni idea de lo que representan estas dos zonas coloreadas. ¿Es errónea la interpretación de la distancia? ¿O debería entenderse este gráfico de otra manera?

Answer 1

No, todo tu razonamiento es totalmente correcto. La conclusión no es que los gráficos estén equivocados, es que el tiempo de impacto es inferior a 0,1 segundos. En este vídeo Por ejemplo, el tiempo de impacto es de apenas 0,01 segundos.

Answer 2

Sí, tu razonamiento es totalmente correcto, pero es importante añadir algo de información.

El diagrama que muestras no tiene información sobre el tamaño de la bola y asume que toda la masa está concentrada en el centro de masa, que para una bola esférica e isótropa debería estar en el centro geométrico.

Ahora, en el momento del impacto $t_1$ el borde de la bola empezará a tocar el suelo y la bola empezará a deformarse. Pero en el diagrama sólo se muestra la disminución continua de la velocidad del centro de gravedad. Así que esa zona caracteriza el movimiento vertical del centro de gravedad, que como dedujiste correctamente para los valores que diste, es $0.5m$ . Así que esto ya te dice que la pelota no puede ser una pelota de tenis, tiene que ser una con un diámetro mayor que esa.

Pero espere, hay más restricciones que pueden extraerse del diagrama. El hecho de que haya una línea desde $t_1$ a $t_2$ significa que durante ese tiempo la fuerza fue constante (línea recta = aceleración constante). Esto sólo puede ser así si la deformación de la bola fue lo suficientemente pequeña como para que pueda considerarse un golpe elástico. Esto es cierto sólo deformaciones pequeñas comparadas con el radio de la esfera, porque deformaciones mayores, incluso en cuerpos elásticos, provocan fuerzas de reacción aún mayores, y la línea se convertiría en una curva parabólica (para $F=-kx$ ), o incluso cúbico.

Si simplemente equiparamos el desplazamiento del centro de masa a la compresión vertical de la bola, entonces si se desplaza $0.5m$ el estiramiento real del muelle es el doble de esa cantidad: $1m$ . Así que la bola se deformó $1m$ ¿¡Pero esto tiene que ser una pequeña deformación!?

Pequeño en este caso significaría que el radio vertical no debe comprimirse más de una cierta cantidad, que dependería de material a material, pero yo diría que no debe ser más de $10\%$ en general. Esto significaría que si $1m$ es $10\%$ del diámetro total, la esfera real que está describiendo allí debería tener un $10m$ ¡de diámetro!

Por otro lado, el tiempo de respuesta tendrá que ser considerablemente menor para una pelota de tenis, ¿no? Supongamos las mismas condiciones de fuerza elástica, y máximo $10\%$ deformación. La pelota de tenis es de $7cm$ diámetro, lo que significa que sólo puede haber comprimido $7mm$ y esto es el doble de la distancia recorrida por el centro de masa: $3.5mm$ . Lo que obtienes para la misma velocidad inicial que diste $t_2-t_1 = 0.7ms$ ¡!