(De la cruz anuncio mi respuesta de la Wikipedia mesa de ayuda.)
Aquí es una manera que usted puede realizar ingeniería inversa de la fórmula, aunque no tengo ni idea de cómo Hardy derivados.
Deje $C(x) = \cos(πx/2)$. Sabemos de la serie de Taylor que:$$C(x) = 1 - \frac{x^2}{\text{constant}} + \text{other terms}$$
Reescribir esto como $C(x) = 1 - \frac{x^2}{K(x)}$ donde K es determinado. También sabemos $C(1) = 0$ a partir de que $K(1)=1$. Expandir $K$ $x=1$ para obtener:
$$K(x)=1+(\text{constant})\cdot (x-1)+\text{higher terms}$$
De nuevo, la recolección de la constante y superior en términos de una sola función, escriba $K(x)=1+(x-1)L(x)$.
En este punto usted puede obtener una aproximación bastante buena para $C$ conectando en una aproximación lineal para $L$. Pero también sabemos $C(1/2)=\sqrt{2}/2$, lo que supondría (después de algunos cálculos) $L(1/2) = 1 - \sqrt{1/2}$. Así, tal vez, una mejor aproximación a $L$ sería: $$L(x)\approx 1 -\sqrt{\frac{1}{2}+m(x-\frac 1 2)}$$ (Para alguna constante m.)
Si conecta $C(2/3)=1/2$ obtener $m=-1/3$ que produce la aproximación dada, sino otros valores de $m$ podría funcionar igual de bien o mejor. Encontré $m=-.337$ da el menor error cuadrático medio en el intervalo.
Tenga en cuenta que hay puntos en la derivación donde diferentes opciones podría ser, por ejemplo, usted podría escribir $C(x) = 1 - x^2⋅K(x)$ o $K(x)=1+\frac{(x-1)}{L(x)}$. Podría ser divertido para explorar estas variaciones para ver cómo se comparan con la dada.
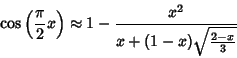 para 0<x<1
para 0<x<1

