Deseo aprender a "estimar los polos de una señal resonante", concretamente la resonancia natural compleja de los objetos.
Sin embargo, no sé qué son los "polos". ¿Qué me sugieres que busque para obtener mejores recursos? :)
Respuesta
¿Demasiados anuncios?
En primer lugar, las señales no tienen "polos", los sistemas sí.
En muchos casos, la función de transferencia de un sistema puede expresarse como una relación de dos polinomios.
$$G(s) = \frac{A_ms^m + A_{m-1}s^{m-1} + ... + A_1s + A_0}{B_ns^n + B_{n-1}s^{n-1} + ... + B_1s + B_0}$$
Existen valores de \$s\$ para el que el polinomio superior se evalúa a cero. Cuando esto ocurre, el valor de \$G(s)\$ debe ser cero, independientemente del valor del polinomio inferior. Estos valores de \$s\$ - las raíces de ese polinomio- se denominan "ceros" de la función de transferencia.
Del mismo modo, existen valores de \$s\$ para el que el polinomio inferior se evalúa a cero. Cuando esto ocurre, el valor de \$G(s)\$ va a infinito, independientemente del valor del polinomio superior. Estos valores de \$s\$ - las raíces de ese polinomio- se denominan "polos" de la función de transferencia.
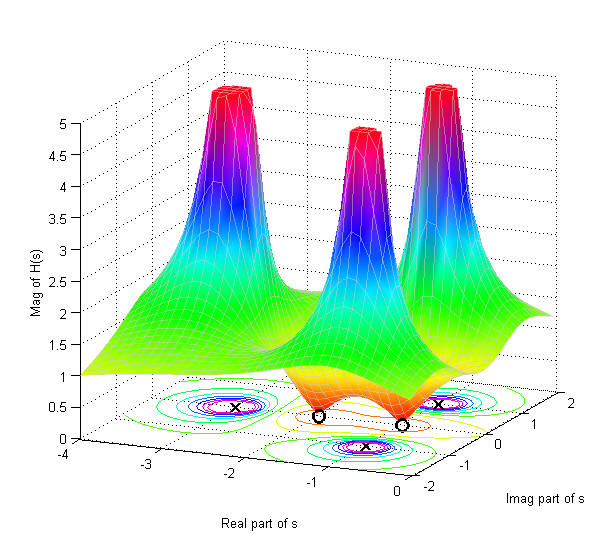
A veces imaginamos la respuesta del sistema - los valores de \$G(s)\$ - como una "lámina de goma" que se estira sobre el \$s\$ plano. Los "ceros" de la función de transferencia son los lugares donde esa hoja está pegada al \$s\$ plano, y los "polos" son frecuencias en las que la hoja es empujada hacia arriba por un polo infinitamente alto, de donde procede el término. Entre medias, la lámina encuentra valores intermedios que vienen determinados sobre todo por los polos y los ceros más cercanos.
He aquí un ejemplo de visualización:
