Tal vez te resulte aún más claro si alguien te lo explica de una manera más fundamental, pero para ello necesitamos un poco de matemáticas de nivel superior. Estoy asumiendo que has oído hablar de derivadas; si mi suposición es falsa, lo siento por eso, pero en este caso esta respuesta podría no ser útil para ti.
Vamos a aclarar algo importante (aunque más bien filosófico) primero. Esta velocidad y aceleración no son reales. Es una especie de experimento mental que resulta muy útil ya que ayuda a describir nuestro mundo.
Tomemos un objeto - sin restricción y por simplicidad, asumamos que es una manzana - y empújalo alrededor (en tu cabeza). ¿Qué está sucediendo? La posición del objeto cambia con el tiempo, por lo que aquí tenemos una conexión de dos unidades físicas fundamentales, distancia y tiempo. Puedes hablar de la distancia como una función en el tiempo (eso significa que puedes trazarla con el eje x siendo el eje del tiempo y la distancia en un tiempo dado son los valores de y).
Ahora, echemos un vistazo a la velocidad (y ahora, nuevamente por simplicidad, asumamos que el objeto viaja en línea recta, de lo contrario obtendrás espacios vectoriales más generales que pueden ser difíciles de imaginar). ¿Cómo calculas la velocidad promedio? Entonces, si la manzana hubiera estado viajando a la misma velocidad todo el tiempo, ¿qué tan grande debería ser esta velocidad?
Básicamente, la fórmula es $v_{promedio} = \frac{\text{distancia}}{\text{tiempo}}$ (bastante intuitivo, creo). Pero nuevamente, esto ya es de naturaleza teórica. No es una especie de "propiedad inherente", sino que los físicos lo han "inventado" para describir procesos.
Si no quieres calcular la velocidad promedio para toda la distancia, sino solo para un cierto período de tiempo, la fórmula sigue siendo $v_{promedio} = \frac{\text{distancia}}{\text{tiempo}}$, pero por supuesto, debes cambiar los valores de tiempo y distancia en consecuencia.
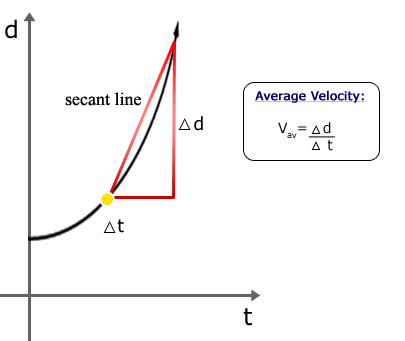
Aquí tienes una imagen:
![Velocidad promedio]()
$\Delta$ es la letra griega Delta y significa "diferencia" - diferencia entre la distancia de inicio y final y el tiempo de inicio y final. La línea recta en la imagen se llama una secante y su pendiente es igual a la distancia promedio. (Créeme en este - no sé cómo hacer que parezca más plausible en este momento.)
Ahora puedes hacerte la pregunta sobre la velocidad en un momento dado y debes darte cuenta de que la ecuación anterior ya no funcionará. Al mirar solo un punto, la diferencia entre el tiempo de inicio y final y la posición de inicio y final es cero. Ahora, no se te permite dividir por cero, y eso es un problema.
Imagina esto geométricamente: mueves uno de los dos puntos a lo largo de la curva hasta que los dos puntos son idénticos. La secante de arriba siempre ha dependido de dos puntos. Ahora, solo hay uno, por lo que teóricamente, hay una cantidad infinita de líneas que pasan por este único punto. Sin embargo, solo una línea (bueno, suponiendo que todo esto sea diferenciable - ignora eso) en realidad nos da lo que queremos. Debería ser la tangente a la curva. Ahora, eso es lo que llamamos velocidad. Todas las pendientes de las tangentes en un punto de la curva forman un nuevo gráfico que te da velocidad en función del tiempo, que es la derivada de la posición respecto al tiempo.
De manera completamente análoga, si algo está viajando, es posible que desees saber cómo cambió la velocidad. Por ejemplo, imagina un plano inclinado con nuestra manzana en él. Dependiendo del material del plano y la pendiente del mismo, la manzana puede moverse más rápido (poca fricción), mantenerse constante (fricción igual a la gravedad que empuja la manzana hacia abajo) o volverse más lenta (mucha fricción).
![ingresar descripción de la imagen aquí]()
Esto se describe con la aceleración. Si la velocidad es constante, la aceleración es cero, porque nada sucede. Si el objeto se acelera, la aceleración es positiva, porque la aceleración es la tasa de cambio de la velocidad. De manera similar, si la manzana se vuelve más lenta, hay una aceleración negativa. Ahora, para medir la aceleración promedio, hacemos lo mismo que arriba: $\text{tiempo} * \text{aceleración} = \text{velocidad} \implies \text{aceleración} = \frac{\text{velocidad}}{\text{tiempo}}$. Ahora solo mira las unidades: En el lado derecho, ya tienes metros por segundo para la velocidad, y ahora estás observando el cambio de esta velocidad con el tiempo. esto te da (metros por segundo) por segundo.
Por cierto, puedes aplicar exactamente las mismas ideas que mencioné antes (secante, tangente, derivada) al gráfico de velocidad y verás que la aceleración es la derivada de la velocidad.
Por cierto, realmente te animaría a seguir leyendo y pensando en física, matemáticas y las demás ciencias. Siempre es bueno trabajar interdisciplinariamente y creo que es crucial para un filósofo saber lo que esas personas de ciencias parecen "saber" sobre todo lo que hay ahí fuera. He visto a demasiados filósofos construir teorías que simplemente - bueno - no coincidían con la realidad.
Creo que, esta serie de YouTube sobre el tema está muy bien hecha y puede que disfrutes viéndola.