¿Cuál es la diferencia entre redes neuronales convolucionales y aprendizaje profundo?

Question

Quiero usar el aprendizaje profundo en mi proyecto. Revisé un par de papers y me surgió una pregunta: ¿hay alguna diferencia entre la red neuronal convolucional y el aprendizaje profundo? ¿Son las mismas cosas o tienen alguna diferencia importante, y cuál es mejor?

Answer 1

El Aprendizaje Profundo es la rama del Aprendizaje Automático basada en Redes Neuronales Profundas (DNNs), lo que significa redes neuronales con al menos 3 o 4 capas (incluyendo las capas de entrada y salida). Sin embargo, para algunas personas (especialmente no técnicas), cualquier red neuronal califica como Aprendizaje Profundo, independientemente de su profundidad. Y otros consideran que una red neuronal de 10 capas es superficial.

Las Redes Neuronales Convolucionales (CNNs) son una de las arquitecturas de redes neuronales más populares. Son extremadamente exitosas en el procesamiento de imágenes, pero también para muchas otras tareas (como el reconocimiento de voz, el procesamiento del lenguaje natural, entre otros). Las CNNs de vanguardia son bastante profundas (decenas de capas al menos), por lo que forman parte del Aprendizaje Profundo. Pero se puede construir una CNN superficial para una tarea simple, en cuyo caso no es (realmente) Aprendizaje Profundo.

Pero las CNNs no están solas, existen muchas otras arquitecturas de redes neuronales, incluyendo Redes Neuronales Recurrentes (RNN), Autoencoders, Transformers, Deep Belief Nets (DBN = una pila de Máquinas de Boltzmann Restringidas, RBM), y más. Pueden ser superficiales o profundas. Nota: incluso las RNNs superficiales pueden considerarse parte del Aprendizaje Profundo ya que entrenarlas requiere desplegarlas en el tiempo, lo que resulta en una red profunda.

Answer 2

Dentro de los campos del procesamiento de señales adaptativo/aprendizaje automático, deep learning (DL) es una metodología particular en la cual podemos entrenar a las máquinas para que generen representaciones complejas.

Generalmente, tendrán una formulación que puede mapear su entrada $\mathbf{x}$, hasta el objetivo deseado, $\mathbf{y}$, a través de una serie de operaciones apiladas jerárquicamente (aquí es de donde proviene lo 'profundo'). Estas operaciones suelen ser operaciones/proyecciones lineales ($W_i$), seguidas de no linealidades ($f_i$), de la siguiente manera:

$$ \mathbf{y} = f_N(...f_2(f_1(\mathbf{x}^T\mathbf{W}_1)\mathbf{W}_2)...\mathbf{W}_N) $$

Ahora dentro del DL, hay muchas arquitecturas diferentes: Una de esas arquitecturas es conocida como una red neuronal convolucional (CNN). Otra arquitectura es conocida como un perceptrón multicapa (MLP), etc. Diferentes arquitecturas se prestan para solucionar diferentes tipos de problemas.

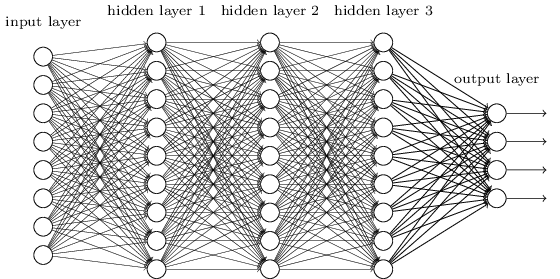
Un MLP es quizás uno de los tipos de arquitecturas de DL más tradicionales que se pueden encontrar, y en este caso cada elemento de una capa previa está conectado con cada elemento de la capa siguiente. Se ve así:

En los MLPs, las matrices $\mathbf{W}_i$ codifican la transformación de una capa a otra. (A través de una multiplicación de matrices). Por ejemplo, si tienes 10 neuronas en una capa conectadas a 20 neuronas en la siguiente, entonces tendrás una matriz $\mathbf{W} \in R^{10 \text{x} 20}$, que mapeará una entrada $\mathbf{v} \in R^{10 \text{x} 1}$ a una salida $\mathbf{u} \in R^{1 \text{x} 20}$, a través de: $\mathbf{u} = \mathbf{v}^T \mathbf{W}$. Cada columna en $\mathbf{W}$ codifica todas las conexiones desde todos los elementos de una capa, hacia uno de los elementos de la siguiente capa.

Los MLPs cayeron en desuso entonces, en parte porque eran difíciles de entrenar. Aunque hay muchas razones para esa dificultad, una de ellas también fue que sus conexiones densas no les permitían escalar fácilmente para varios problemas de visión por computadora. En otras palabras, no tenían incorporada la equivarianza a la traslación. Esto significa que si había una señal en una parte de la imagen a la que necesitaban ser sensibles, deberían aprender nuevamente a ser sensibles a ella si esa señal se movía. Esto desperdiciaba la capacidad de la red y hacía que el entrenamiento fuera difícil.

¡Aquí es donde entran las CNNs! Así es como se ven:

Las CNNs resolvieron el problema de traslación de señal, porque convolucionaban cada señal de entrada con un detector (núcleo) y así eran sensibles a la misma característica, pero esta vez en todas partes. En ese caso, nuestra ecuación sigue viéndose igual, pero las matrices de pesos $\mathbf{W_i}$ son en realidad matrices toeplitz convolucionales. Aunque las matemáticas son las mismas.

Es común ver que "CNNs" se refieran a redes donde tenemos capas convolucionales a lo largo de toda la red, y MLPs al final, por lo que este es un detalle a tener en cuenta.

Answer 3

Deep learning = redes neuronales artificiales profundas + otro tipo de modelos profundos.

Redes neuronales artificiales profundas = redes neuronales artificiales con más de 1 capa. (ver número mínimo de capas en una red neuronal profunda o Wikipedia para más debate…)

Redes Neuronales Convolucionales = Un tipo de redes neuronales artificiales

Answer 4

Esta diapositiva de Yann LeCun señala que solo los modelos con una jerarquía de características (las características de nivel inferior se aprenden en una capa de un modelo y luego esas características se combinan en el siguiente nivel) son profundos.

Una CNN puede ser profunda o superficial; en el caso de que siga esta construcción de "jerarquía de características" porque ciertas redes neuronales, incluidos los modelos de 2 capas, no son profundas.

Answer 5

Aprendizaje profundo es un término general para lidiar con una red neuronal complicada con múltiples capas. No hay una definición estándar de lo que exactamente es profundo. Por lo general, se puede pensar que una red profunda es algo demasiado grande para que tu portátil y PC lo puedan entrenar. El conjunto de datos sería tan grande que no podrías ajustarlo en tu memoria. Es posible que necesites una GPU para acelerar tu entrenamiento.

Profundo es más como un término de marketing para hacer que algo suene más profesional de lo contrario.

CNN es un tipo de red neuronal profunda, y existen muchos otros tipos. Las CNN son populares porque tienen aplicaciones muy útiles en el reconocimiento de imágenes.