Mi entendimiento es que, a la tasa actual de expansión del universo, algunas galaxias se están alejando cada vez más de nosotros a tal velocidad que la luz de ellas nunca nos alcanzará. Mi pregunta es: ¿a qué distancia debe estar una galaxia para que esto sea cierto de ella?
Respuestas
¿Demasiados anuncios?Si nuestras ideas sobre la evolución cósmica son correctas, en principio las galaxias que son visibles hoy en día seguirán siendo visibles en el futuro. A medida que pasa el tiempo, la luz de galaxias cada vez más distantes podrá llegar hasta nosotros, y el número de galaxias observables aumentará.
Sin embargo, existe un horizonte de eventos cósmico$^1$, por lo que se trata de un crecimiento asintótico: Hay un número máximo de galaxias que un observador futuro en principio podrá detectar.
El problema es que el corrimiento al rojo hará que las galaxias en recesión parezcan cada vez más débiles, por lo que en la práctica verás menos y menos galaxias, y algún día no podrás detectar galaxias distantes en absoluto. Esto se debe a limitaciones puramente tecnológicas, no a razones fundamentales como las galaxias que abandonan la esfera de Hubble (no hay nada realmente especial sobre la distancia donde las velocidades de recesión alcanzan $c$) o cruzan el horizonte de eventos cósmico (las galaxias quedan congeladas en el tiempo mientras se acercan al horizonte en lugar de cruzarlo).
La distancia a la galaxia más lejana que será observable, por supuesto, cambia con la expansión métrica del espacio. Si sigues la respuesta de Pulsar a una pregunta relacionada, el tamaño del universo asintóticamente observable será de aproximadamente $60\mathrm{Gly}$ medido en distancia en movimiento coherente:
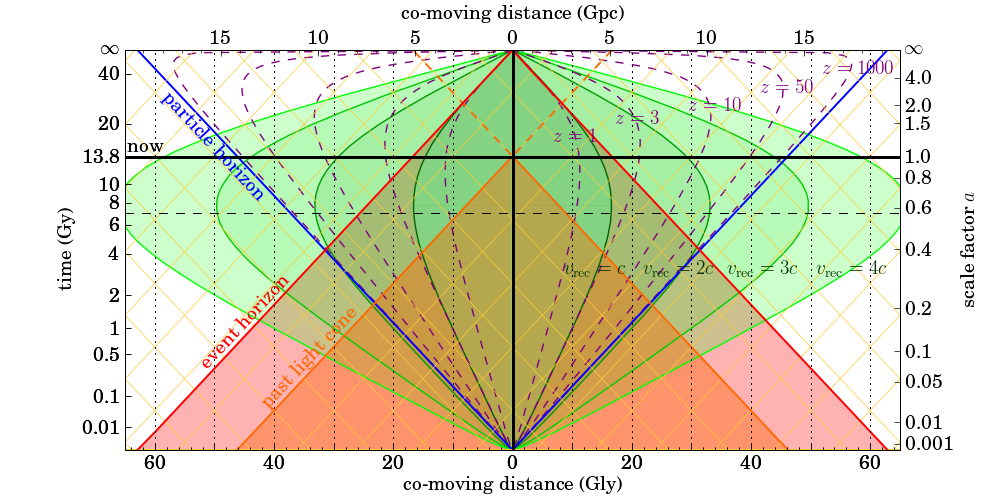
$^1$ Si existen galaxias más allá del horizonte de eventos cósmico (lo cual es plausible), la luz desde más allá del horizonte está en camino hacia nosotros, simplemente tarda un tiempo más largo que infinito en llegar. En la imagen de arriba, no hay nada especial sobre la región fuera del cono rojo.
En este documento de Gott et al., en la p. 466 ellos definen el "límite de visibilidad futura", diciendo en la versión publicada que "No importa cuánto esperemos, no podremos ver más allá de esto", y en la preimpresión de arxiv en la p. 7 ellos dicen de manera similar "Si esperamos hasta el futuro infinito eventualmente podremos ver el Big Bang en el límite de visibilidad futura co-móvil. Estrellas y galaxias que están más allá de este límite de visibilidad futura co-móvil están para siempre ocultas de nuestra vista." El texto bajo la Fig. 1 en la p. 467 del documento (p. 43 de la preimpresión de arxiv) da el límite de visibilidad futura como 4.5 veces el radio de Hubble, mencionado en la p. 465 (p. 7 de la preimpresión) como 4220 Mpc, que es equivalente a 13.76 mil millones de años luz. Por lo tanto, si el límite de visibilidad futura es 4.5 veces eso, debería ser cerca de 62 mil millones de años luz, lo cual coincide con donde el cono de "horizonte de eventos" cosmológico alcanza el eje de "distancia comóvil" en el tercer diagrama en la Fig. 1 en este documento de Davis y Lineweaver (el texto debajo dice que "Nuestro horizonte de eventos es nuestro cono de luz pasado al final del tiempo, $t = \infty$ en este caso", así que evidentemente esto es lo mismo que el límite de visibilidad futura).
Ten en cuenta que esto puede en realidad no ser exactamente lo que estás preguntando, porque el diagrama en el segundo documento indica que el horizonte de eventos del cual están hablando es la distancia comóvil tal que nunca veremos luz emitida desde esa ubicación en cualquier momento, incluso arbitrariamente cerca del Big Bang. (Si no estás familiarizado con el término, distancia comóvil está definida de manera que un par promedio de galaxias mantendrá una distancia comóvil fija, básicamente dejando fuera la expansión del espacio, y también está definida de manera que la distancia comóvil a una galaxia en el presente es idéntica a su distancia propia presente, es decir, la distancia que sería medida por una serie de pequeñas reglas colocadas una tras otra en el tiempo cosmológico presente.) Puede que en realidad estabas preguntando acerca de la distancia comóvil tal que si la luz fuera emitida desde esa ubicación ahora, nunca nos llegaría. No tengo un documento que dé un número preciso para esta distancia, pero mirando dónde el horizonte de eventos (el cono de luz pasado de nuestra ubicación en $t=\infty$) intersecciona el eje de "ahora" en el tercer diagrama en la Fig. 1 del documento de Davis/Lineweaver, junto con el diagrama prácticamente idéntico creado por Pulsar que aparece en la respuesta de Christoph, si usas un programa de dibujo para trazar una línea recta entre el punto de intersección y el eje de "distancia comóvil", parece que la respuesta está muy cerca de 16 mil millones de años luz.
Además de las respuestas ya dadas:
Hay que diferenciar entre las galaxias cuya luz que emiten hoy puede ser recibida por nosotros en el futuro, y las galaxias cuya luz que emitieron en el pasado hasta el big bang que podemos recibir hoy y en el futuro.
La primera es el horizonte de eventos cósmico (16 Glyr), que actualmente está un poco más lejos que el radio de Hubble (en unos pocos mil millones de años cuando la densidad de materia se vuelva despreciable en comparación con la energía oscura, serán iguales). Converge a una distancia propia de aproximadamente 18 Glyr, mientras su distancia co-móvil se reduce.
Eso significa que las galaxias detrás del radio de Hubble (14 Glyr), pero dentro del horizonte de eventos (16 Glyr) con una velocidad de recesión mayor que c todavía pueden enviarnos una señal que podremos recibir en el futuro. En tiempos posteriores, ambos radios convergerán a 18 Glyr.
La segunda es el horizonte de partículas (46 Glyr), ése tiene una distancia propia en crecimiento exponencial, mientras su distancia co-móvil converge a 64 Glyr.
Eso significa que los objetos cuya luz que recibimos hoy fue emitida poco después del big bang están ahora a 46 Glyr de distancia, mientras que más adelante también veremos la infancia temprana de objetos que están actualmente a 64 Glyr de distancia.
La razón por la cual la distancia propia del horizonte de eventos y la distancia co-móvil del horizonte de partículas convergen a un valor fijo en el futuro es porque el parámetro de Hubble también está convergiendo a un valor constante debido a la expansión acelerada (constante cosmológica), que será alrededor de H0√Ωλ, que es aproximadamente el 83% de la tasa de expansión actual (ver también aquí).
Eso se puede ver en el diagrama de distancia propia versus distancia co-móvil, para una comparación ver aquí (se parece mucho a la imagen en la otra respuesta, pero el eje de tiempo es lineal, mientras que en la imagen mostrada en la respuesta de Christoph las curvas se aplanan usando un eje de tiempo conforme).
He argumentado que el Universo está rotando en lugar de expandirse al conectar la velocidad y aceleración newtonianas con la velocidad y aceleración cósmicas respectivamente usando un algebra simple. El argumento para un Universo rotatorio en lugar de un Universo en expansión es el siguiente:
$$v = \sqrt{\frac{G M}{r}} = \frac{r}{r} \sqrt{\frac{G M}{r}} = r \sqrt{\frac{G M}{r^3}} = r H$$
$$a = \frac{G M}{r^2} = \frac{r}{r} \frac{G M}{r^2} = r \frac{G M}{r^3} = r H^2 = v H$$
$$H^2 = \frac{G M}{r^3} = (G \cdot \text{densidad de masa}) = t^{-2}$$
donde $v$ es la velocidad newtoniana, $a$ es la aceleración newtoniana, $v = r H$ es la ley de Hubble o la velocidad cósmica, $a = r H^2 = v H$ es la aceleración cósmica que afecta a la luz y a las sondas Pioneer, y así sucesivamente.
Esto significa que el Universo está rotando en lugar de expandirse, y por lo tanto no hay lugar para la expansión dentro de las leyes de la gravedad. En este escenario, el corrimiento al rojo cósmico se debe a la dilatación del tiempo de la luz en lugar de la separación de galaxias entre sí. La expansión de la que habla el Sagrado Corán es la que ocurrió durante la formación del Universo y que se detuvo temprano en la historia cósmica, dejando paso a la gravedad.
La segunda cosa es que se ha encontrado que la velocidad de la luz significa la velocidad de escape de la luz en la posición de la Tierra en el campo gravitacional cósmico al igualar la energía de la luz a la energía potencial gravitacional cósmica. El argumento para la equivalencia entre la velocidad de la luz y la velocidad de escape de la luz en el campo gravitacional cósmico es el siguiente:
$$E = m c^2 = \frac{G M m}{r}$$
lo que da $$c = \sqrt{\frac{G M}{r}}$$
Consecuentemente, podemos usar la ecuación $c = r H$ para calcular la distancia desde el centro del Universo hasta la posición de la Tierra en el Universo, que se calcula que es alrededor de $1.28 \cdot 10^{26}$ metros o $13.80$ mil millones de años luz. Esta distancia no tiene nada que ver con el radio del Universo medido ni con el Universo observable como generalmente se cree.
El tercer punto es que la distancia de grosor del Universo se obtiene mirando hacia atrás en el tiempo al instante del Big Bang y es de alrededor de $63$ mil millones de años luz utilizando la técnica de distancia comóvil en cosmología teórica.
Por lo tanto, la distancia que separa la Tierra del límite del Universo se puede calcular restando la distancia entre el centro del Universo y la Tierra que es igual a $1.28 \cdot 10^{26}$ metros o $13.80$ mil millones de años luz de la distancia de grosor del Universo que es igual a $5.78 \cdot 10^{26}$ metros o $63$ mil millones de años luz.
Siguiendo este enfoque, se encuentra que la distancia que separa la Tierra del límite del Universo es de alrededor de $4.50 \cdot 10^{26}$ metros o $50$ mil millones de años luz, es decir, $r' = (5.78 - 1.28) \cdot 10^{26}$ metros = $4.5 \cdot 10^{26}$ metros o $r' = (63 - 13.80)$ mil millones de años luz = $49.20$ mil millones de años luz.


