Tres versiones del análisis discriminante: diferencias y cómo utilizarlas

Question

¿Puede alguien explicar las diferencias y dar ejemplos concretos de cómo utilizar estos tres análisis?

• LDA - Análisis discriminante lineal
• FDA - Análisis discriminante de Fisher
• QDA - Análisis discriminante cuadrático

He buscado por todas partes, pero no he podido encontrar ejemplos reales con valores reales para ver cómo se utilizan estos análisis y se calculan los datos, sólo un montón de fórmulas que son difíciles de entender sin ningún ejemplo real. Mientras intentaba entender era difícil distinguir qué ecuaciones/fórmulas pertenecían a LDA y cuáles a FDA.

Supongamos, por ejemplo, que existen estos datos:

x1 x2 class
1  2  a
1  3  a
2  3  a
3  3  a
1  0  b
2  1  b
2  2  b

Y digamos que algunos datos de las pruebas:

x1 x2
2  4
3  5
3  6

Entonces, ¿cómo utilizar estos datos con estos tres enfoques? Lo mejor sería ver cómo calcular todo a mano, y no utilizar algún paquete matemático que lo calcule todo entre bastidores.

P.D. Sólo he encontrado este tutorial: http://people.revoledu.com/kardi/tutorial/LDA/LDA.html#LDA . Muestra cómo utilizar el LDA.

Answer 1

"El análisis discriminante de Fisher" es simplemente LDA en una situación de 2 clases. Cuando sólo hay 2 clases los cálculos a mano son factibles y el análisis está directamente relacionado con la Regresión Múltiple. El LDA es la extensión directa de la idea de Fisher en situaciones de cualquier número de clases y utiliza dispositivos de álgebra matricial (como la eigendecomposición) para calcularlo. Por lo tanto, el término "Análisis Discriminante de Fisher" puede considerarse obsoleto en la actualidad. En su lugar, debería utilizarse "Análisis discriminante lineal". Ver también . El análisis discriminante con 2+ clases (multiclase) es canónico por su algoritmo (extrae dicriminantes como variantes canónicas); el raro término "Análisis Discriminante Canónico" suele significar simplemente LDA (multiclase) por tanto (o LDA + QDA, omnicanal).

Fisher utilizó lo que entonces se denominó "funciones de clasificación de Fisher" para clasificar los objetos una vez calculada la función discriminante. En la actualidad, se utiliza un enfoque de Bayes más general dentro del procedimiento LDA para clasificar los objetos.

A su solicitud de explicaciones sobre la LDA puedo enviarle a estas mis respuestas: extracción en LDA , clasificación en LDA , LDA entre los procedimientos relacionados . También este , este , este preguntas y respuestas.

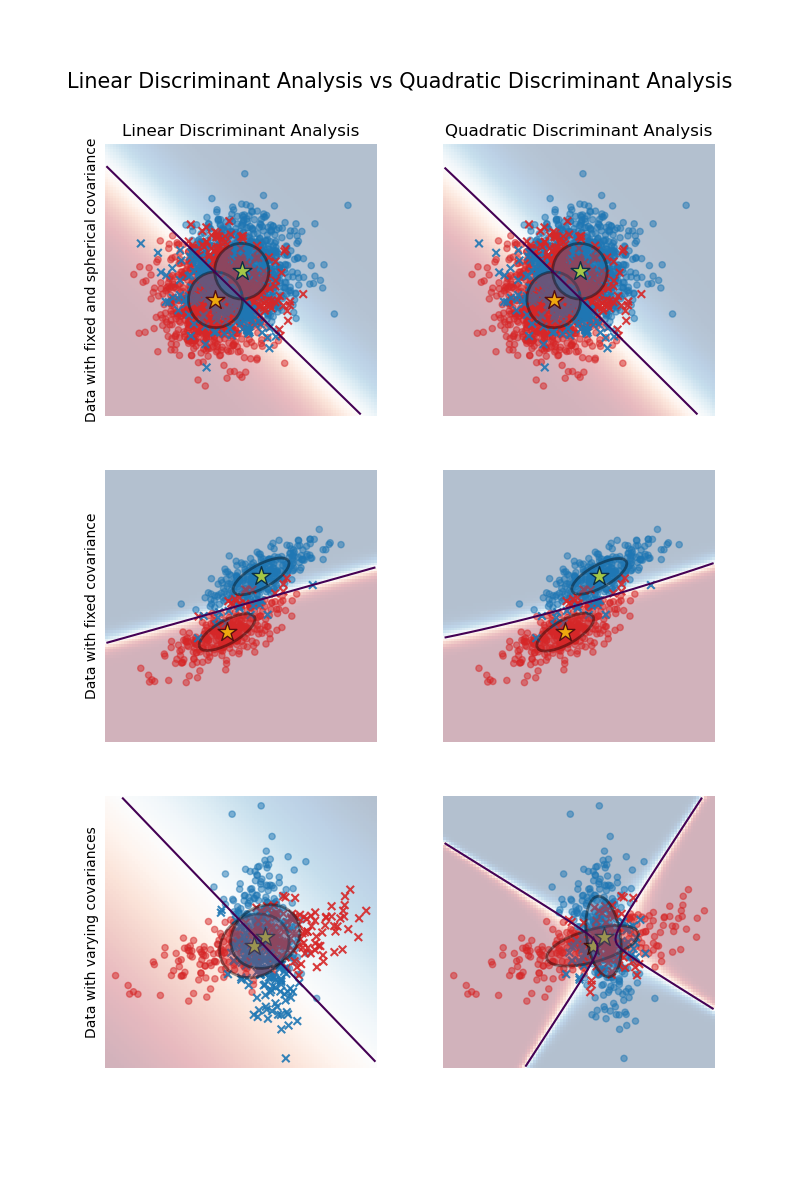
Al igual que el ANOVA requiere una suposición de varianzas iguales, el LDA requiere una suposición de matrices de varianza-covarianza iguales (entre las variables de entrada) de las clases. Esta suposición es importante para la fase de clasificación del análisis. Si las matrices difieren sustancialmente, las observaciones tenderán a asignarse a la clase en la que la variabilidad sea mayor. Para superar el problema, QDA se inventó. El QDA es una modificación del LDA que permite la mencionada heterogeneidad de las matrices de covarianza de las clases.

Si se tiene la heterogeneidad (detectada, por ejemplo, por la prueba M de Box) y no se tiene el QDA a mano, aún se puede utilizar el LDA en el régimen de uso de las matrices de covarianza individuales (en lugar de la matriz agrupada) del discriminantes en la clasificación. Esto resuelve en parte el problema, aunque con menos eficacia que en QDA, porque -como se acaba de señalar- se trata de las matrices entre los discriminantes y no entre las variables originales (cuyas matrices difieren).

Permíteme que deje el análisis de los datos de tu ejemplo para ti.

---

Responder a Respuesta de @zyxue y comentarios

LDA es lo que usted definió como FDA en su respuesta. LDA primero extrae constructos lineales (llamados discriminantes) que maximizan la separación entre y dentro, y entonces los utiliza para realizar una clasificación (gaussiana). Si (como dices) el LDA no estuviera ligado a la tarea de extraer los discriminantes el LDA parecería ser sólo un clasificador gaussiano, no sería necesario el nombre "LDA" en absoluto.

Es que clasificación etapa en la que el LDA asume tanto normalidad y homogeneidad de varianza-covarianza de las clases. El extracción o etapa de "reducción de la dimensionalidad" del LDA supone linealidad y homogeneidad de varianza-covarianza Las dos suposiciones juntas hacen que la "separabilidad lineal" sea factible. (Usamos un único grupo de $S_w$ para producir discriminantes que, por lo tanto, tienen una matriz de covarianza conjunta dentro de la clase, que nos da derecho a aplicar el mismo conjunto de discriminantes para clasificar a todas las clases. Si todos los $S_w$ s son iguales las citadas covarianzas dentro de la clase son todas iguales, identidad; ese derecho a utilizarlas se convierte en absoluto).

El clasificador gaussiano (la segunda etapa de LDA) utiliza la regla de Bayes para asignar las observaciones a las clases por los discriminantes. El mismo resultado puede obtenerse mediante las llamadas funciones de clasificación lineal de Fisher, que utilizan directamente las características originales. Sin embargo, el enfoque de Bayes basado en los discriminantes es un poco más general en el sentido de que permitirá utilizar también las matrices de covarianza de los discriminantes de las clases por separado, además de la forma predeterminada de utilizar una, la agrupada. Además, permitirá basar la clasificación en un subconjunto de discriminantes.

Cuando sólo hay dos clases, las dos etapas de LDA pueden describirse juntas en una sola pasada porque la "extracción de latentes" y la "clasificación de observaciones" se reducen entonces a la misma tarea.

Answer 2

Me resulta difícil estar de acuerdo con que la FDA sea LDA para dos clases como sugirió @ttnphns.

Recomiendo dos conferencias muy informativas y hermosas sobre este tema del profesor Ali Ghodsi:

1. LDA Y QDA . Además, la página 108 del libro Los elementos del aprendizaje estadístico ( pdf ) tiene una descripción del LDA coherente con la conferencia.
2. FDA

Para mí, LDA y QDA son similares, ya que ambas son técnicas de clasificación con supuestos gaussianos. La principal diferencia entre ambas es que el LDA asume que las matrices de covarianza de las características de ambas clases son las mismas, lo que da lugar a un límite de decisión lineal. En cambio, el QDA es menos estricto y permite diferentes matrices de covarianza de características para diferentes clases, lo que da lugar a un límite de decisión cuadrático. Véase la siguiente figura de scikit-learn para hacerse una idea del aspecto de la frontera de decisión cuadrática.

Algunos comentarios sobre las subtramas :

• Fila superior: cuando las matrices de covarianza son efectivamente las mismas en los datos, LDA y QDA conducen a los mismos límites de decisión.
• Fila inferior: cuando las matrices de covarianza son diferentes, el LDA tiene un mal rendimiento, ya que su suposición no es válida, mientras que el QDA realiza la clasificación mucho mejor.

Por otro lado, la FDA es una especie muy diferente, que no tiene nada que ver con la suposición de Gaussion. Lo que la FDA trata de hacer es encontrar una transformación lineal para maximizar la distancia media entre clases y minimizar la varianza dentro de la clase . La segunda conferencia explica muy bien esta idea. En contraste con LDA/QDA, FDA no hace la clasificación, aunque las características obtenidas después de la transformación encontrada por FDA podría ser utilizado para la clasificación, por ejemplo, utilizando LDA/QDA, o SVM u otros.