¿Por qué hay tan pocas operaciones con aridad mayor que 2?

Question

En las estructuras algebraicas habituales, como los grupos, anillos, monoides, etc, o en las álgebras procedentes de la lógica como las álgebras booleanas, las álgebras de Heyting y similares las operaciones suelen ser de aridad 0 (constantes), 1 o 2. Mi pregunta es doble:

1. Proporcione ejemplos de álgebras que surjan de forma natural en algún campo (me interesan principalmente las álgebras procedentes de la lógica, pero estoy abierto a cualquier campo) con operaciones de aridad 3 o mayor.

2. ¿Hay alguna razón (más o menos profunda) para que haya tan pocas álgebras con operaciones de aridad mayor que 2?

Gracias de antemano.

Answer 1

En el análisis de Fourier de orden superior, existen estructuras d-dimensionales de tipo paralelepípedo que pueden ser vistas como un $2^d-1$ -relación de tipo "dado todos los vértices menos uno de un paralelogramo como entrada, devuelve el vértice final como salida". (En este caso, "paralelogramo" debe interpretarse en un sentido abstracto adecuado, como una familia de $2^d$ -tuplas que obedecen a un cierto número de axiomas). Este punto de vista se adopta, por ejemplo, en este trabajo de Camarena y Szegedy , basándose en el trabajo anterior de Host y Kra . En el caso d=2, esta operación ternaria es esencialmente equivalente a una operación aditiva una vez que se fija un origen (en cuyo caso la operación ternaria se convierte en $(x,y,z) \mapsto x-y+z$ ). Para d=3, estas operaciones se rigen por grupos nilpotentes de 2 pasos, y de forma más general las estructuras de paralelopípedos de d dimensiones se rigen por grupos nilpotentes de d-1 pasos.

Estas estructuras de paralelopípedos pueden verse como el fundamento abstracto de las normas de uniformidad de Gowers, y también comparten cierto parecido formal con los complejos cúbicos, que son construcciones que aparecen sobre todo en topología algebraica y que se discuten por ejemplo aquí . Existe una versión simplificada de este último concepto conocida como Complejo Kan pero no conozco los detalles de cómo se utilizan. Pero creo que los complejos Kan vienen equipados con relaciones de alta aridad de la forma general "dados los datos de todas las caras de un simplex menos una, suministrar los datos de la cara restante (y también del interior) de ese simplex". Entre otras cosas, tales estructuras pueden utilizarse para definir n-grupos; véase, por ejemplo la entrada de mi blog sobre este tema .

Answer 2

En la teoría de los nudos, empalme generalmente tiene más de una o dos entradas.

El empalme con una entrada genera cosas como los dobles de Whitehead:

y el cableado:

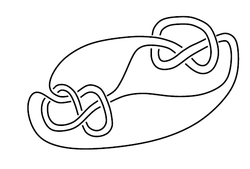
Hay muchos $n$ -Operaciones de carácter secundario. La primera que se ha observado (históricamente) es la suma de conexiones: . El problema que se puede tener con el $n$ -ary connect-sum es su generado por el 2-ary connect sum. Así que aquí tenemos un ejemplo de $2$ -empalme de la columna vertebral que no es una suma de conexión:

Hay una colección infinita contable de $n$ -ary splices para cualquier $n \geq 1$ Además, sigue habiendo un número contablemente infinito de primitivas para cualquier $n \geq 1$ donde primitivo significa "no se puede expresar en términos de $j$ -Estas operaciones primitivas de empalme resultan estar especificadas (únicamente) por la hiperbólica $(n+1)$ -enlaces de componentes en la 3-esfera $L \subset S^3$ , $L=L_0 \sqcup L_1 \sqcup \cdots \sqcup L_n$ de manera que el subenlace $L_1 \sqcup \cdots \sqcup L_n$ es el enlace trivial. La hiperbolicidad significa $S^3 \setminus L$ tiene una estructura hiperbólica completa de volumen finito.

El empalme puede situarse en un marco operádico y éste es el tema de uno de mis trabajos. Así que también se puede convertir en un formalismo puramente algebraico, tomando la homología del espacio de todos los nudos y la operada de empalme, respectivamente.

No tengo claro que haya ninguna razón por la aparente prevalencia de las operaciones 2-arias en las matemáticas. Parece ser más bien un accidente: dos cosas que interactúan es más simple, más fácil de contemplar.

Answer 3

¿Es esto como la pregunta de por qué las matrices son más comunes que las multimatrices? Siéntase libre de marcar esto como spam porque no tengo suficientes dólares de mathoverflow para comentar.

Answer 4

Alguien ya ha mencionado los determinantes. Aquí hay una relación $n$ -la operación de producto vectorial en dimensión $n+1$ : Fijar una base $b_1,\dots,b_{n+1}$ de $\mathbb R^{n+1}$ . A $n$ elementos $v_1,\dots,v_n$ de $\mathbb R^{n+1}$ asignar el vector único $v_{n+1}$ que es ortogonal a $v_1,\dots,v_n$ , de tal manera que $v_1,\dots,v_{n+1}$ tiene la misma orientación que $b_1,\dots,b_{n+1}$ y tal que el longitud de $v_{n+1}$ es el $n$ -del volumen del paralelepípedo que se extiende por $v_1,\dots,v_n$ .

Answer 5

Para añadir a la lista de ejemplos:

1. Heaps tienen una única operación ternaria (identidades en la página enlazada). En resumen, un montón es a un grupo lo que un espacio afín es a un espacio vectorial: en cuanto se elige una identidad se obtiene un grupo.

2. Espacios totalmente convexos que son espacios que permiten combinaciones convexas arbitrarias. Ejemplos sencillos son las bolas unitarias de los espacios vectoriales normados, pero otros como $(0,1)$ existe.

3. De la misma manera, $C^*$ -y hay una teoría estrechamente relacionada con las álgebras de Banach. Véase esta página en el nLab donde empecé a reunir algunos detalles sobre estos.

Para responder a la cuestión de por qué a menudo sólo utilizamos operaciones de aridad como máximo 2, he aquí un pequeño dato interesante. Abstractamente, podemos considerar operaciones de aridad arbitraria con identidades arbitrarias, pero en situaciones concretas las operaciones suelen tener un alto nivel de compatibilidad. Una de las más comunes es la conmutatividad. Se trata de la conmutatividad de las operaciones, que es ligeramente diferente de lo que normalmente consideramos como conmutatividad (aunque ambas están muy relacionadas). Si tenemos una operación binaria con una unidad, entonces cualquier operación que conmuta con esa operación (y su unidad) resulta estar formada por la iteración de la operación binaria. Se trata de una generalización sencilla de la Argumento de Eckmann-Hilton . Por lo tanto, una vez que empezamos a aplicar las identidades comunes, encontramos que a menudo podemos reducir la aridad a algo aceptable.