¿Por qué es constante la vida media radioactiva?

Question

Digamos que tienes solo cuatro átomos radiactivos con una vida media de una hora. (Estoy usando un número pequeño de átomos para mantenerlo simple e ilustrar mi confusión de manera más clara). Eso significa que una hora a partir de ahora, dos de los átomos habrán decaído (en promedio) y dos permanecerán sin decaer (en promedio). Ahora, estoy luchando por entender por qué los últimos dos átomos sin decaer no deberían, en promedio, decaer ambos en la siguiente hora. Después de todo, si tomó una hora para que los primeros dos átomos decaigan, entonces seguramente debería tomar una hora más para que dos átomos más decaigan...

En general, si toma x años para que la mitad de una muestra decaiga, ¿no debería lógicamente tomar otros x años para que toda la otra mitad de la muestra decaiga? Obviamente, este no es el caso, pero estoy luchando por entender por qué no es el caso... Es casi como si los átomos en una muestra de alguna manera 'supieran' cuántos otros átomos hay en la muestra...

Answer 1

Podría ayudarte pensar en términos de lanzar monedas o tirar dados. Digamos que lanzas un montón de monedas cada minuto y te deshaces de todas las que salen con la cara. La colección de monedas tendría una vida media de un minuto. El punto es que las monedas (átomos) no saben nada sobre cuántas hay o cuánto tiempo han estado esperando para decaer.

Answer 2

No funciona en algo como 4 átomos, o incluso cien átomos. Es estadístico, por lo que necesitas muchos muchos átomos.

Lo que estás haciendo es como calcular la derivada para encontrar la pendiente en un punto de una curva, y luego decir que no entiendes por qué la curva no tiene una pendiente constante. Has asumido erróneamente que el valor que has calculado es fundamental para el comportamiento de la cosa que estás observando.

En términos fundamentales, NO es que haya "n átomos decayendo cada minuto". Ese es tu error. Más bien, es que cada átomo específico tiene una probabilidad de decaer en cierto intervalo de tiempo.

Pero cuando tienes un bloque de material, no te importa que un átomo individual en particular haya decaído. Solo te importa que un átomo haya decaído, ya que todos los átomos son intercambiables.

Imagina la probabilidad de que una persona sea alcanzada por un rayo; es muy baja. Pero si tu población es enorme, hay casi un 100% de probabilidad de que alguna cantidad de personas, en algún lugar, serán alcanzadas por un rayo durante el próximo año. Esto resulta en una tasa en la que cierta cantidad de personas son alcanzadas por un rayo cada año.

Aunque la probabilidad de que una persona en particular sea alcanzada por un rayo permanece igual, la tasa a la que las personas son alcanzadas por un rayo depende de cuántas personas quedan. A medida que quedan menos personas, la cantidad de personas alcanzadas por un rayo cada año disminuye, ya que esa misma probabilidad se aplica sobre un número cada vez menor de personas.

Si tu objetivo es predecir la población, es inconveniente utilizar la probabilidad, pero tampoco puedes usar una tasa porque siempre está cambiando, ya que depende de la población.

Eso es lo que resuelve la vida media. Es bastante fácil de medir, intuitivo de usar, y permanece igual incluso a medida que la población cambia y sigue siendo válido mientras la población sea estadísticamente grande.

Supongamos que la probabilidad de que alguien sea asesinado por un rayo es extremadamente mortal, 5% cada año. Al final del primer año, solo queda el 95% de las personas originales. Pero en el segundo año, la probabilidad no ha cambiado y todavía es del 5%. Por lo tanto, ahora ese 5% se aplica a las personas restantes. No importa cuántas personas comenzaste. Lo único que importa es cuántas personas tienes en este momento. En lugar de usar el 5% durante un año, podrías optar por acumular esa probabilidad durante un cierto número de años donde la probabilidad acumulativa para cualquier persona será del 50%. En este caso, serían 13.5 años. Eso es lo que significa la vida media. Cada 13.5 años, la mitad de tu población al comienzo desaparece.

Sin embargo, si reduces suficientemente la población, en algún momento ya no habrá una probabilidad cercana al 100% de que algún número distinto de cero de personas sean alcanzadas por un rayo durante el próximo año. Ese es el punto en el que la naturaleza estadística de la vida media ya no se puede aplicar. En la práctica, dejará de ser válido en algún momento.

Otra consecuencia de que la población sea muy grande (como el número de átomos) es que habrá algunos átomos muy, muy afortunados entre ellos que pueden sobrevivir durante mucho tiempo. Puede ser una posibilidad de uno en un trillón de trillones de trillones de que un átomo específico pueda sobrevivir a todos esos intervalos de vida media, pero tienes muchas magnitudes más de átomos que eso. Después de muchos intervalos de vida media, cuando tienes estos átomos de larga vida frente a ti, nunca sabes cuánto tiempo más durará uno en particular; la probabilidad de que cada uno sobreviva al siguiente intervalo de vida media nunca ha cambiado. Pero lo que sí sabes es que sobrevivieron a todos los intervalos de vida media anteriores porque todavía están frente a ti. Pero si todavía hay suficientes de ellos frente a ti para tratarlos estadísticamente, eso significa que hay una gran cantidad de átomos aún más afortunados escondidos en la multitud que sobrevivirán a muchos más intervalos de vida media. Es por eso que el número de átomos restantes es matemáticamente asintótico, pero como mencioné, cuando la población se vuelve lo suficientemente pequeña, ya no se puede tratar estadísticamente.

Con suerte, esto ilustra cómo la descomposición no es un "n cantidad de átomos que se desintegran cada minuto" sino más bien una "probabilidad de que un átomo específico se desintegre" traducida a una métrica macroscópica cuando la población es lo suficientemente grande como para tratarse estadísticamente.

Answer 3

Es casi como si los átomos en una muestra de alguna manera 'supieran' cuántos otros átomos hay en la muestra.

Esta es la clave. De hecho, es exactamente lo contrario, es precisamente porque no saben cuántos otros átomos hay en la muestra que la vida media es constante.

Las curvas de supervivencia no solo ocurren con átomos, ocurren con todo tipo de objetos. Puedes pensar en el número de conejos en una población que mueren, o en el número de un tipo de piezas de automóvil que fallan, y así sucesivamente. Estas cosas generalmente no tienen tasas de falla constantes, o vidas medias.

Las tasas de falla de las piezas de automóvil tienden a ser altas para piezas nuevas, algunas piezas se rompen en las primeras cien horas debido a defectos de fabricación. Luego la tasa de falla se estabiliza y se vuelve constante, casi como una vida media constante. En este rango es solo una lotería al azar, con cada parte jugando el juego cada hora que se utiliza, con igual probabilidad de que cada parte falle en cualquier hora dada que se use. Luego, la tasa de falla comienza a aumentar nuevamente a medida que las piezas se desgastan mecánicamente. Fallan a una tasa más alta hacia el final de su vida útil. Entonces la tasa de falla no es constante a medida que la parte "envejece".

De manera similar, los conejos adultos sanos pueden vivir con una baja tasa de falla si hay un número modesto de conejos en la población. Cada conejo tiene esencialmente una probabilidad aleatoria independiente de morir cualquier día. Pero si hay demasiados, mueren con más frecuencia por inanición o si hay muy pocos conejos en la población, entonces mueren a una tasa mucho más alta por depredación. Entonces su tasa de muerte individual depende del número de otros conejos.

Los átomos no son como los coches. No hay átomos defectuosos y no se desgastan, solo tienen esa parte media constante. Los átomos tampoco son como los conejos, no les importa cuántos son. No hay un ajuste basado en la edad o población a la tasa de descomposición aleatoria constante.

Entonces, ¿por qué la vida media es constante? Es porque los átomos de un tipo particular son todos idénticos.

Answer 4

Digamos que tienes solo 4 átomos radiactivos con una vida media de 1 hora. . . . . . Por lo tanto, esto significa que 1 hora a partir de ahora, 2 de los átomos se habrán desintegrado (en promedio) y 2 permanecerán sin desintegrarse (en promedio).
Esa palabra promedio es la palabra que has malinterpretado.

Existe una probabilidad finita de que los cuatro átomos se desintegren en 1 hora y es de $1/2 \times 1/2 \times 1/2 \times 1/2=1/16$.
La probabilidad de que los cuatro no se desintegren en 1 hora es de $1/2 \times 1/2 \times 1/2 \times 1/2=1/16$.

La probabilidad de que solo uno se desintegre en una vida media es un poco más difícil de calcular.
Etiquetando los átomos como $\mathbf {a,\,b,\,c,\,d}$, entonces la probabilidad de que el átomo $\mathbf a$ se desintegre y los demás no lo hagan es de $1/2 \times 1/2 \times 1/2 \times 1/2=1/16$.
La probabilidad es la misma si solo uno de los otros átomos se desintegra, por lo que la probabilidad de que solo un átomo se desintegre dentro de una vida media es de $4\times 1/16 = 1/4$.

Ahora llegamos a un resultado interesante para la probabilidad de que dos átomos se desintegren en una vida media, ¿no debería ser de $1/2$?
La probabilidad de que solo $\mathbf a$ y $\mathbf b$ se desintegren en una vida media es de $1/16$, pero lo que se necesita es la probabilidad de que cualquier par de átomos se desintegre en una vida media.
Entonces lo que se necesita es el número de formas en que se pueden elegir dos elementos de cuatro elementos y hay seis formas: $\{\mathbf {a,b}\}, \, \{\mathbf {a,c}\}, \,\{\mathbf {a,d}\}, \,\{\mathbf {b,c}\}, \,\{\mathbf {b,d}\}, \,\{\mathbf {c,d}\}$.
Así que la probabilidad de que solo 2 átomos se desintegren es de $6\times 1/16 = 3/8$.
Por lo tanto, que solo se desintegren dos átomos en una vida media es el evento más probable, pero no ocurre la mitad del tiempo.

Que solo tres átomos se desintegren en una vida media requiere el número de formas de elegir tres elementos de cuatro $(4)$ y por lo tanto, la probabilidad de que tres átomos se desintegren en una vida media es de $4\times 1/16 = 1/4$.

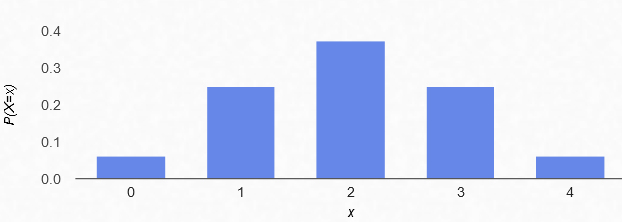
Entonces, la distribución de probabilidad para un número $x$ de átomos que se desintegran a partir de un número original de cuatro átomos se ve así,

Para encontrar el número promedio de desintegraciones en una vida media, es necesario calcular un promedio ponderado, que en este caso es de $(1/16 \times 0) + (1/4 \times 1) +(3/8 \times 2) +(1/4 \times 3) +(1/16 \times 4) = \mathbf 2$ y ahí está el número esperado de átomos que se desintegran en una vida media, $\mathbf 2$.

Continuando.
. . . Me cuesta entender por qué los últimos 2 átomos no desintegrados, en promedio, se desintegrarán ambos en la siguiente hora.
Usando las ideas utilizadas anteriormente, se encuentra que la probabilidad de que ningún átomo se desintegre en una vida media es de $1/4$, que un átomo se desintegre es de $1/2$ y que ambos átomos se desintegren es de $1/4$ con un promedio ponderado de un átomo desintegrándose en una vida media.
Entonces, ¿por qué el promedio no es de dos? Es porque hay otros dos modos de descomposición, ninguno de los cuales se descompone y uno de ellos se descompone, que también deben tenerse en cuenta.

Otra idea importante es que la probabilidad de que exactamente la mitad de los átomos se desintegren en una vida media es muy pequeña. De hecho, para $10,000$ núcleos inestables, la probabilidad de que exactamente $5,000$ se desintegren durante una vida media es de $0.007979$.

La distribución de probabilidad que he utilizado indirectamente se llama la distribución binomial y hay muchos calculadores de distribución binomial disponibles, de los cuales te doy uno enlace y enlace dos, pero ten en cuenta que hay muchos otros.

Answer 5

Los átomos solo tienen algunas propiedades distintivas como el número de protones, neutrones, electrones y sus niveles de energía. Los átomos que tienen estas mismas pocas propiedades son idénticos e indistinguibles entre sí. La "edad" de un átomo no es una propiedad distintiva, un átomo recién formado en una reacción nuclear puede ser completamente indistinguible de uno que ha estado presente durante milenios. Los átomos no tienen "memoria" o alguna propiedad que pueda capturar algo como "tiempo hasta la descomposición".

Esta propiedad indica que la descomposición radioactiva debe seguir una distribución exponencial, que tiene un porcentaje fijo de eventos en cada período de tiempo. En una vida media, cada átomo tiene un 50% de probabilidad de descomposición. De los que quedan, tienen un 50% de probabilidades de descomponerse en la siguiente vida media, y un 50% después de eso, y después de eso. Si ves que el 50% de los átomos se descompone en la primera vida media y luego el 100% de los restantes se descompone en la segunda vida media, implicaría que esos átomos restantes "sabían" que habían sobrevivido más tiempo, ya que exhibirían una tasa de descomposición dependiente del tiempo. Pero nuestra premisa básica es que las propiedades de un átomo no son dependientes del tiempo; un átomo nuevo y uno viejo no se pueden distinguir.

La distribución exponencial puede ser un poco contraintuitiva ya que muchas cosas exhiben una supervivencia dependiente de la edad, como los seres vivos, la electrónica, los edificios, etc. - a medida que envejecen, generalmente se vuelven más propensos a fallar. Todas estas cosas tienen algún mecanismo de "desgaste" que codifica físicamente la historia del objeto y los hace más propensos a fallar a medida que envejecen. Esto no es válido para los átomos, un átomo no puede "desgastarse" o codificar su propia historia de alguna manera. Con la supervivencia dependiente de la edad, a menudo es cierto que cada día te acerca más a la muerte, ya que tu probabilidad de muerte aumenta con el tiempo. Pero un átomo que sobrevive a una vida media no está más cerca de la "muerte" que cuando comenzó - un átomo que ha sobrevivido a un millón de vidas medias tiene exactamente la misma expectativa de vida hacia adelante que un átomo recién creado. Un ejemplo intuitivo de la distribución exponencial es tus probabilidades de ganar la lotería asumiendo que juegas cada día. Si juegas lo suficiente, eventualmente ganarás, pero jugar cada día no te acerca más a ganar - haber jugado y perdido todos los días durante 10 años no te hace más probable ganar que a alguien que compra su primer boleto de lotería.

Si un átomo en particular tiene un 50% de probabilidad de descomposición en un período de tiempo, también lo hacen todos los demás átomos de ese tipo. Si esto no fuera así, contradiría la idea de que los átomos son indistinguibles entre sí.