Pruebas contundentes de que dos puntos de base son mejores que uno

Question

Esta pregunta se inspira en una respuesta de Tim Porter .

Ronnie Brown fue pionero en la creación de un marco para la teoría de la homotopía en el que se pueden considerar múltiples puntos de base. Estas ideas se presentan de forma accesible en su libro Topology and Groupoids. La idea del grupo fundamental, presentada como una alternativa de múltiples puntos base al grupo fundamental, es el punto culminante de la teoría. El resultado principal parece ser que el Teorema de van-Kampen parece más natural en el contexto de los groupoides.
No sé si este resultado del titular me convence, ya que la carga adicional de los grupúsculos y los empujones me hace cuestionar si la recompensa merece la pena, sobre todo porque soy una persona de topología geométrica, más que un teórico de la homotopía.

¿Tiene usted ejemplos en topología geométrica (3 manifolds, 4 manifolds, marañas, trenzas, nudos y enlaces...) en los que el concepto de groupoide fundamental haya sido útil, en el sentido de que haya conducido a nuevos teoremas o a un tratamiento sustancialmente simplificado de temas conocidos?

Un lugar en el que puedo imaginar (pero, por falta de pruebas, sólo imaginar) que los groupoides fundamentales podrían ser útiles (al menos para simplificar la exposición) es en la teoría de los nudos, donde cambiamos constantemente entre (al menos) tres opciones "naturales" diferentes de punto base: en el propio nudo, en el límite de una vecindad tubular y en el complemento del nudo. Este cambio de punto base añade una desagradable complejidad técnica con la que he tenido que luchar al escribir artículos. Una prueba reciente (Proposición 8 de mi papel con Kricker ) que habrían sido unas pocas líneas si no hubiéramos tenido que preocuparnos por los puntos de base, se convirtieron en 3 páginas. En otra dirección, ¿qué pasa con los grupos fundamentales de las trenzas?
¿Se han explorado las ideas de los groupoides fundamentales en contextos topológicos geométricos? Y si no, ¿por qué no?

Answer 1

La siguiente imagen ilustra una situación de intersecciones no inusual, en la que se supone que los distintos componentes tienen varios grupos fundamentales:

Aquí ayuda tener un teorema que determina inmediatamente el grupo fundamental de la unión en estos puntos base. Luego se utiliza el álgebra y la combinatoria para elaborar grupos fundamentales particulares, si se quiere.

Llegué a los groupoides tratando de encontrar una nueva prueba del grupo fundamental del círculo. Resultó que se podía hacer esto utilizando el groupoide fundamental en dos puntos base. Un ejemplo análogo, con una cobertura universal no tan obvia, es el espacio no Hausdorff $X$ obtenido de $[-1,1]\times \{-1,1\}$ identificando todos los $(t, 1)$ con $(t, -1)$ , excepto en el caso de $t=0$ como en la siguiente imagen:

Escribir la edición de 1968 de mi libro ahora llamado Topología y Groupoides (T&G) (disponible en amazon.com y en versión electrónica en mi sitio web) me convenció de que toda la teoría de la homotopía unidimensional se expresaba mejor en términos de groupoides en lugar de grupos, ya que se obtenían teoremas más potentes con pruebas más sencillas. Los resultados posteriores sobre el groupoide fundamental de los espacios orbitales (capítulo 11 de T&G) son más incómodos de expresar en términos de grupos; esto desarrolla el punto de Dustin Clausen. Véanse más detalles a continuación.

Henry Whitehead respondió a la pregunta de "¿Por qué no restringir a los complejos CW con un solo vértice?" considerando los espacios de cobertura. Philip Higgins dio una considerable generalización del teorema de Grusko considerando morfismos de cobertura de los groupoides, véase su libro de 1971 `Categories and groupoids' disponible como Reimpresión del TAC, 2005 .

En 1966 pensé en los posibles usos de los groupoides en la teoría de la homotopía superior, y esto condujo durante muchos años a los Teoremas de Seifert-van Kampen de dimensión superior, con una serie de nuevos cálculos noabelianos de grupos de homotopía relativa segunda y grupos de homotopía tríada (para este último, véase el "producto tensorial noabeliano de grupos"). Esto parece relevante para la topología geométrica.

Así que una respuesta a la pregunta original es que el uso de los groupoides abre nuevos mundos de posibilidades.

En realidad, la idea del "cambio de punto de partida para el grupo fundamental" es un poco extraña: ¡no se describe un horario ferroviario en términos de viajes de ida y vuelta y de cambio de punto de partida para estos! ¿Por qué se sigue enseñando esto a los estudiantes?

Al final, un punto de vista estético implica más poder.

Gracias a los de arriba que me dan ejemplos adicionales.

Más información en mi página De los grupos a los groupoides .

Septiembre de 2012: Se me olvidó añadir a esta respuesta más información sobre espacios orbitales con especial referencia a los "dos puntos de base".

Ross Geoghegan, en su reseña de 1986 (MR0760769) de dos artículos de M.A. Armstrong sobre los grupos fundamentales de los espacios orbitales, escribió: "Estos dos artículos muestran qué partes de la teoría elemental de los espacios de cobertura se trasladan del caso libre al caso no libre. Este es el tipo de material básico que debería haber estado en los libros de texto estándar sobre grupos fundamentales durante los últimos cincuenta años". En la actualidad, que yo sepa, "Topology and Groupoids" es el único texto de topología que recoge estos resultados.

Consideremos la acción del grupo cíclico de orden 2, $Z_2$ en el círculo unitario $S$ por conjugación compleja. Tome $1$ como punto base. La acción inducida de $Z_2$ en el grupo fundamental $\pi_1(S,1)$ es $n\mapsto -n$ y el cociente por esta acción es $Z_2$ . Pero el cociente de $S$ por la acción es un semicírculo, que es contraíble. ¿Qué ha salido mal?

El problema es que hay dos puntos fijos de la acción. El cociente de la acción de $Z_2$ en el grupúsculo $\pi_1(S, A)$ , donde $A$ se compone de los puntos $\pm 1$ es, en efecto, correcto.

La cuestión es que un grupo que actúa sobre un espacio $X$ actúa también sobre el grupo fundamental $\pi_1 X$ . Si $X$ es Hausdorff, la acción es propiamente discontinua, y $X$ tiene una cobertura universal, entonces el grupo fundamental del espacio orbital $X/G$ es el grupo orbital de $\pi_1 X$ . Esta es la expresión grupal de los resultados de Armstrong. Véase el capítulo 11 de Topología y Groupoides .

21 de abril de 2013: El libro Topología algebraica no abeliana: espacios filtrados, complejos cruzados, groupoides homotópicos cúbicos da cuenta de este nuevo enfoque de la topología algebraica básica en la frontera entre la homología y la homotopía, sin utilizando la teoría de la homología singular, o la aproximación simplicial, pero apoyándose en la idea de composiciones múltiples de cubos. Esto también permite obtener resultados sobre los segundos grupos de homotopía relativa, resultados que, al ser esencialmente no abelianos, no se pueden obtener mediante la topología algebraica tradicional. También evita el "truco" de tomar el grupo abeliano libre sobre símiles ordenados u orientados para definir grupos de cadenas, y el mapa de límites.

Obsérvese que, mientras que los objetos de grupo internos a los grupos son grupos abelianos, los objetos de grupo internos a los groupoides son, en cierto sentido, "más no abelianos" que los grupos, al igual que los objetos de groupoide internos a los groupoides. Por tanto, se busca que tales objetos modelen propiedades de homotopía superior: y esto se ha conseguido.

2 de octubre de 2014: Di una charla sobre las "Intuiciones para los métodos cúbicos en topología algebraica no abeliana" en el PHI, París, en junio de 2014 a un taller sobre "Matemática constructiva y modelos de teoría de tipos", y la versión de mano de las diapositivas está disponible ici . Para mí, una de las principales ventajas de la excursión a los groupoides es que me llevó a pensar en versiones superiores y en cómo expresar algunas intuiciones clave. La pregunta general era:

"Si los groupoides son muy útiles en $1$ -dimensionales, ¿pueden ser útiles, o no, en la homotopía superior?"

11 de marzo de 2015

Espero que las observaciones de Grothendieck enlazadas aquí como puntos base se encuentran interesantes.

Aug 4, 2015 Una discusión relacionada se encuentra en mathstackexchange .

15 de septiembre de 2015. acaban de encontrar este documento:

arXiv:1508.03122 "Dynamics on Wild Character Varieties" Emmanuel Paul, Jean-Pierre Ramis Journal-ref: SIGMA 11 (2015), 068, 21 páginas

Es relevante, ya que utiliza el groupoide fundamental sobre un conjunto de puntos base en el contexto no de la topología algebraica, sino de los sistemas dinámicos y las ecuaciones diferenciales.

19 de septiembre: Otro punto que se desprende del documento de Paul-Ramis es la utilidad de preservar la información de simetría. Como otro ejemplo, consideremos la siguiente unión conectada de tres espacios, con un conjunto $S$ de los puntos base elegidos:

Una descripción de $\pi_1(X,S)$ preservará las simetrías de la situación, y esta descripción puede ser necesaria para posteriores investigaciones.

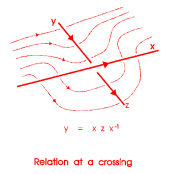
12 de julio. 2017 Con respecto al punto de Daniel sobre los nudos, la siguiente imagen

permite intuir la relación $y=xzx^{-1}$ en un cruce de un diagrama de nudos. En realidad, es una imagen de un grupo, y me parecería más oscura si se intentara convertirla en una imagen sobre bucles. Para mantenerlo, se podrían utilizar dos puntos base por cruce, uno para "entrar" en la parte superior izquierda y otro para "salir" en la parte superior derecha. ¡Dejo que otros vean si esta es una idea útil!

Philip Higgins me habló de una frase de su supervisor Philip Hall: "Hay que tratar de encontrar un álgebra que modele la geometría, y no forzar la geometría en un modo algebraico particular simplemente porque ese modo es más familiar".

Hay más antecedentes en mi artículo de 2018 sobre Indagationes Modelización y cálculo de tipos de homotopía: I .

Octubre de 2019

Las ideas de muchos puntos base para definir los groupoides fundamentales también son relevantes para la historia de la teoría de la homotopía, lo que se puede confirmar en los libros de historia de la topología (Dieudonn'e, James). En 1932 E. Cech impartió un seminario en el ICM de Zúrich sobre "Grupos de homotopía superiores". Los definió y también demostró que eran abelianos para $n \geqslant 2$ . En aquella época, un interés general entre los topólogos era encontrar una versión de mayor dimensión del grupo fundamental, que por supuesto era en general no abeliano. Así que los reyes de la topología de la época, Aleksandrov y Hopf, argumentaron que la definición de Cech no podía ser la "correcta"; sólo apareció un pequeño párrafo en las Actas, y Cech no volvió a trabajar sobre el tema.

Más tarde, el interés surgió con la publicación en 1935 de los trabajos de Hurewicz, y el estudio de los grupos de homotopía se convirtió en una parte central de la topología algebraica. Conocemos la naturaleza abeliana de estos grupos como resultado de "los objetos de los grupos son abelianos abelianos". La idea de versiones de mayor dimensión del grupo fundamental se descartó en cierto modo, aunque Henry Whitehead mencionó en mi audiencia de 1957 que los primeros teóricos de la homotopía estaban fascinados por la acción del grupo fundamental.

Sin embargo, Aleksandrov y Hopf seguramente tenían razón. Ahora sabemos que los "groupoides en la categoría de los groupoides" pueden ser más complicados que los groupoides, y así sucesivamente en dimensiones superiores. La fascinación por el estudio de los grupos de homotopía, que sólo se definen para los espacios con punto base, parece haber sido un factor para ignorar la idea de un conjunto de puntos base. La posible definición de grupos de homotopía superior estrictos parece necesitar más estructura en un espacio, por lo que se ha trabajado mucho en el estudio de grupos de homotopía superior no estrictos. Para una parte de la historia del caso estricto, véase mi artículo de 2018 Indagationes documento mencionado anteriormente.

1 de octubre de 2020

Espero que el siguiente archivo Grothendieck de una presentación de Beamer de una charla para una conferencia de zoom sobre Grothendieck organizada por John Alexander Cruz Morales y Colin McLarty para el 27-28 de agosto de 2020 será útil: contiene una extensa cita de los comentarios de Grothendieck de mi De los grupos a los groupoides artículo de estudio y también sugerencias de relaciones con los groupoides de Conway, y de usos de digamos miles de puntos base.

Answer 2

He aquí un ejemplo interesante en el que los groupoides son útiles. El grupo de clases de mapeo $\Gamma_{g,n}$ es el grupo de clases de isotopía de difeomorfismos que preservan la orientación de una superficie de género $g$ con $n$ puntos marcados distintos (etiquetados del 1 al n). El espacio de clasificación $B\Gamma_{g,n}$ es homología racional equivalente al espacio de moduli (grueso) $\mathcal{M}_{g,n}$ de curvas complejas de género $g$ con $n$ puntos marcados (y si estás dispuesto a hablar del orbifold o pila de moduli, entonces es realmente una equivalencia de homotopía)

El grupo simétrico $\Sigma_n$ actúa sobre $\mathcal{M}_{g,n}$ permutando las etiquetas de los puntos marcados.

Pregunta: Cómo describimos la correspondiente acción del grupo simétrico sobre el espacio clasificador $B\Gamma_{g,n}$ ?

Es posible ver $\Sigma_n$ como actuando por automorfismos externos en el grupo de clases de mapeo. Supongo que probablemente se podría construir una acción sobre el espacio clasificatorio directamente a partir de esto, pero aquí hay una forma mucho más agradable de manejar el problema.

El grupo $\Gamma_{g,n}$ puede identificarse con el grupo fundamental del orbifold del espacio de moduli. Sustituyámoslo por un groupoide fundamental. Fijemos una superficie $S$ con $n$ puntos distinguidos, y tomamos el grupito donde los objetos son etiquetados de los puntos distinguidos por 1 a n, y los morfismos son clases de isotopía de difeomorfismos que respetan los etiquetados (es decir, enviando el punto etiquetado $i$ en el primer etiquetado hasta el punto etiquetado $i$ en el segundo etiquetado).

Es evidente que este grupo es equivalente al grupo de la clase de mapeo original, por lo que su espacio de clasificación es equivalente a la homotopía. Pero ahora tenemos una acción honesta del grupo simétrico permutando las etiquetas de los puntos distinguidos de $S$ .

Answer 3

Una de las situaciones en las que es imprescindible utilizar los groupoides es el estudio de los orbifolds.

Eslogan: El conjunto de puntos de un orbifolio es un grupito.

---

He aquí un problema concreto que se ilumina con el lenguaje de los groupoides. Supongamos que tengo un orbifold $M$ con un estrato singuar $X$ . El estrato $X$ es isomorfo a $S^1$ y su grupo de isotropía es algún grupo finito $G$ . Supongamos también que $X$ está orientado.

Pregunta: ¿Cuál es la "monodromía" de rodear ese estrato?

A primera vista, uno podría adivinar que se trata de un elemento de $Aut(G)$ .
¡Eso está mal! La monodromía es un elemento de $Out(G)$ .
Así que tenemos ante nosotros una situación un tanto paradójica: hay un grupo asociado a cada punto de $X$ . Sin embargo, la monodromía no actúa por automorfismos de ese grupo.

Este es un ejemplo de orbifold que ilustra muy bien el tipo de situación que puede darse: $$ M = (S^1\times V )/S_n, $$ donde $S_n$ es el grupo simétrico y $V$ es una representación fiel. El grupo $S_n$ actúa sobre el círculo $S^1$ a través de la proyección $S_n\twoheadrightarrow\mathbb Z_2$ y luego el mapa antipodal. La representación $V$ de $S_n$ sólo se pone ahí para que el orbifold no sea demasiado degenerado (se puede omitir si no te importa trabajar con orbifolds no efectivos).

En ese ejemplo, el colector $X$ es $S^1/\mathbb Z_2$ . El grupo de isotropía es el grupo alterno $A_n$ . La monodromía se calcula de la siguiente manera. Recorrer la mitad del camino $S^1$ y luego identificar " $A_n$ en el punto -1" con " $A_n$ en el punto +1" a través de cualquier elemento de $S_n$ que envía -1 a +1. La elección de un elemento de este tipo da lugar a un automorfismo de $A_n$ . Pero como no existe la mejor manera de hacer tal elección, lo único canónico es su clase en $Out(A_n)$ .

Bien. Tal vez sea un buen momento para intentar eliminar parte de la confusión.
Todo queda más claro una vez que te das cuenta de que lo que se asocia a un punto de $X$ no es un grupo. Es un groupoide:

Si $[M/G]$ es un orbifold y $x$ es un punto en $M/G$ , entonces el groupoide que vive encima de $x$ tiene objetos dados por puntos $m\in M$ asignación a $x$ . Una flecha de $m$ a $m'$ viene dada por un elemento de $G$ que envía $m$ a $m'$ .

La monodromía es entonces simplemente un automorfismo de ese groupoide (así que ahora ya no hay nada raro). Pero este automorfismo puede no fijar ninguno de los objetos del grupito. Y por tanto no puede ser visto como un automorfismo del grupo correspondiente, a no ser que hagas algunas elecciones poco naturales.

Answer 4

Me gustaría ampliar el punto de Dustin. Simplemente no hay manera de pensar con sentido sobre la topología equivariante, ya sea algebraica o geométrica, sin tener en cuenta múltiples puntos base. Incluso teniendo en cuenta que uno se encuentra con dificultades sutiles invisibles sin ellas (véase, por ejemplo, [65] en mi página web ). Daré ejemplos de topología algebraica, ya que es lo que mejor conozco, pero los ejemplos de topología geométrica topología geométrica deben abundar, como se ilustra en otras respuestas.

Tomemos un grupo de Lie compacto, o incluso sólo un grupo finito, y consideremos un grupo cerrado y liso $G$ -manifold $M$ . ¿Qué significa para $G$ para ser orientable, y ¿qué es una orientación? Estos son preguntas muy interesantes, necesarias para dar sentido de la dualidad equivariante de Poincar, y son difíciles excepto en el caso aburridamente simple (tratado en [53] sobre mi sitio web ) cuando la tangente $G_x$ -representación $T_x$ es es isomorfo a la restricción a $G_x$ de un ambiente $G$ -representación $V$ para todos $x\in M$ . Normalmente no hay tal $V$ y entonces no puedo imaginar respuestas que no utilicen funtores definidos en groupoides fundamentales equivariantes (Tres referencias que dan respuestas bastante diferentes a estas preguntas son [93] y [100] sobre preguntas son [93] y [100] sobre mi sitio web y Homología y cohomología ordinaria equivariante de Costenoble y Waner. En realidad no sé cómo comparar estas respuestas o calcular con ellas.

Una vez más, aunque se puede escapar (retorcidamente) del uso explícito de la fundamentales al establecer la secuencia espectral de Serre con coeficientes locales local, no se puede hacer de forma equitativa.

Tal vez invocar la teoría equivariante sea una exageración, pero el groupoide fundamental es algo tan natural, y tan elemental, que parece un poco perverso intentar evitarlo.

Answer 5

Un breve ejemplo.

La familia de grupos trenzados puros no posee una estructura de operada simétrica.

Pero el grupo fundamental de la pequeña operada de 2 discos es naturalmente una operada simétrica.

Aunque los grupos fundamentales de la pequeña ópera de 2 discos son los grupos puros de la trenza, no hay forma de elegir puntos de base consistentes con la estructura de la ópera.

La moraleja es que los groupoides no son naturalmente puntuales, mientras que los grupos sí lo son. Si trabajas con grupos fundamentales, deberías trabajar con espacios puntuales. Por supuesto, puedes ignorar esto y sólo tendrás problemas si tus matemáticas no funcionan con espacios puntuales, como en el ejemplo anterior.