A la pregunta "¿qué es la impedancia?", yo señalaría que la impedancia es un concepto amplio de la física en general, del que la impedancia eléctrica es sólo un ejemplo.
Para entender lo que significa y cómo funciona, suele ser más fácil considerar la impedancia mecánica. Piensa en intentar empujar (deslizar) un sofá pesado por el suelo.
Aplicas una determinada fuerza y el sofá se desliza a una determinada velocidad, dependiendo de la fuerza con la que empujes, el peso del sofá, el tipo de superficie del suelo, el tipo de pies que tenga el sofá, etc. Para esta situación, es posible definir una impedancia mecánica que da la relación entre la fuerza con la que empujas y la velocidad con la que se desliza el sofá.
En realidad, se parece mucho a un circuito eléctrico de corriente continua, en el que se aplica una determinada cantidad de tensión a través de un circuito, y la corriente fluye a una determinada velocidad correspondiente a través de él.
Tanto en el caso del sofá como en el del circuito, la respuesta a tu entrada puede ser simple y bastante lineal: una resistencia que obedece a la Ley de Ohm, donde su impedancia eléctrica es sólo la resistencia, y el sofá puede tener pies deslizantes de fricción que le permiten moverse con una velocidad proporcional a tu fuerza.*
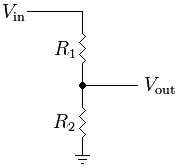
Los circuitos y los sistemas mecánicos también pueden ser no lineales. Si el circuito consiste en una tensión variable colocada a través de una resistencia en serie con un diodo, la corriente será casi nula hasta que se supere la tensión directa del diodo, momento en el que la corriente comenzará a fluir a través de la resistencia, de acuerdo con la ley de Ohm. Del mismo modo, un sofá sentado en el suelo suele tener cierto grado de fricción estática: no empezará a moverse hasta que se empuje con una cierta fuerza inicial. Ni en el sistema mecánico ni en el eléctrico hay una única impedancia lineal que pueda definirse. Más bien, lo mejor que se puede hacer es definir por separado las impedancias en diferentes condiciones. (El mundo real es mucho más parecido a esto).
Incluso cuando las cosas son muy claras y lineales, es importante tener en cuenta que la impedancia sólo describe una relación, no describe los límites del sistema, y no es "mala". Definitivamente, puedes obtener toda la corriente/velocidad que quieras (en un sistema ideal) añadiendo más voltaje/empujando más fuerte.
Los sistemas mecánicos también pueden dar una idea bastante buena de la impedancia de la corriente alterna. Imagina que vas en bicicleta. Con cada medio ciclo de los pedales, empujas a la izquierda, empujas a la derecha. También puedes imaginar que pedaleas con un solo pie y una pinza, de forma que empujas y tiras con cada ciclo del pedal. Esto se parece mucho a la aplicación de un voltaje de corriente alterna a un circuito: se empuja y se tira a su vez, cíclicamente, a una determinada frecuencia.
Si la frecuencia es lo suficientemente lenta, como cuando estás parado en la bicicleta, el problema de empujar los pedales hacia abajo es sólo un problema de "dc", como empujar el sofá. Sin embargo, cuando se acelera, las cosas pueden actuar de forma diferente.
Supongamos que vas en bicicleta a cierta velocidad y que tu bicicleta es de tres velocidades con relaciones de cambio bajas, medias y altas. La relación media se siente natural, la alta es difícil de aplicar la fuerza suficiente para hacer alguna diferencia, y en la relación baja, sólo giras los pedales sin transferir ninguna energía a las ruedas. Esto es una cuestión de adaptación de la impedancia En este caso, sólo se puede transferir eficazmente la potencia a las ruedas cuando éstas presentan una cierta resistencia física al pie, ni demasiado ni demasiado poco. El fenómeno eléctrico correspondiente también es muy común; se necesitan líneas de impedancia adaptada para transmitir eficazmente la potencia de radiofrecuencia del punto A al punto B, y cada vez que se conectan dos líneas de transmisión, habrá alguna pérdida en la interfaz.
La resistencia que ofrecen los pedales a tus pies es proporcional a la fuerza con la que pisas, lo que lo relaciona más con una resistencia simple, sobre todo a bajas velocidades. Incluso en los circuitos de corriente alterna, una resistencia se comporta como una resistencia (hasta cierto punto).
Sin embargo, a diferencia de una resistencia, la impedancia de una bicicleta depende de la frecuencia. Supongamos que pones la bicicleta en una marcha alta, partiendo de una parada. Puede ser très difícil de empezar. Pero, una vez que empiezas, la impedancia presentada por los pedales disminuye a medida que vas más rápido, y una vez que vas muy rápido, puedes encontrar que los pedales presentan muy poca impedancia para absorber la energía de tus pies. Así que en realidad hay una impedancia que depende de la frecuencia (a reactancia ) que comienza alto y se va reduciendo a medida que se avanza en la frecuencia.
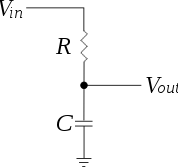
Esto es muy parecido al comportamiento de un condensador, y un modelo bastante bueno para la impedancia mecánica de una bicicleta sería una resistencia en paralelo con un condensador.
En corriente continua (velocidad cero), sólo ves la resistencia alta y constante como tu impedancia. A medida que la frecuencia de pedaleo aumenta, la impedancia del condensador se vuelve más baja que la de la resistencia, y permite que la corriente fluya en esa dirección.
Hay, por supuesto, otros componentes eléctricos y sus analogías mecánicas**, pero esta discusión debería darte una intuición inicial sobre el concepto general para que tengas los pies en la tierra (juego de palabras) mientras aprendes sobre los aspectos matemáticos de lo que a veces puede parecer un tema muy abstracto.
*Una palabra para los quisquillosos: la ley de Ohm nunca es exacta para un dispositivo real, y las fuerzas de fricción del mundo real nunca dan una velocidad exactamente proporcional a la fuerza. Sin embargo, "bastante lineal" es fácil. Estoy tratando de ser todo educativo y esas cosas aquí. No me hagas caso.
**Por ejemplo, un inductor es algo así como un rodillo con muelle en la rueda que añade resistencia a medida que se llega a una frecuencia más alta)