¿Por qué la radiación bajo el arrastre de Poynting-Robertson es anisotrópica?

Question

Según la Artículo de la Wikipedia sobre el arrastre de Poynting-Robertson La razón por la que la radiación solar ralentiza un objeto en órbita es porque la re-radiación de fotones por el objeto es anisotrópica en el marco de la estrella, como se muestra en esta imagen:

Pero, ¿por qué esa radiación sería anisotrópica? ¿No irradiarían los electrones del objeto la luz de forma más o menos aleatoria, sobre todo si el objeto no fuera muy reflectante o liso?

Answer 1

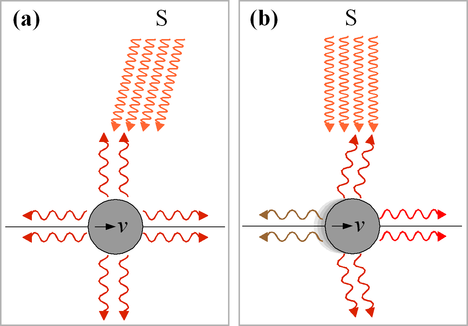
Ellos hacer irradian luz al azar en todas las direcciones -- en el propio marco de referencia del objeto . Pero no desde el marco de referencia del Sol. El efecto en general se denomina "haz relativista".

Esta es la derivación más clara que conozco. Tomemos las matrices de Pauli $\sigma_i$ y adjuntarles la matriz identidad como $\sigma_0 = I$ . Ahora toma un cuatro-vector $v^\mu$ y formar la matriz hermitiana 2x2 $V = \sigma_\mu v^\mu.$ Puede demostrar que de hecho $\det V = v_\mu v^\mu$ dans le $(+\,-\,-\;-)$ métrica, con $\operatorname{Tr}V = 2 v^0.$ Por lo tanto, las transformadas de Lorentz conservan los determinantes; podemos clasificarlas como las transformadas "especiales" de Lorentz $V \mapsto L V L^\dagger$ con $\det L = \pm 1,$ donde el $-$ no importa y se puede ignorar con seguridad, y algunas otras operaciones que no se pueden hacer de esta manera, como la 4-reversión $V\mapsto -V$ o la transformación de paridad $V \mapsto (\det V) ~ V^{-1},$ que invierte el signo de los índices espaciales pero no el del índice temporal.

Eso no estará del todo claro después de leer sólo un párrafo, pero realmente empieza a escribir la expresión para $V$ , $$V = \begin{bmatrix}v^0 + v^3 & v^1 -i v^2\\v^1 + i v^2 & v^0 - v^3\end{bmatrix}$$ y derivar, por ejemplo, que la transformada de Lorentz de un impulso con rapidez $w = \tanh^{-1}\beta$ dans le $+z$ -la dirección es $$L = \begin{bmatrix}e^{w/2}&0\\0&e^{-w/2} \end{bmatrix},$$ mientras que las matrices unitarias proporcionan rotaciones, etc., y lo conseguirás muy pronto.

Supongamos que observamos los vectores nulos: la condición $\det V = 0$ fuerzas $V$ ser una proyección, en otras palabras, $$V = \begin{bmatrix}\alpha \\ \beta \end{bmatrix}\begin{bmatrix}\alpha^* & \beta^* \end{bmatrix} = \begin{bmatrix}\alpha^* ~\alpha & \alpha ~\beta^* \\ \alpha^*~ \beta & \beta ~\beta^*\end{bmatrix}$$ En particular, para los vectores de futuro nulos $r^\mu = (r, \vec r)$ podemos interpretar $(v^1 + i v^2) / (v^0 - v^3)= \alpha^* \beta / (\beta^* \beta) = (\alpha/\beta)^*$ como el proyección estereográfica de $\vec r$ en $\mathbb C.$ Así que no estamos en el país de la laya; esta es una forma real de hablar de hacia dónde va la luz. En particular, el punto complejo $\alpha/\beta = 0$ es la proyección del punto $(x, y, z) = (0, 0, -r)$ mientras que la proyección del punto $(0, 0, +r)$ es complejo $\infty$ .

Ahora acabamos de escribir nuestro $\det V = 0$ matriz $V$ en la forma $v ~ v^\dagger$ donde $v = [\alpha;\;\beta];$ este objeto es el llamado espinor que representa el vector nulo. La acción del impulso $V \mapsto L V L^\dagger$ es el mismo que el efecto $v \mapsto L v$ . A su vez, esta cantidad $\gamma = \alpha / \beta$ que nos dice hacia dónde se dirige el rayo de luz (en coordenadas estereográficas) es mapeado por la matriz de Lorentz $\begin{bmatrix} a&b\\c&d\end{bmatrix}$ al nuevo valor $\gamma' = (a~\alpha + b~\beta)/(c~\alpha + d~\beta).$

Para la anterior matriz de refuerzo de Lorentz el resultado que se obtiene es $\gamma' = e^w ~ \gamma.$

Así pues, imaginemos una densidad esférica uniforme de vectores nulos salientes de una esfera estacionaria. Imaginemos que son puntos en el plano complejo. Nos impulsamos en un marco donde esa esfera va hacia $+z$ con velocidad $c \tanh w$ . Todos los puntos se mueven desde algún $\gamma$ a algún nuevo $e^w~\gamma$ , siendo "escalados" hacia fuera en magnitud. Esto equivale a que se alejen homogéneamente de $z = -r$ y hacia $z = +r$ que es en la dirección del movimiento.

Eso es un rayo relativista. La luz, que parece localmente isotrópica, se "transmite" en la misma dirección en la que se mueve la partícula a través del impulso de Lorentz.