En primer lugar, hay un gran estudio de los espacios topológicos localmente convexos en la sección 424 del Diccionario Enciclopédico de Matemáticas. (El EDM, si no lo has visto, es una referencia fabulosa para todo tipo de información. Aunque todos tengamos la Wikipedia, el EDM sigue siendo genial). Al final tiene un gráfico de muchas de estas propiedades de los espacios vectoriales topológicos, indicando las dependencias, aunque no todas. Este gráfico me ayudó mucho con tu pregunta. En ese sentido, No soy un analista funcional, pero puedo jugar uno en MO . Tal vez un analista funcional serio pueda darle una respuesta mejor. (¿O una respuesta peor? Me pregunto si para algunos analistas todo es la máquina).
Todos los espacios vectoriales topológicos importantes que he visto en matemáticas (de los que son más $\mathbb{R}$ o $\mathbb{C}$ ) es al menos un Espacio de Banach o una importante generalización conocida como Espacio de Frechet o se deriva de uno de los dos. Todos hemos aprendido lo que es un espacio de Banach; un espacio de Frechet es lo mismo, pero con una familia contable de seminormas en lugar de una norma. Muchas de las propiedades que enumeras, por ejemplo la metrizabilidad y la bornología, se dan en todos los espacios de Frechet. Al enfatizar los espacios de Banach y Frechet, la propiedad de completitud es implícitamente importante. Dado que un espacio lineal normado es un espacio métrico, también se puede tomar su compleción, lo que lo convierte en Banach. Un espacio de Frechet es una generalización de un espacio métrico conocido como espacio uniforme y tú también podrías hacer lo mismo. Además, la discusión no está completa sin mencionar los espacios de Hilbert. Se puede pensar en un Espacio de Hilbert ya sea como una construcción de un tipo de espacio de Banach, o un espacio de Banach que satisface la ley del paralelogramo; por supuesto que es importante.
De las propiedades que no se mantienen para todos los espacios de Frechet, se me ocurren cuatro que realmente importan: reflexiva, nuclear, separable e incondicional. Además, un espacio de Schwartz no es realmente un espacio con una propiedad, sino una construcción específica (y útil) de un espacio de Frechet. ( Editar: Parece que "Schwartz" significa dos cosas, el espacio de Schwartz de las funciones suaves rápidamente decrecientes, y la propiedad de Schwartz de un espacio localmente convexo).
Una discusión de las propiedades que creo que vale la pena conocer, y por qué:
-
reflexivo . Esto significa un espacio cuyo dual es también su predual. Si un espacio de Banach tiene un predual, entonces su bola unitaria es compacta en la topología débil-* por el teorema de Banach-Alaoglu. En particular, el conjunto de medidas de probabilidad de Borel en un espacio compacto es compacto. Esto es importante en geometría, sin duda. Como es sabido, los espacios de Hilbert son reflexivos. Obsérvese también que hay una segunda topología importante, la topología débil-* cuando existe un pre-dual, que también se llamaría topología débil en el caso reflexivo. (No estoy seguro de qué sirve la topología débil cuando son diferentes).
-
separable . Como en topología, tiene un subconjunto denso contable. ¿Cuánto se utilizan los colectores que no tienen un subconjunto denso contable? Los vectores topológicos inseparables tampoco suelen ser tan útiles, con la principal excepción del dual de un espacio de Banach no reflexivo y separable. Por ejemplo $B(H)$ , los operadores acotados sobre un espacio de Hilbert, es inseparable, pero es el dual del espacio de Banach de los operadores de clase traza $B_1(H)$ que es separable.
-
incondicional . Es bueno que un espacio de Banach tenga una base, y el tipo razonable es una base topológica, también conocida como base de Schauder. La estructura no se parece tanto al álgebra lineal familiar si las combinaciones lineales sólo son condicionalmente convergentes. Una base incondicional es una base topológica no ordenada, y un espacio incondicional es un espacio de Banach que tiene una. Hay un maravilloso teorema de estructura que dice que, hasta un factor constante que puede ser enviado a 1, la norma en un espacio incondicional es una función convexa de las normas de las coordenadas de la base. Todos los espacios de Banach incondicionales se parecen a $\ell^p$ en este sentido. Nótese también que existe una generalización moral no conmutativa para los operadores, a saber, que la norma sea espectral o invariante bajo el grupo unitario disponible.
-
nuclear . Muchas de las propiedades favorables de las funciones suaves $C^\infty(M)$ en una variedad compacta provienen o están relacionadas con el hecho de que es un espacio nuclear de Frechet. Por ejemplo, al definirlo como un espacio de Frechet (utilizando normas sobre las derivadas), se observa que las normas precisas no importan mucho. Esto no significa necesariamente que deba aprender la teoría de los espacios nucleares (ya que incluso la mayoría de los analistas no lo hacen). Pero al trazar una línea entre las construcciones y las propiedades, La opinión parece estar dividida en cuanto a si la teoría de los espacios nucleares es tangencial o fundamental. En cualquier caso, mi impresión es que las principales propiedades favorables de $C^\infty(M)$ son que es Frechet, reflexivo y nuclear. Por otro lado, los espacios de Banach de dimensión infinita nunca son nucleares.
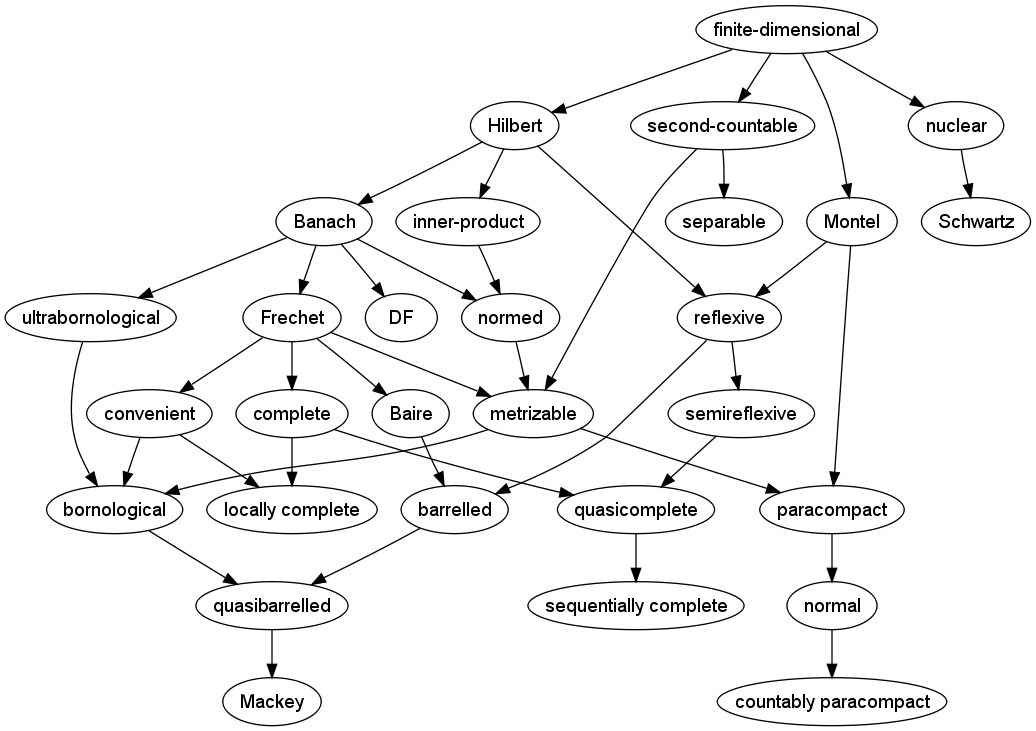
A raíz de la pregunta de Andrew, he recopilado algunos datos sobre las relaciones entre los tipos de espacios topológicos localmente convexos. En particular, hice un diagrama de Hasse (dibujado con Graphviz ) de las propiedades incluidas a continuación. Comenzó como una simplificación de la de EDM, pero luego añadí más condiciones. La regla para el diagrama de Hasse es que sólo permito propiedades de "un solo nombre", no cosas como Frechet y nuclear, aunque los adverbios están permitidos. El gráfico hace que el tema de los espacios localmente convexos parezca ridículamente complicado, pero eso es un poco injusto. Se podría argumentar que hay más que suficientes propiedades definidas en el campo, pero por supuesto los matemáticos siempre tienen derecho a hacer nuevas preguntas. Además, si te fijas bien, relativamente pocas propiedades de la parte superior del diagrama implican la mayoría de las demás, lo cual es parte del objetivo de mi respuesta. Si un espacio vectorial topológico es de Banach o incluso de Frechet, entonces automáticamente tiene una docena de otras propiedades enumeradas.
Tengo la sensación de que en el diagrama de Hasse faltan aristas incluso para los nodos que aparecen. Si alguien quiere añadir comentarios al respecto, sería estupendo. (O podría ser una futura pregunta de MO.) La pregunta más difícil es la de las combinaciones de propiedades. Preveo una encuesta asistida por ordenador para comparar todas las posibles combinaciones de propiedades importantes, junto con citas de contraejemplos y estado abierto, según corresponda. Hace unos años comencé un estudio similar de clases de complejidad asistido por ordenador.
![Diagram of some LCTVS properties]()