En el instante en que un objeto acelerado tiene velocidad cero, ¿se está acelerando, desacelerando o ninguna de las dos?

Question

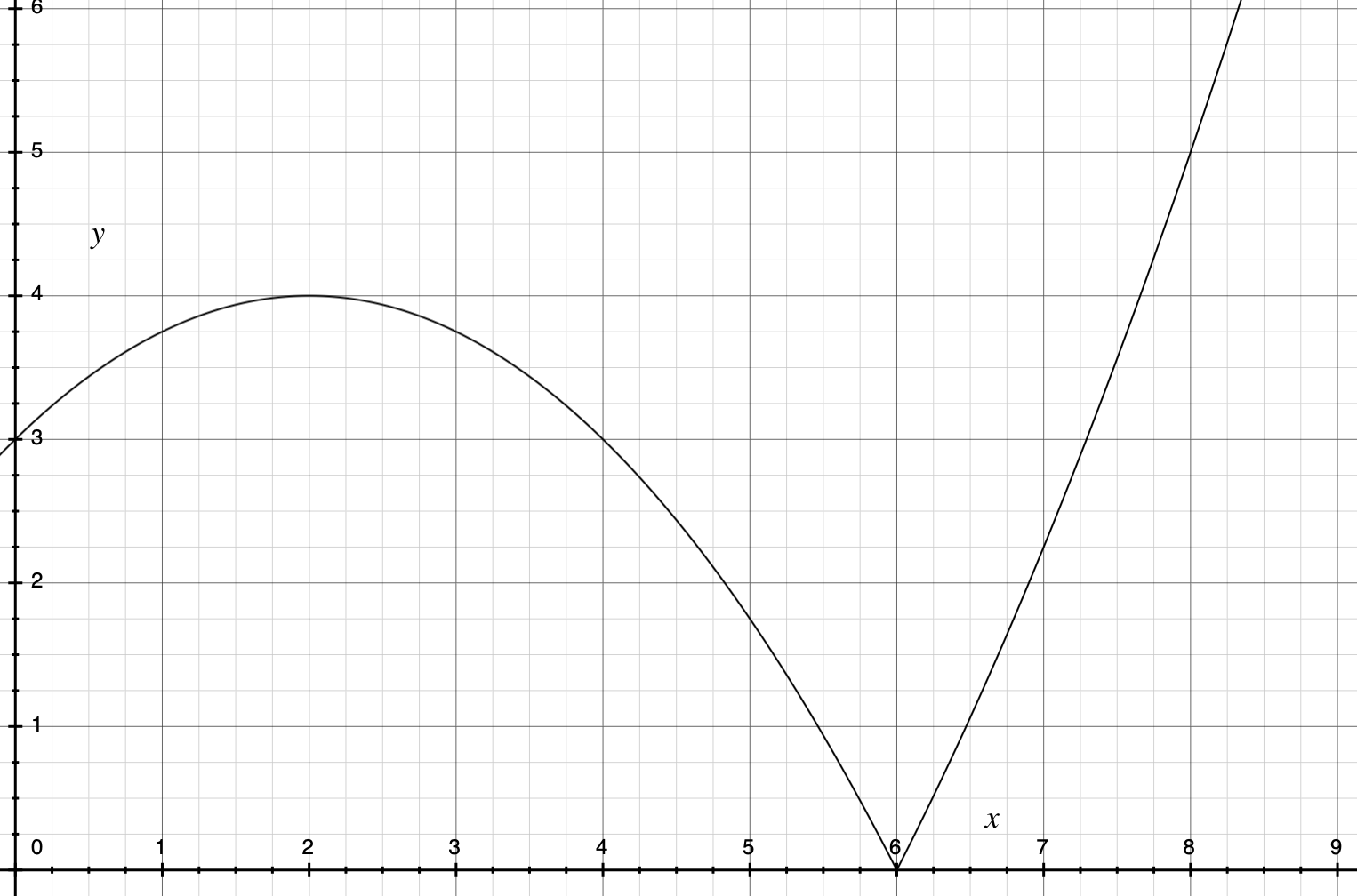
Este problema es de Khan Academy. Específicamente para el punto azul marcado en rojo, la respuesta es que en este punto azul, el objeto ni está acelerando ni desacelerando. Cuando pienso en la regla sobre los signos de la velocidad y la aceleración y lo que esto significa para el cambio en la velocidad, tiene sentido: si la velocidad y la aceleración tienen el mismo signo, el objeto está acelerando, y si la velocidad y la aceleración tienen signos opuestos, el objeto está desacelerando. En el punto azul, la velocidad instantánea es cero y como el cero no es ni positivo ni negativo, el objeto ni está acelerando ni desacelerando.

Sin embargo, intuitivamente, esto no tiene sentido. En el punto azul marcado en rojo, la velocidad es cero, por lo que la velocidad debe ser cero. Además, la pendiente de la función en este punto azul es negativa, por lo que la aceleración es negativa, lo que significa que la velocidad está disminuyendo cada segundo. Si la velocidad está disminuyendo cada segundo, entonces justo después de 6 segundos, la velocidad se volverá negativa pero la velocidad habrá aumentado. Entonces, en el punto azul, el objeto, aunque tiene velocidad cero, está en el proceso de acelerar. ¿Por qué este pensamiento es incorrecto?

Answer 1

La parte complicada de esta pregunta es que se te da un gráfico de velocidad pero se te hace una pregunta sobre la velocidad.

Varios otros han dicho prácticamente lo mismo, pero lo que realmente me hace entender esto es un gráfico de velocidad:

Lo anterior es el gráfico de $$ y = \left \lvert 4 - \left ( \frac{x - 2}{2} \right ) ^2 \right \rvert \text{,}$$ que es simplemente el valor absoluto del gráfico de velocidad en tu captura de pantalla.

Esto representa el hecho de que la velocidad es el valor absoluto de la velocidad.

Entendemos "reducción de velocidad" como que la pendiente de la velocidad es negativa, y "aumento de velocidad" como que la pendiente de la velocidad es positiva. ¿Cuál es la pendiente del punto $(6, 0)$ en el gráfico (que corresponde al punto circular)?

Este punto es una cúspide. La noción de "pendiente" sólo existe para puntos diferenciables, y como dice Wikipedia,

una función con una curva, cúspide o tangente vertical puede ser continua, pero no es diferenciable en la ubicación de la anomalía.

Por lo tanto, la pendiente de la velocidad no existe en este punto, y por lo tanto el objeto ni está aumentando ni disminuyendo su velocidad en este instante.

Answer 2

Proporcionaré una respuesta un poco más formal. "Acelerar" o "desacelerar" típicamente se refiere a si la velocidad de un objeto está aumentando o disminuyendo. Imagina que estás en un bote acelerando por un canal (de manera que solo puedas moverte en una dimensión - el canal es muy estrecho). En $t=2$, cambias un interruptor y tu motor comienza a funcionar en reversa. Aquí hay un instante donde tu aceleración es 0 antes de volverse negativa, y esto corresponde al máximo en tu gráfica de velocidad-tiempo. Ahora, tu motor está funcionando en reversa y tu bote está "desacelerando" en el sentido tradicional. Esto corresponde a $2 en tu gráfica. Llega un instante donde has eliminado toda tu velocidad, y comienzas a funcionar en reversa. Después de eliminar tu velocidad, tu velocidad comienza a aumentar (estás "acelerando").

En matemáticas, podemos explicarlo de la siguiente manera. La velocidad de un objeto se define como la magnitud de su velocidad. En 1 dimensión, esto significa

$$ s = |v| $$ es decir, la velocidad es el valor absoluto de la velocidad. Si estamos interesados en si estás acelerando o desacelerando, queremos encontrar $ds/dt$. Esto se puede hacer usando la regla de la cadena del cálculo ordinario. Primero, notamos que: $$ |v| \equiv \sqrt{v^2} = (v^2)^{1/2} $$ como definición. Ahora tomamos la derivada: $$ \begin{align} \frac{d|v|}{dt} &= \frac{d(v^2)^{1/2}}{dt}\\ &=\frac{1}{2}(v^2)^{-1/2}\cdot 2v\cdot \frac{dv}{dt} \\ &= \frac{v}{\sqrt{v^2}}\cdot \frac{dv}{dt} \\ &=\frac{v}{\sqrt{v^2}}\cdot a \end{align} $$

Esta expresión final nos dice varias cosas. Primero, recuperamos la regla con la que estás familiarizado: es decir, si $v$ y $a$ tienen el mismo signo, entonces $ds/dt$ será positivo. Si tienen signos opuestos, será negativo. Sin embargo, también notamos que tenemos una discontinuidad en $v=0$, que es la situación considerada aquí. En cero, $v/\sqrt{v^2}$ salta de $-1$ a $1$ y la derivada $ds/dt$ no existe - la velocidad es formalmente indefinida. Esto se conoce como la función signo $sgn(v)$, que devuelve el signo del argumento. Dado que la derivada de la velocidad no existe en $v=0$ en una dimensión, estamos justificados en decir que ni aceleras ni desaceleras. Sin embargo, la velocidad está disminuyendo todo este tiempo, como se evidencia por la constante aceleración negativa.

Answer 3

En el primer punto antes del que has marcado, el objeto se está desacelerando. Su velocidad instantánea está disminuyendo y acercándose al eje cero. Sin embargo, en $0 \, \frac{m}{s}$, la velocidad instantánea ha dejado de disminuir (porque ahora ha llegado a cero, no puede desacelerar más que $0\, \frac{m}{s}$) pero aún no ha comenzado a acelerar en la dirección negativa.

Puede que te preguntes, "¿cómo puede no estar acelerando o desacelerando si su aceleración no es cero?" Como sabemos, la aceleración es la pendiente de la gráfica. En el punto marcado la aceleración es distinta de cero porque el objeto está cambiando de dirección de la positiva a la negativa, no porque esté acelerando/desacelerando.

Los signos positivos y negativos aquí no se refieren a desaceleración y aceleración; se refieren a dos direcciones - la dirección positiva y negativa. Si esto fuera un gráfico de posición vs. tiempo, entonces negativo se referiría a una posicion negativa con respecto a la posición cero y viceversa para la posición positiva. Los signos positivos y negativos se utilizan aquí para darte una línea unidimensional a lo largo de la cual puedes moverte en dos direcciones con el origen siendo un punto arbitrario que llamamos cero.

Una buena analogía física unidimensional para esta pregunta (aunque su curva de velocidad sería lineal y no curva) es una pelota que cae verticalmente. Después de impactar con el suelo se mueve $0 \,\frac{m}{s}$ y ha perdido toda su velocidad descendente pero aún no ha ganado ninguna velocidad ascendente en ese instante (está en la "etapa intermedia entre acelerar y desacelerar"). La explicación matemática para esto es que la derivada de la magnitud de $v$ (que determina si el objeto está acelerando/desacelerando) es indefinida. En ese instante la aceleración (la derivada de $v$, no la magnitud de $v$) es distinta de cero y apuntando hacia arriba, actuando para cambiar la dirección de movimiento de la pelota.

Answer 4

Algo no parece correcto. Para una curva de velocidad versus tiempo, la aceleración en cualquier punto de la curva es la derivada de la función, es decir, la pendiente instantánea de la curva en ese punto.

En el punto marcado el la pendiente es negativa y no cero, lo que indica una aceleración negativa. Así que mientras la velocidad en el punto marcado es cero, todavía está cambiando, en este caso cambio de dirección.

Por otro lado, la pendiente de la curva correspondiente a t=2 segundos parece ser cero. Ahí es donde la aceleración es cero.

Espero que esto ayude.

Answer 5

La velocidad es la magnitud de la velocidad y, por lo tanto, siempre es una cantidad positiva.

Si los términos "acelerar" y "desacelerar" se refieren a la velocidad, entonces en el momento indicado en el gráfico la velocidad es cero y, después de haber alcanzado un mínimo (cero), la velocidad habría estado aumentando en el futuro.
El problema es que antes de ese momento la velocidad estaba disminuyendo para eventualmente llegar a cero y eso significa que un gráfico de velocidad contra tiempo es discontinuo en el momento en cuestión, es decir, la pendiente del gráfico no está definida en ese momento.
Entonces, ¿quizás por eso se dio la respuesta "ninguno" como correcta?

La tasa de cambio de velocidad (aceleración), la pendiente del gráfico de velocidad contra tiempo que está bien definida, es negativa y por lo tanto, en ese momento la tasa de cambio de velocidad (aceleración) es negativa.
Lo que estaba sucediendo era que la dirección del movimiento del cuerpo cambió en ese momento, pasando de moverse en dirección positiva a moverse en dirección negativa.
Entonces se podría decir que el componente de velocidad, en la dirección que se eligió como positiva, pasó de ser positivo a ser negativo.
La etiqueta en el gráfico "velocidad" es una abreviatura de "componente de velocidad en una dirección elegida".

Si alguien mirara el velocímetro (un dispositivo que mide la velocidad) justo antes de que la velocidad estuviera disminuyendo y justo después de ese momento la velocidad estuviera aumentando, pero en el instante de tiempo en cuestión, ¿cuál de las dos opciones elegirías?