Tenga en cuenta que el test de Shapiro-Wilk es una prueba poderosa de normalidad.
El mejor enfoque es realmente tener una buena idea de la sensibilidad de cualquier procedimiento que desee utilizar a diversos tipos de no-normalidad (¿qué tan no normal debe ser de esa manera para afectar su inferencia más de lo que puede aceptar?).
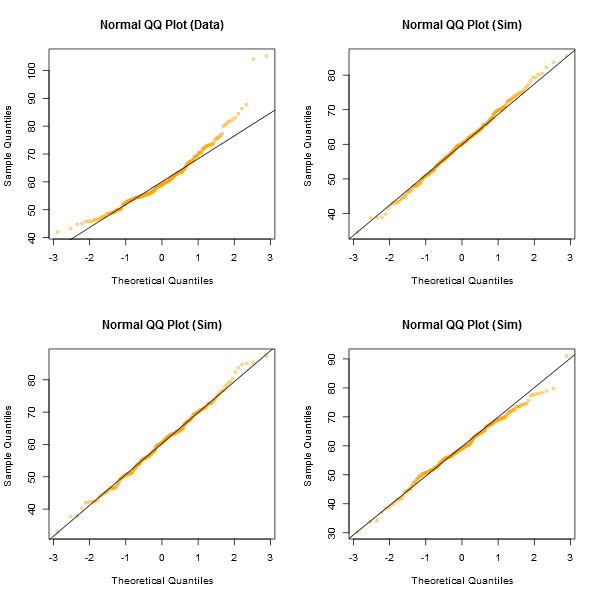
Un enfoque informal para observar los gráficos sería generar una serie de conjuntos de datos que sean realmente normales del mismo tamaño de muestra que el que tiene, por ejemplo, 24 de ellos. Grafique sus datos reales entre una cuadrícula de esos gráficos (5x5 en el caso de 24 conjuntos aleatorios). Si no se ve especialmente inusual (el peor aspecto, digamos), está razonablemente consistente con la normalidad.
![introducir descripción de la imagen aquí]()
A mi parecer, el conjunto de datos "Z" en el centro se ve aproximadamente igual que "o" y "v" y quizás incluso "h", mientras que "d" y "f" se ven ligeramente peor. "Z" son los datos reales. Aunque no creo ni por un momento que sean realmente normales, no llaman especialmente la atención cuando se comparan con datos normales.
[Editar: acabo de realizar una encuesta aleatoria ---bueno, le pregunté a mi hija, pero en un momento bastante aleatorio-- y su elección para el menos parecido a una línea recta fue "d". Así que el 100% de los encuestados consideró que "d" era el más extraño.]
Un enfoque más formal sería realizar una prueba de Shapiro-Francia (que se basa efectivamente en la correlación en la gráfica QQ), pero (a) ni siquiera es tan potente como la prueba de Shapiro-Wilk, y (b) las pruebas formales responden a una pregunta (a veces) que ya deberías conocer de antemano (la distribución de la cual se extrajeron tus datos no es exactamente normal), en lugar de la pregunta que necesitas responder (¿cuánto importa eso?).
Como se solicitó, aquí está el código para la visualización anterior. Nada complicado involucrado:
z = lm(dist~speed,cars)$residual
n = length(z)
xz = cbind(matrix(rnorm(12*n), nr=n), z,
matrix(rnorm(12*n), nr=n))
colnames(xz) = c(letters[1:12],"Z",letters[13:24])
opar = par()
par(mfrow=c(5,5));
par(mar=c(0.5,0.5,0.5,0.5))
par(oma=c(1,1,1,1));
ytpos = (apply(xz,2,min)+3*apply(xz,2,max))/4
cn = colnames(xz)
for(i in 1:25) {
qqnorm(xz[, i], axes=FALSE, ylab= colnames(xz)[i],
xlab="", main="")
qqline(xz[,i],col=2,lty=2)
box("figure", col="darkgreen")
text(-1.5,ytpos[i],cn[i])
}
par(opar)
Tenga en cuenta que esto fue solo con fines de ilustración; quería un pequeño conjunto de datos que pareciera ligeramente no normal, por lo que utilicé los residuos de una regresión lineal en los datos de autos (el modelo no es del todo apropiado). Sin embargo, si realmente estuviera generando tal visualización para un conjunto de residuos para una regresión, regresaría los 25 conjuntos de datos en las mismas $x$'s que en el modelo, y mostraría gráficos QQ de sus residuos, ya que los residuos tienen cierta estructura no presente en números aleatorios normales.
(He estado realizando conjuntos de gráficos como este desde mediados de los años 80 al menos. ¿Cómo puedes interpretar gráficos si no estás familiarizado con cómo se comportan cuando se cumplen las suposiciones --- y cuando no?)
Ver más:
Buja, A., Cook, D. Hofmann, H., Lawrence, M. Lee, E.-K., Swayne, D.F and Wickham, H. (2009) Statistical Inference for exploratory data analysis and model diagnostics Phil. Trans. R. Soc. A 2009 367, 4361-4383 doi: 10.1098/rsta.2009.0120
Editar: Mencioné este tema en mi segundo párrafo pero quiero enfatizar el punto nuevamente, en caso de que se olvide en el camino. Lo que generalmente importa no es si puedes notar que algo no es realmente normal (ya sea mediante prueba formal o mirando un gráfico) sino más bien cuánto importa para lo que usarías ese modelo: ¿Qué tan sensibles son las propiedades que te importan a la cantidad y manera de la falta de ajuste que podrías tener entre tu modelo y la población real?
La respuesta a la pregunta "¿la población de la que estoy muestreando está realmente distribuida normalmente" es, esencialmente siempre, "no" (no necesitas una prueba o un gráfico para eso), pero la pregunta es más bien "¿cuánto importa?". Si la respuesta es "poco o nada", el hecho de que la suposición sea falsa tiene poca consecuencia práctica. Un gráfico puede ayudar en cierta medida ya que al menos te muestra algo de la 'cantidad y manera' de desviación entre la muestra y el modelo de distribución, por lo que es un punto de partida para considerar si importaría. Sin embargo, si importa depende de las propiedades de lo que estás haciendo (considera una prueba t versus una prueba de varianza, por ejemplo; la prueba t en general puede tolerar desviaciones mucho más sustanciales de las suposiciones que se hacen en su derivación que una prueba de la relación F de igualdad de varianzas).
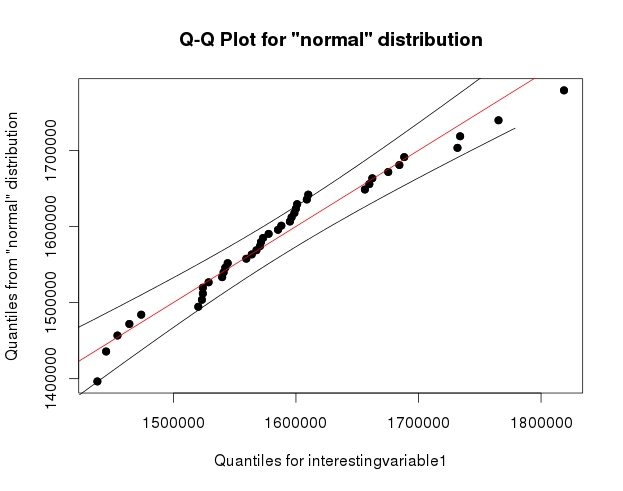
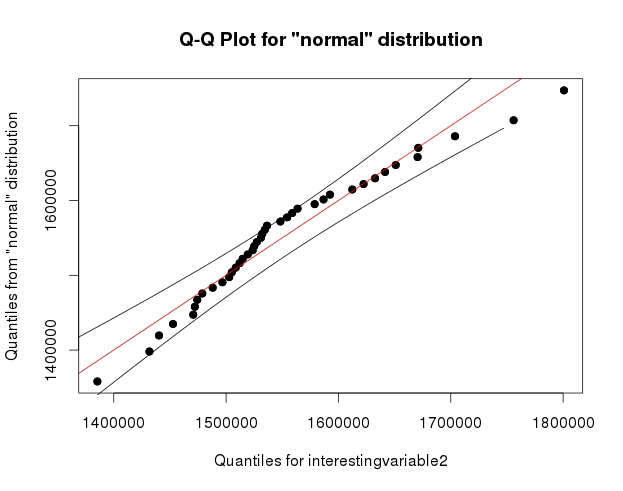


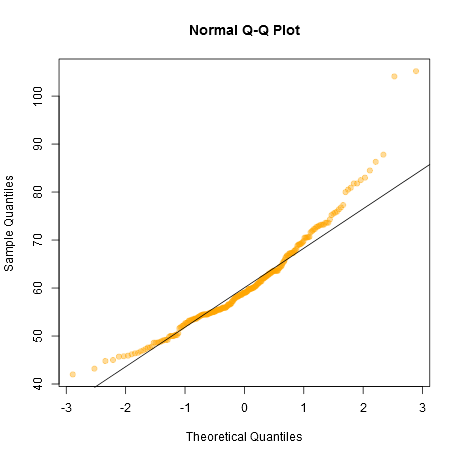
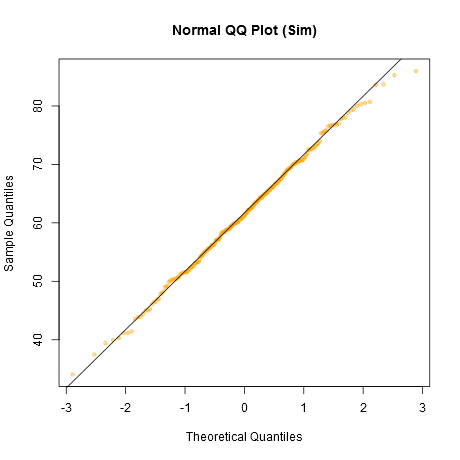


3 votos
Las bandas de confianza alrededor de la línea QQ son bastante geniales. ¿Puedes compartir el código R que usaste para obtenerlas?
8 votos
Es solo qqPlot() de {qualityTools} :)