Sobre la suma de variables aleatorias independientes uniformes

Question

Dejemos que $X_1,...,X_n$ sean variables aleatorias uniformes e independientes en [0,1] y supongamos $c>1/2$ . ¿Es cierto que $$\mathbb{P}\left[\sum_{i=1}^n X_i \leq n \cdot c\right]$$ es creciente con respecto a $n$ ?

Sé que la suma de aleatorias independientes uniformes sigue la distribución Irwin-Hall, pero parece difícil trabajar con la pdf. ¿Tal vez un argumento de acoplamiento? Quiero destacar que queremos mostrar el resultado para todos $n$ no sólo para $n$ suficientemente grande.

Answer 1

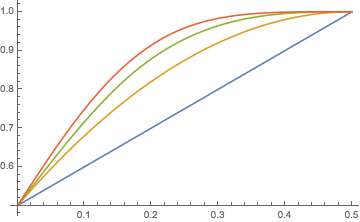
La respuesta es sí. Deje que $S_n:=\sum_{i=1}^n X_i$ , $x\in\mathbb R$ , $n=2,3,\dots$ y \begin{equation} G_n(x):=P(S_n/n\le x)=\frac1{n!}\,\sum_j(-1)^j\binom nj (nx-j)_+^n, \end{equation} donde $u_+:=0\vee u$ ; cf. [ Distribución de Irwin--Hall ] . La suma aquí es sobre todos los enteros $j$ con la convención habitual de que $\binom nj=0$ si $j\notin\{0,\dots,n\}$ . Sea \begin{equation} D_n(x):=G_{n+1}(x)-G_n(x). \end{equation} Tenemos que demostrar que $D_n(x)\ge0$ para $x\ge1/2$ .

Claramente, $D_n$ es $n-1$ veces continuamente diferenciable, $D_n=0$ en el exterior $(0,1)$ y $D_n(1-x)=-D_n(x)$ (simetría). Para las pequeñas $x>0$ , uno tiene $G_n(x)=\frac1{n!}\,n^nx^n>\frac1{(n+1)!}\,(n+1)^{n+1}x^{n+1}=G_{n+1}(x)$ De ahí que $D_n(x)<0$ De ahí que $D_n>0$ en una vecindad izquierda de $1$ con $D_n(1)=0$ . También, $D_n(1/2)=0$ . Por lo tanto, basta con demostrar que $D_n$ no tiene raíces en $(1/2,1)$ .

Supongamos lo contrario. Entonces, por la simetría, $D_n$ tiene al menos $3$ raíces en $(0,1)$ . Entonces, por el teorema de Rolle, la derivada $G_n^{(n-1)}$ de $G_n$ de orden $n-1$ tiene al menos $3+n-1=n+2$ raíces en $(0,1)$ . Esto contradice el hecho (demostrado más adelante) de que, para cada número entero $j$ tal que $n-1\ge j\ge\frac{n-1}2$ , $D_n$ tiene exactamente una raíz en el intervalo $$h_{n,j}:=[\tfrac jn,\tfrac{j+1}n).$$

De hecho, tome cualquier $x\in[1/2,1]$ . No es difícil ver que, para $j_x:=j_{n,x}:=\lfloor nx\rfloor$ , \begin{equation} G_n^{(n-1)}(x)=n^{n-1}\sum_{j=0}^{j_x}(-1)^j\binom nj (nx-j) \end{equation}
\begin{equation} =\frac{n^{n-1}}{n-1}(-1)^{j_x}\binom n{j_x+1}({j_x}+1) ((n-1)x-{j_x}). \end{equation} Del mismo modo, para $k_x:=j_{n+1,x}$ , \begin{equation} G_{n+1}^{(n-1)}(x)=\frac{(n+1)^{n-1}}{2n(n-1)} (-1)^{k_x}\binom{n+1}{k_x+1}(k_x+1)P(n,k_x,x), \end{equation} donde \begin{equation} P(n,k,x):=-2 k \left(n^2-1\right) x+k (k n-1)+n \left(n^2-1\right) x^2. \end{equation} Tenga en cuenta que $k_x\in\{j_x,j_x+1\}$ . Ahora tenemos que considerar los dos casos siguientes.

Caso 1: $k_x=j_x=j\in[\frac{n-1}2,n-1]$ lo que equivale a $x\in h'_{n,j}:=[\frac jn,\frac{j+1}{n+1})$ . También se deduce que en este caso $j\ge n/2$ . En este caso, no es difícil comprobar que $D_n(x)$ es igual a $(-1)^j P_{n,j,1}(x)$ en signo, donde \begin{equation} P_{n,j,1}(x):=2 j n^n (n-j)+x \left(-2 (n-1) n^n (n-j)-2 j (n+1)^n \left(n^2-1\right)\right)+j (n+1)^n (j n-1)+(n+1)^n \left(n^2-1\right) n x^2, \end{equation} que es convexo en $x$ . Además, $P_{n,j,1}(\frac jn)$ y $P_{n,j,1}(\frac{j+1}{n+1})$ cada uno es igual a $2 n^n - (1 + n)^n<0$ en señal. Así que, $P_{n,j,1}<0$ y por lo tanto $D_n$ no tiene raíces en $h''_{n,j}=[\frac jn,\frac{j+1}{n+1})$ .

Caso 2: $k_x=j+1$ y $j_x=j\in[\frac{n-1}2,n-1]$ lo que equivale a $x\in h''_{n,j}:=[\frac{j+1}{n+1},\frac{j+1}n)$ . En este caso, no es difícil comprobar que $D_n(x)$ es igual a $(-1)^{j+1} P_{n,j,2}(x)$ en signo, donde \begin{equation} P_{n,j,2}(x):=(j+1) \left((n+1)^n (j n+n-1)-2 j n^n\right)+2 (j+1) \left((n-1) n^n-(n+1)^n \left(n^2-1\right)\right) x+n \left(n^2-1\right) (n+1)^n x^2, \end{equation} que es convexo en $x$ . Además, $P_{n,j,1}(\frac{j+1}n)$ y $-P_{n,j,1}(\frac{j+1}{n+1})$ cada uno es igual a $2 n^n - (1 + n)^n<0$ en señal. Así que, $P_{n,j,2}$ tiene exactamente una raíz en $h''_{n,j}$ y por lo tanto también lo hace $D_n$ .

Dado que el intervalo $h_{n,j}$ es la unión disjunta de $h'_{n,j}$ y $h''_{n,j}$ , $D_n$ tiene exactamente una raíz en $h_{n,j}=[\tfrac jn,\tfrac{j+1}n)$ y la prueba está completa.

Answer 2

Vamos a escribir $p_n(x)=P(S_n\le nx)$ queremos demostrar que esto aumenta en $n$ por el hecho de ser fijo $x>1/2$ . Al condicionar a $X_{n+1}$ obtenemos que $$ p_{n+1}(x) = \int_0^1 p_n\left( x+ \frac{x-y}{n} \right) \, dy = n\int_{x-(1-x)/n}^{x+x/n} p_n(t)\, dt . $$ Así que nos preguntamos si $$ p_n(x) \le n \int_{x-(1-x)/n}^{x+x/n} p_n(t)\, dt \quad\quad\quad\quad (1) $$ Por una expansión de Taylor, el lado derecho de (1) es igual a $$ p_n(x) + p_n'(x) \frac{2x-1}{2n} + O(p_n''/n^2) , $$ así que habríamos terminado si pudiéramos establecer que $|p_n''(t)|\lesssim n p_n'(x)$ cerca de $t=x$ con una constante implícita suficientemente pequeña. Si volvemos a la distribución de Irwin Hall $F_n(a)=P(S_n\le a)$ , entonces esto se convierte en $|F_n''(t)|\lesssim F_n'(nx)$ cerca de $t=nx$ y al menos para los grandes $n$ Esto es cierto ya que $F''_n$ no varía mucho en un intervalo de longitud $L$ por lo que no puede ser mucho mayor que $F'_n(x)/L$ .

Comentario: Si volvemos a (1), vemos que hay efectos contrapuestos. Por un lado, estamos promediando sobre un intervalo asimétrico, dando preferencia a los puntos $t>x$ donde $p_n(t)>p_n(x)$ , lo cual es bueno. Por otro lado, $p_n''<0$ lo cual es malo, porque esto significa que $p_n$ disminuye más rápidamente yendo hacia la izquierda de $x$ de lo que aumenta yendo hacia la derecha.

Answer 3

Déjame escribir $c=1/2+\delta$ y definir $$P_n(\delta)\equiv \mathbb{P}\left[\sum_{i=1}^n X_i \leq n \cdot c\right].$$ Tenga en cuenta que $P_n(0)=1/2$ y $P_n(1/2)=1$ independientemente de $n$ .

Es conveniente trabajar con la función característica del Distribución de Irwin-Hall . Encuentro la integral del valor principal $$\mathbb{P}\left[\sum_{i=1}^n X_i \leq n \cdot c\right]=\frac{1}{2}-\frac{1}{2\pi}\int_{-\infty}^\infty dt\,\frac{1}{(it)^{n+1}}\left(e^{it(1-c)}-e^{-ict}\right)^n,$$ que se puede reescribir como $$P_n(\delta)=\frac{1}{2}+\frac{1}{\pi}\int_{0}^\infty dt\,\sin(2nt\delta)\,\frac{\sin^n t}{t^{n+1}}.$$

El gráfico muestra $P_n(\delta)$ para $n=1,2,3,4$ de la curva inferior a la superior. Tenemos que demostrar que esta ordenación de $P_n(\delta)$ con el aumento de $n$ es válida para todos los $n$ Así que $P_n(\delta)$ aumenta con $n$ para todos $\delta\in(0,1/2)$ . Intentaré demostrarlo en varios pasos.

(I) $P_n(\delta)$ aumenta con $n$ cerca de $\delta=0$ .

Para los pequeños $\delta$ la integral se evalúa como

$$P_n(\delta)=\tfrac{1}{2}+2nC_n\delta+{\cal O}(\delta^3),$$

con el coeficiente

$$C_n=\frac{1}{\pi}\int_0^\infty dt\,\frac{\sin^n t}{t^n}.$$

Esta integral sobre el $n$ -la potencia de la función sinc es bien estudiado necesitamos demostrar que disminuye más lentamente que $1/n$ . Para los pequeños $n$ esto se puede comprobar mediante un cálculo explícito, para grandes $n$ se deduce del decaimiento asintótico $C_n\propto 1/\sqrt n$ . Así que la pendiente $P'_n(0)=2nC_n\propto \sqrt n$ es efectivamente una función creciente de $n$ .

(II) $P_n(\delta)$ aumenta con $n$ cerca de $\delta=1/2$ .

Esto se desprende de una expansión similar en torno a $\delta=1/2$ , lo que demuestra que el primer no-cero $p$ -derivada de orden $P_n^{(p)}(1/2)$ se produce para $p=n$ . Tan cerca $\delta=1/2$ la función se expande como

$$P_n(\delta)=1-(-1)^n A_n(\delta-1/2)^n+{\cal O}(\delta-1/2)^{n+1},\;\;A_n>0,$$

por lo que $P_n(\delta)$ aumenta con $n$ para $\delta$ justo debajo $1/2$ .

(III) Grande $n$ asintótica

Para $n\gg 1$ la integral sinc puede evaluarse en forma cerrada mediante el límite $$\lim_{n\rightarrow\infty}\left(\frac{\sin(t/\sqrt n)}{t/\sqrt n}\right)^n=\exp(-t^2/6)$$ para que $P_n(\delta)$ se convierte asintóticamente en $$P_n(\delta)\rightarrow\frac{1}{2}+\frac{1}{\pi}\int_0^\infty dt\,\sin(2t\delta\sqrt n)\frac{1}{t}\exp(-t^2/6)=\frac{1}{2}+\frac{1}{2}\,{\rm Erf}\,(\delta\sqrt{6n}),$$ que efectivamente tiene un incremento monotónico $n$ -para cada uno de ellos. $\delta\in(0,1/2)$ .

Obsérvese que recuperamos el $\sqrt n$ pendiente en $\delta=0$ , $$P'_n(0)\rightarrow \sqrt{6n/\pi}\;\;\text{for}\;\;n\rightarrow\infty.$$ En $\delta=1$ la desviación del límite exacto $P_n(1/2)=1$ es exponencialmente pequeño, $\propto\exp(-3n/2)/\sqrt n$ .

La asintótica de la función de error es notablemente precisa ya para pequeños $n$ Ver el diagrama de abajo para $n=3$ y $n=4$ . Para los más grandes $n$ las curvas exactas y asintóticas son indistinguibles en la escala de la figura.

---

El resultado final.

Me parece que el finito- $n$ análisis cerca de $\delta=0$ y $\delta=1/2$ junto con el gran $n$ asintótica para todo el intervalo $\delta\in(0,1/2)$ , se acerca mucho a la prueba del aumento monótono con $n$ de $P_n(\delta)$ aunque se necesita alguna estimación adicional del error en la asintótica para completar la prueba. Me sorprende el hecho de que la gran $n$ asintótica es tan precisa ya para $n=4$ .