La 'ley del seno y coseno' - fórmulas para la suma y la diferencia

Question

He leído en algún lugar que las funciones seno y coseno pueden ser completamente descritas por este teorema:

1. $\sin(0) = 0, \cos(0) = 1$
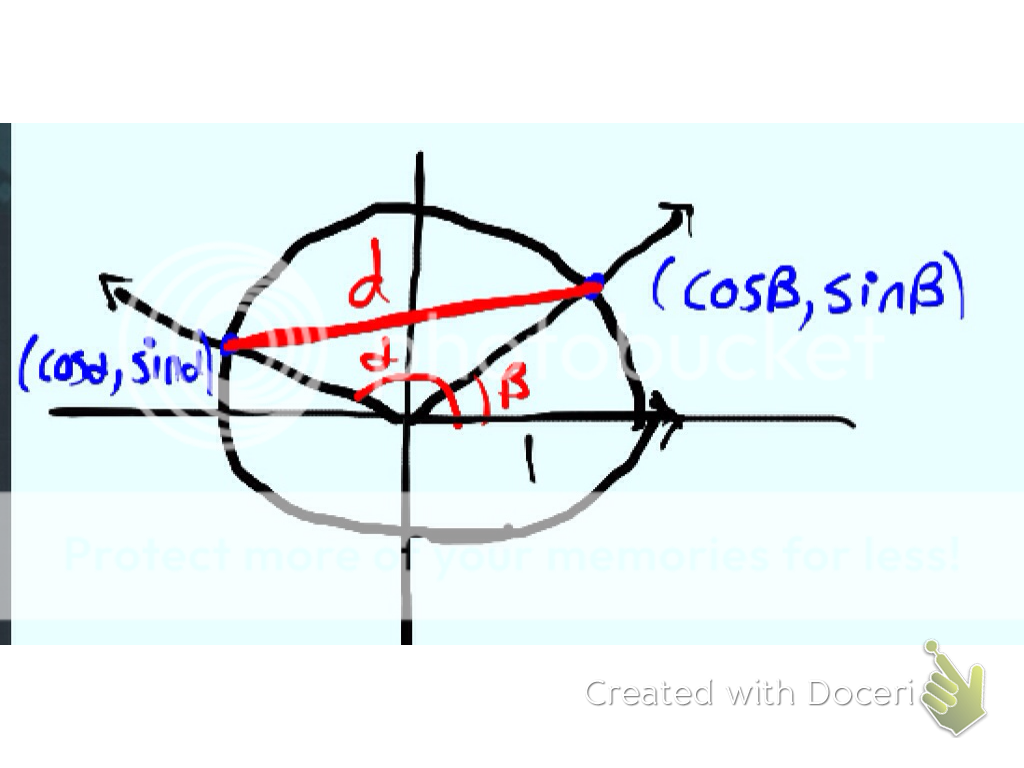
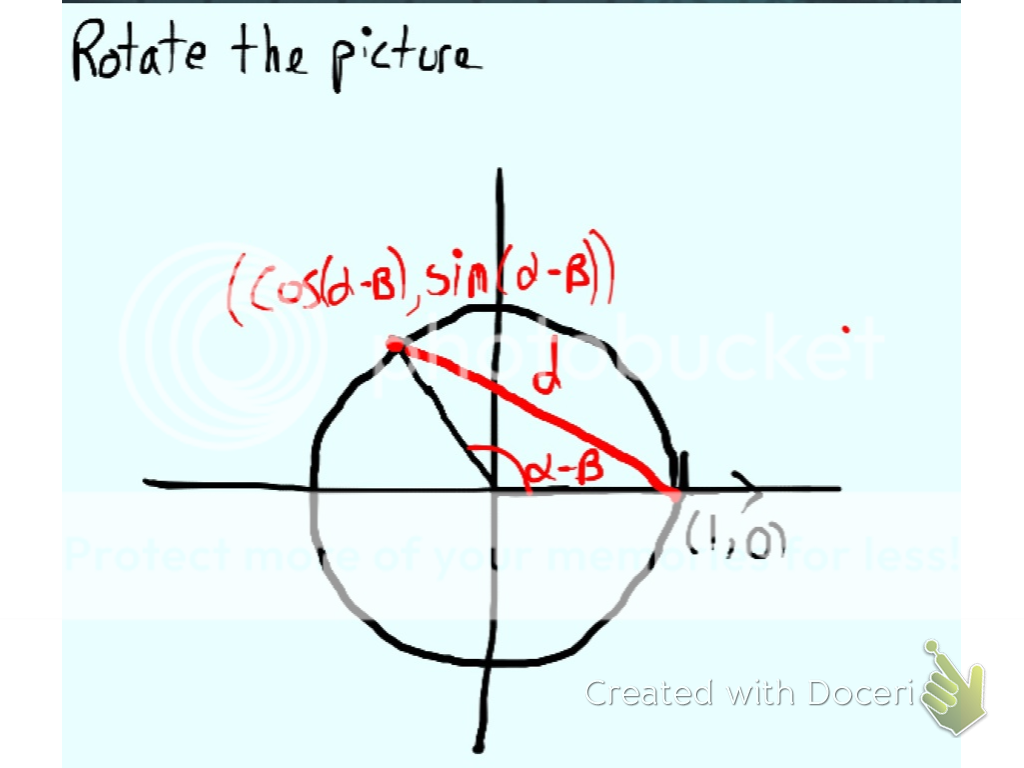
2. $\sin(a-b) = \sin(a)\cos(b) - \sin(b)\cos(a)$
3. $\cos(a-b) = \cos(a)\cos(b) + \sin(a)\sin(b)$
4. Existe un $r>0$ tal que: $$0<\sin(x)

Con este teorema, podemos demostrar cosas como:

• $\sin^2(x) + \cos^2(x) = 1$ haciendo $\cos(a-a) = \cos(a)\cos(a) + \sin(a)\sin(a)$

• $\sin(-x) = -\sin(x)$ haciendo $\sin(0-x) = \sin(0)\cos(x) - \sin(x)\cos(0)$

• $\cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b)$

  haciendo

  $\cos(a-(-b)) = \cos(a)\cos(-b) + \sin(a)\sin(-b)$

• $\sin(a+b) = \sin(a)\cos(b)+\sin(b)\cos(a)$

  haciendo

  $\sin(a-(-b)) = \sin(a)\cos(-b) - \sin(-b)\cos(a)$

Y otras identidades trigonométricas que también se derivan de lo que ya he hecho.

El problema es que hay muchas definiciones para las funciones seno y coseno. Empecemos por la definición clásica:

Definición Clásica

La función seno se define como la razón entre el lado opuesto del ángulo y la hipotenusa de este triángulo rectángulo.

La función coseno se define como la razón entre el lado adyacente del ángulo y la hipotenusa de este triángulo rectángulo.

La función tangente se define como la razón entre la función seno y la función coseno (con $\cos (x) \neq 0)$

Las otras identidades trigonométricas se pueden demostrar geométricamente para un ángulo menor o igual a $\frac{\pi}{2} \, rad$ porque es un triángulo rectángulo. Por lo tanto, no podemos demostrar $\sin(a-b)$ geométricamente y luego probar $\sin(a+b)$ analíticamente como hice, porque estamos asumiendo un $b$ negativo, algo que no está definido geométricamente en el triángulo rectángulo.

La identidad $\sin^2(x) + \cos^2(x) = 1$ se puede demostrar con un simple teorema de Pitágoras en un triángulo con una hipotenusa de 1.

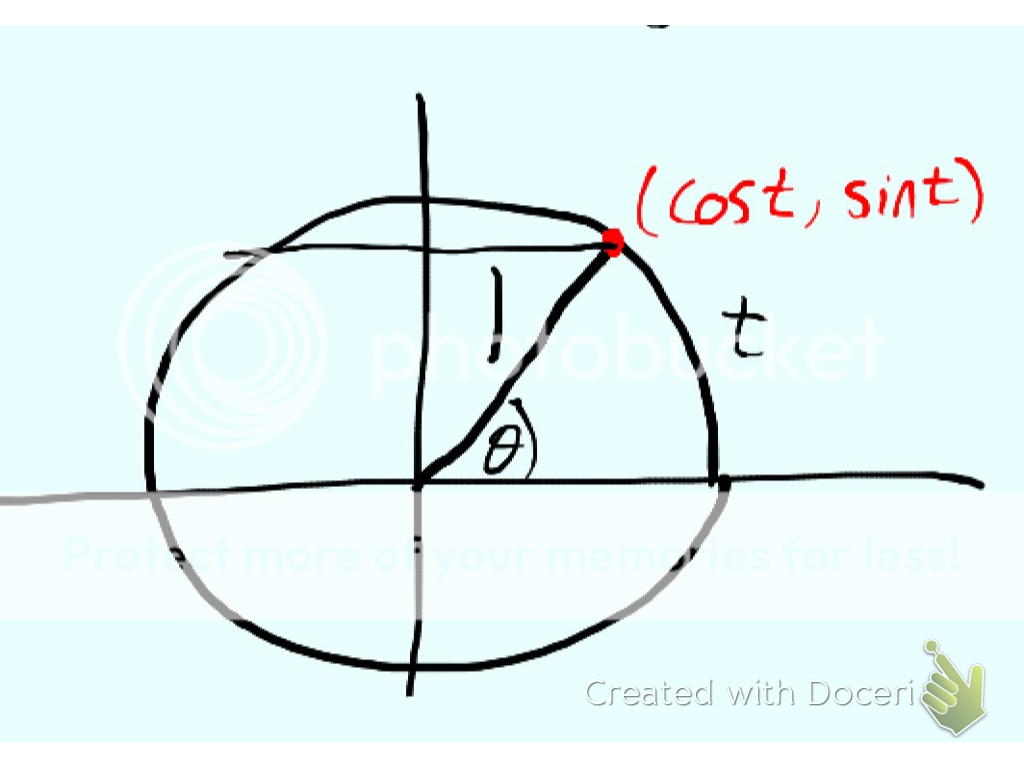
Las fórmulas para la suma y diferencia de senos y cosenos se pueden demostrar geométricamente como en estas imágenes que encontré en esta respuesta:

Definición del círculo unitario

Imagina un círculo centrado en el origen del plano cartesiano, entonces:

La función seno para un $x \in R, x>0$ se puede definir como la posición $y$ del punto del círculo donde se detiene el ángulo si viajamos en sentido antihorario dentro de la línea del círculo.

El coseno para un $x \in R, x>0$ se puede definir como la posición $x$ del punto del círculo donde se detiene el ángulo si viajamos en sentido antihorario dentro de la línea del círculo.

Podemos hacer la misma definición para los ángulos negativos, por lo que para un $x \in R, x<0$ se aplica lo mismo, pero ahora viajamos en sentido horario.

La función tangente se define como la razón entre la función seno y la función coseno (con $\cos (x) \neq 0)$

Luego, podemos definir estas funciones para todos los números reales, ya que al viajar $2\pi$ llegamos de nuevo al punto inicial. Así que definimos el seno y el coseno como funciones periódicas.

Pregunta abierta: ¿Cómo puedo probar, con la definición periódica del círculo unitario y sin ser circular, las fórmulas $\sin(a-b)$ y $\cos(a-b)$? (lo mismo para $\sin(a+b)$ y $\cos(a+b)$.

Definición de la serie de Taylor

$$\sin x = \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}$$ $$\cos x = \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n}$$ $$\tan x = \sum^{\infty}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1}$$

Aquí, en la misma pregunta, hay una prueba analítica de las identidades trigonométricas, para estas sumas.

¿Cuál es la mejor definición para el cálculo?

Bueno, en cálculo usamos las funciones trigonométricas un MONTÓN: en sustituciones integrales, en series, series de Taylor (como las que acabo de mostrar), derivadas, pruebas de convergencia (como la de Euler en el problema de Basel) y otras cosas...

Todas las definiciones que veo son un poco circulares o no lo suficientemente rigurosas como para hacerme sentir seguro al tomar algunas derivadas o sustituciones integrales, porque siempre me preocupo por el dominio de estas cosas. Así que quiero definirlo de una manera muy clara y poder usar todas las identidades trigonométricas.

He visto muchas pruebas geométricas de $\sin(a-b)$, $\sin(a+b)$, $\cos(a-b)$, $\cos(a+b)$ usando un triángulo rectángulo y luego de repente la persona comienza a usar esta fórmula para todos los números reales. Necesito una definición completa de las funciones trigonométricas que funcione de manera periódica y para todos los reales. La definición de la serie de Taylor parece buena, pero se generan usando identidades trigonométricas que aún no están demostradas (asumiendo esta definición).

pd: Sé que usé algunas palabras primitivas en algunas definiciones, como 'viajar' así que las dejé en énfasis, pero espero que lo entiendan. Y lamento la larga publicación, pero necesitaba hacerlo, porque nunca he visto una definición completa en ningún libro. Gracias.

Answer 1

La definición estándar de las funciones trigonométricas se da en términos de un círculo unitario. La definición clásica en términos de triángulos rectángulos es más limitada en cuanto a alcance. Por esta razón, en Cálculo se utiliza la definición más sólida en términos del círculo unitario. A partir de esta definición 'estándar' se pueden demostrar todas las identidades sobre las funciones trigonométricas.

En tu publicación anterior diste la definición en términos del círculo unitario, pero dejaste lo que creo que es un punto importante. Cuando se definen en términos del círculo unitario, las funciones trigonométricas son 'de valores reales'. Lo que queremos decir aquí es que se definen en términos de una distancia y no de una idea construida llamada ángulo. Así que comencemos con la definición en términos del círculo unitario, luego pasaremos a la prueba hermana de la que se dio anteriormente para el seno de una diferencia. A partir de esto, podemos establecer las otras tres identidades.

Considera el círculo unitario $$ \begin{equation}x^2+y^2 = 1 \end{equation} $$ Comenzando en el punto de intersección x (1,0) viajamos una distancia t alrededor del círculo en dirección contraria a las agujas del reloj (un movimiento en sentido horario se asignaría un signo negativo). Una vez que viajamos una distancia t alrededor del círculo, terminamos en un punto P(x,y) en el círculo. Luego definimos $$ \begin{eqnarray} \cos t = x \\ \sin t = y \end{eqnarray} $$

Luego resulta que podemos volver a los ángulos al notar que en el círculo unitario la medida en radianes del ángulo central subtiende por el arco de longitud t es igual a t. Pero no necesitamos volver a los ángulos en realidad. Nuestra definición se mantiene por sí misma. Ahora, una consecuencia inmediata de nuestra definición es la conocida identidad pitagórica para el seno y el coseno.
$$\begin{equation} \cos^2 t + \sin^2 t = 1 \end{equation} $$
(Esto se obtiene sustituyendo seno y coseno en la ecuación del círculo unitario para x e y.)

Antes de pasar a la identidad sobre la que preguntaste primero, notemos que las funciones seno y coseno son periódicas. Es decir, $$ \cos(a + 2k \pi) = \cos a $$. Creo que esto es bastante claro porque cualquier recorrido alrededor del círculo te devolverá al punto de partida. Haz ese recorrido k veces y aún estarás de regreso donde comenzaste. Por esta razón, como se mencionó anteriormente, podemos asumir que ambos ángulos están en$$ [0, 2 \pi)$$. También nota que $$\cos (-t) = \cos t $$ para todos los números reales t.

Lo último que queda por abordar es que la rotación es una transformación rígida. En otras palabras, cuando rotamos el plano alrededor de un punto, la distancia entre dos puntos antes de la rotación es la misma después de la rotación.

Ahora volvamos al problema. Muestra que
$$\cos(a-b) = \cos a \cos b + \sin a \sin b $$
Sin pérdida de generalidad, asumamos $$0

Ahora consideramos los puntos (ver diagramas) P($\cos a, \sin b)$ y Q($\cos b, \sin b)$ en el círculo unitario. Podemos usar la fórmula de distancia para encontrar la longitud del segmento PQ. Luego rotamos todo el plano en sentido horario a través de una distancia b a lo largo de la circunferencia del círculo (o a través de un ángulo con medida en radianes de b). Esto colocará el punto Q en Q`(1,0) y P estará ahora a una distancia b-a a lo largo del círculo desde (1,0) por lo que estará en P`($\cos(a-b), \sin(a-b))$. Luego procedemos a usar la fórmula de distancia. Dado que la distancia se conserva a través de la rotación, el segmento PQ y el segmento P`Q` tendrán la misma longitud.

$$\begin{eqnarray} \sqrt{(\cos a - \cos b)^2 + (\sin a - \sin b)^2} = \sqrt{(\cos(a-b)-1)^2 + (\sin(a-b) - 0)^2} \\ \cos^2 a - 2 \cos a \cos b + \cos^2 b + \sin^2 a - 2 \sin a \sin b + \sin^2 b = \cos^2(a-b) - 2 \cos(a-b) + 1 + \sin^2(a-b) \\ \cos^2 a + \sin^2 a + \cos^2 b + \sin^2 b - 2 \cos a \cos b - 2 \sin a \sin b = \cos^2(a-b) + \sin^2(a-b) + 1 - 2 \cos(a-b) \\ - 2 \cos a \cos b - 2 \sin a \sin b = - 2 \cos(a-b) \\ \cos a \cos b \sin a \sin b = \cos(a-b) \end{eqnarray} $$

¿Ahora asumí $b

Armados con la fórmula del coseno de la diferencia, ahora podemos demostrar lo siguiente.

$$ \begin{eqnarray} \cos(a+b) = \cos(a-(-b)) = \cos a \cos(-b) - \sin a \sin(-b) \\ = \cos a \cos b - \sin a \sin b \end{eqnarray} $$

El último paso en la igualdad proviene de nuestra identidad para $\cos(-t)$ anterior y el hecho de que $\sin(-t) = -\sin(t) $ como se mencionó en la publicación anterior.

Ahora podemos mostrar que $\cos(\frac{\pi}{2} - x) = \sin x$ y de manera similar al problema anterior que $\sin(\frac{\pi}{2} - x) = cos x$. Estas son tus conocidas identidades de cofunción. Finalmente, armados con estas ecuaciones, ahora podemos demostrar el seno de una diferencia que luego puede probar la fórmula del seno de una suma.

$$ \begin{eqnarray} \sin(a-b) = \cos(\frac{\pi}{2} - (a-b)) \\ = \cos((\frac{\pi}{2} -a) + b) \\ = \cos(\frac{\pi}{2} -a) \cos b - \sin(\frac{\pi}{2} -a) \sin b \\ = \sin a \cos b - \cos a \sin b \end{eqnarray} $$

Y ahí lo tenemos. Pido disculpas si la formatación está un poco desordenada, todavía me estoy acostumbrando al sistema. Pero ahora, a partir de estas identidades, puedes demostrar la mayoría de las otras identidades básicas que involucran las funciones trigonométricas. Todas tus fórmulas de ángulo doble y medio, y tus fórmulas de suma-producto y producto-suma.

Answer 2

I. Creo que, en el punto en el que te encuentras, estarás más satisfecho al principio con un desarrollo de la teoría de las funciones trigonométricas que comience con consideraciones geométricas y se construya a partir de ahí. Para esto conozco dos enfoques:

Primero, puedes empezar con ratios de lados en triángulos rectángulos, definiendo las funciones primero para ángulos agudos y luego extendiéndolas cuidadosamente a dominios más grandes. El único lugar donde he visto que esto se haga en detalle es en el pequeño libro Trigonometry, de Gelfand y Saul, que recomiendo encarecidamente (aunque es un libro de texto para niños). Una característica muy buena es que dan las razones correctas para elegir las extensiones que hacen, por ejemplo, justifican la extensión del seno de $[0^\circ,90^\circ]$ a $[0^\circ,180^\circ]$ observando que es la única manera de que la ley de los senos sea correcta también para triángulos obtusos. La ley aditiva es el teorema de Ptolomeo, para cierto rango de ángulos, y luego las extensiones se eligen para que sea válida en todas partes.

Alternativamente, puedes derivar una fórmula integral para el área de un sector circular, y luego usar esa función para definir el seno y el coseno. Esto se hace cuidadosamente en el capítulo 15 del Cálculo de Spivak.

II. Ahora, una vez que tengas todo en una base sólida como esa, puedes renovar: elegir alguna propiedad probada del seno y/o coseno que determine por completo esas funciones, tomarla como una nueva definición de esas funciones, y reconstruir la teoría sobre esa base. Por supuesto, esto solo tiene sentido cuando ya sabes que las funciones en las que estás interesado tienen esas propiedades (porque lo probaste a partir de la antigua definición), de lo contrario te quedarás preguntándote cómo sabemos que estas funciones recién definidas son las mismas que las que ya conocíamos, pero internamente se sostiene por su propia lógica. A veces este tipo de renovación puede hacer que la teoría sea más elegante, a veces permite el uso de las funciones en un nuevo contexto donde la antigua definición es insensata, a veces simplemente es novedoso. Aquí hay algunas propiedades de este tipo:

Primero, el seno es la única función $f$ que satisface

• $f''=-f$
• $f(0)=0$
• $f'(0)=1$

(Ver Teorema 4 de Spivak. Demuestra la ley aditiva no a partir de su definición, sino a partir de estas propiedades, de manera bastante ordenada. Se podría ver su definición como simplemente un asunto técnico de mostrar que alguna función que tenga estas propiedades existe, lo cual también se podría manejar con la teoría de las ecuaciones diferenciales.)

Segundo, puedes definir el seno y el coseno por sus series de potencias. Este es un enfoque muy bueno si los vas a usar con números complejos.

Tercero, $$ \sin x = \frac{e^{ix} - e^{-ix}}{2i} $$ así que si has definido de alguna manera el exponencial complejo, puedes obtener las funciones trigonométricas. (Por supuesto, definir el exponencial complejo implica consideraciones mucho más complicadas.)

Cuarto, dado un número real positivo $p$, existe exactamente un par de funciones $S,C$ que satisfacen

• $C(x-y)=C(x)C(y)+S(x)S(y)$
• $S(p)=1$
• $S(x)\ge 0$ para todo $x\in [0,p]$.

Este es el resultado principal de G. B. Robison, "A New Approach to Circular Functions, $\pi$ and $\lim (\sin x)/x$", Math. Mag. 41 (1968), 66–70 (jstor). Tomar $p=\frac\pi2$ produce las funciones seno y coseno usuales. (De hecho, el autor sugiere primero tomar $S$ y $C$ como las funciones obtenidas con $p=1$, y luego definir $\pi = 2\lim_{x\to 0} S(x)/x$.) El artículo demuestra todas las identidades trigonométricas básicas habituales en el camino, excepto, por supuesto, la identidad para $\cos(x-y)$, ¡ya que esa es la definición!

Robison hace referencia a un artículo ligeramente anterior (W. F. Eberlein, "The Circular Function(s)", Math. Mag. 39 (1966), 197–201) que básicamente define primero la arcotangente (por una integral, como se sugiere en comentarios), luego la usa para definir la función que normalmente se escribiría como $x\mapsto e^{ix}$, y luego el seno y coseno.

III. Preguntaste específicamente cómo probar las fórmulas de adición a partir de la definición del círculo unitario. Mi método favorito (aunque no del todo riguroso) es este: la definición del círculo unitario consiste en decir que si $R_\theta$ denota una rotación en sentido antihorario alrededor del origen por $\theta$ radianes entonces $$ R_\theta\left[\begin{matrix} 1 \\ 0 \end{matrix}\right] = \left[\begin{matrix} \cos\theta \\ \sin\theta \end{matrix}\right] $$ Con un poco de geometría puedes mostrar también que $$ R_\theta\left[\begin{matrix} 0 \\ 1 \end{matrix}\right] = \left[\begin{matrix} -\sin\theta \\ \phantom-\cos\theta \end{matrix}\right] $$ Puedes demostrar que $R_\theta$ es lineal (digamos, porque es una isometría que fija el origen). Así que tiene una matriz, y las dos declaraciones anteriores muestran que esta matriz es $$ \left[\begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \phantom-\cos\theta \end{matrix}\right] $$ Ahora, es intuitivamente obvio que $R_{a+b}=R_a\circ R_b$; por lo tanto $$ \left[\begin{matrix} \cos (a+b) & -\sin (a+b) \\ \sin (a+b) & \phantom-\cos (a+b) \end{matrix}\right] = \left[\begin{matrix} \cos a & -\sin a \\ \sin a & \phantom-\cos a \end{matrix}\right] \left[\begin{matrix} \cos b & -\sin b \\ \sin b & \phantom-\cos b \end{matrix}\right] $$ Multiplicar las matrices en el RHS e identificar las entradas correspondientes te da las fórmulas de adición. [Editar: Y, por supuesto, esto está en la pregunta vinculada.]

Answer 3

Mi recuerdo del cálculo de la escuela secundaria es que para el cálculo, dependíamos de la definición del círculo unitario, que coincide con la definición clásica de seno y coseno para ángulos en el rango $[0, \pi/2]$ siempre y cuando aceptes que la medida del ángulo es igual a la longitud del arco interceptado.

En el círculo unitario, al recorrer una distancia de $2\pi$ regresas al punto de partida, por lo que puedes demostrar que si $\sin \theta = y$, entonces $\sin (\theta + 2n\pi) = y$ para cualquier entero $n$. Luego puedes mostrar mediante triángulos congruentes (reflejados a través del eje $x$) que $\sin(-x) = -\sin x$ para cualquier número real $x$.

Entonces, sin pérdida de generalidad, al evaluar $\sin(a - b)$ podemos asumir que $-\pi < a - b \le \pi$. Podemos resolver fácilmente los casos $a - b = 0$ y $a - b = \pi$. Además, siempre que $-\pi < a - b < 0$, podemos utilizar el hecho de que $\sin(a - b) = -\sin(b - a)$, por lo que realmente solo necesitamos encontrar la fórmula para $\sin(a - b)$ en el caso donde $0 < a - b < \pi$.

Sea $O$ el centro del círculo, $A$ el punto al que llegas después de recorrer la distancia $a$ en sentido antihorario en el círculo, y $B$ el punto al que llegas después de recorrer la distancia $b$. Entonces, $\triangle AOB$ es un triángulo cuyo ángulo en $O$ es $a - b$. Ahora aplicamos la siguiente transformación a las coordenadas $x$ y $y$ de $A$ y $B$:

\begin{eqnarray} x \rightarrow x \cos b + y \sin b, \\ y \rightarrow y \cos b - x \sin b. \end{eqnarray}

Sean $A'$ y $B'$ los puntos cuyas coordenadas se obtienen aplicando esta transformación a las coordenadas de $A$ y $B$, respectivamente. Dado que las coordenadas de $B$ son $(\cos b, \sin b)$, podemos mostrar que las coordenadas de $B'$ son $(1, 0)$. Podemos usar la fórmula de Pitágoras en pares de coordenadas para demostrar que la distancia de $O = (0,0)$ a $A'$ es $1$, y que la distancia de $A'$ a $B'$ es igual a la distancia de $A$ a $B$, y ahora sabemos que los triángulos $\triangle AOB$ y $\triangle A'OB'$ son congruentes. Por lo tanto, el ángulo en $O$ en $\triangle A'OB'$ tiene medida $a - b$. Mientras tanto, podemos encontrar que la coordenada $y$ de $A'$ es $\sin a \cos b - \cos a \sin b$. Solo queda mostrar que $\triangle AOB$ y $\triangle A'OB'$ tienen la misma orientación (de modo que $A'$ esté por encima del eje $x$), lo cual puedes hacer aplicando una fórmula sobre las coordenadas de los vértices de un triángulo que da la orientación del triángulo (es decir, el resultado se multiplica por $-1$ si reflejas el triángulo), o mediante otro conocimiento de isometrías. Una vez que sepamos esto, hemos demostrado que

\begin{equation} \sin(a - b) = \sin a \cos b - \cos a \sin b. \end{equation}

Un procedimiento similar funciona para la fórmula de diferencia de cosenos, aunque en este caso no tenemos que mostrar que $A'$ esté por encima del eje:

\begin{equation} \cos(a - b) = \cos a \cos b - \sin a \sin b. \end{equation}

Para $\sin(a + b)$ y $\cos(a + b)$, simplemente sustituye $-b$ por $b$ en las fórmulas ya conocidas.

Answer 4

Creé esta prueba de atajo para la fórmula de adición del coseno, utiliza las fórmulas del coseno y seno. La demostración que conozco generalmente implica formas de triángulos complejos, así que trabajaré con un triángulo básico aquí

$a+b+c = \pi$, y $c = \pi -(a+b)$ $$ C^2 = A^2+B^2-2AB\cos{c}$$ $$ C^2 = A^2+B^2-2AB\cos{(\pi-(a+b))}$$ $$\frac{C^2}{A^2} = \frac{A^2}{A^2}+\frac{B^2}{A^2}-2\frac{AB}{A^2}\cos{(\pi-(a+b))}$$ $${\frac{C}{A}}^2 = 1+{\frac{B}{A}}^2-2\frac{B}{A}\cos{(\pi-(a+b))}$$ $$\frac{\sin{a}}{A} = \frac{\sin{b}}{B} = \frac{\sin{c}}{C} $$ $$\frac{\sin^2{c}}{\sin^2{a}} = 1+\frac{\sin^2{b}}{\sin^2{a}}-2\frac{\sin{b}}{\sin{a}}\cos{(\pi-(a+b))}$$ $$\sin^2{c} = \sin^2{a} \cdot ( 1+\frac{\sin^2{b}}{\sin^2{a}}-2\frac{\sin{b}}{\sin{a}}\cos{(\pi-(a+b))} )$$ $$1-\sin^2{c} = 1-\sin^2{a} \cdot ( 1+\frac{\sin^2{b}}{\sin^2{a}}-2\frac{\sin{b}}{\sin{a}}\cos{(\pi-(a+b))} )$$ $$\cos^2{c} = 1-\sin^2{a} \cdot ( 1+\frac{\sin^2{b}}{\sin^2{a}}-2\frac{\sin{b}}{\sin{a}}\cos{(\pi-(a+b))} )$$ $$\cos^2{c} = 1-\sin^2{a}-\sin^2{b}+2\sin{a}\sin{b}\cos{c}$$ $$\cos^2{c} - 2\sin{a}\sin{b}\cos{c}+\sin^2{a}+\sin^2{b}-1 = 0$$ $$\cos{c} = \frac{ 2\sin{a}\sin{b} \pm \sqrt{ (2\sin{a}\sin{b})^2-4(\sin^2{a}+\sin^2{b}-1) } }{2}$$ $$\cos{c} = \frac{ 2\sin{a}\sin{b} \pm \sqrt{ 4\sin^2{a}\sin^2{b}-4\sin^2{a}-4\sin^2{b}+4 } }{2}$$ $$\cos{c} = \frac{ 2\sin{a}\sin{b} \pm 2\sqrt{ \sin^2{a}\sin^2{b}-\sin^2{a}-\sin^2{b}+1 } }{2}$$ $$\cos{c} = \frac{ 2\sin{a}\sin{b} \pm 2\sqrt{ (1-\sin^2{a})(1-\sin^2{b}) } }{2}$$ $$\cos{c} = \frac{ 2\sin{a}\sin{b} \pm 2\sqrt{ \cos^2{a}\cos^2{b} } }{2}$$ $$\cos{c} = \sin{a}\sin{b} \pm \cos{a}\cos{b}$$ $$\cos{(\pi-(a+b))} = \sin{a}\sin{b} - \cos{a}\cos{b}$$ $$-\cos{(a+b)} = \sin{a}\sin{b} - \cos{a}\cos{b}$$ $$\cos{(a+b)} = \cos{a}\cos{b}- \sin{a}\sin{b}$$

Answer 5

La definición más directa es de $e^z$.

Primero define $e^z = \sum_{k=0}^\infty \frac{z^n}{n!}$, y demuestra que $e^{z+z'}=e^ze^{z'}$ usando un producto de Cauchy. También obtienes de inmediato que la derivada de $e^z$ es $e^z$.

Define $\cos z = \frac{e^{iz}+e^{-iz}}{2}$, $\sin z = \frac{e^{iz}-e^{-iz}}{2i}$, y de manera similar $\cosh z = \frac{e^{z}+e^{-z}}{2}$, $\sinh z = \frac{e^{z}-e^{-z}}{2}$. Tendrás trivialmente las derivadas de estas funciones. Como observación adicional, esto elimina el problema habitual con $\lim_{x\rightarrow 0} \frac{\sin x}{x}=1$, al definir las funciones trigonométricas geométricamente.

A partir de la fórmula $e^{z+z'}=e^ze^{z'}$, puedes derivar la mayoría de las fórmulas trigonométricas habituales (excepto aquellas que involucran $\pi$, que aún está por definirse). Obtiene casi las mismas fórmulas para la trigonometría hiperbólica.

Observa que $\cos z$ y $\sin z$ son valores reales para $z$ real. A partir de la definición de la serie, sabes que son $C^\infty$ en $\Bbb R$, y especialmente, son continuas. Tienes $\cos 0 = 1$ y es fácil de probar que $\cos 2<0$, por lo tanto, $\cos$ tiene una raíz en $]0, 2[$. De manera similar, puedes probar que $\sin x > 0$ en este intervalo, y a partir de $\cos'=-\sin$, sabes que $\cos$ tiene solo una raíz. Llámala $\frac{\pi}{2}$ (es decir, define $\pi$ como dos veces la raíz). Luego, a partir de las fórmulas de adición, es fácil probar que $\cos$ y $\sin$ son periódicas con $2\pi$.

Entonces ya tienes las propiedades principales de estas funciones. Si lo deseas, también puedes definir $\tan x$ y todas las demás funciones menos conocidas (secante, cosecante, cotangente), y derivar fórmulas para $\tan (x+y)$ y similares. Y definir funciones trigonométricas inversas (bueno, estrictamente hablando, son inversas de restricciones de funciones trigonométricas a intervalos cuidadosamente elegidos, para que sean biyectivas en ellos), etc.