Digamos que tenemos un icosaedro regular, construido enteramente con triángulos equiláteros:
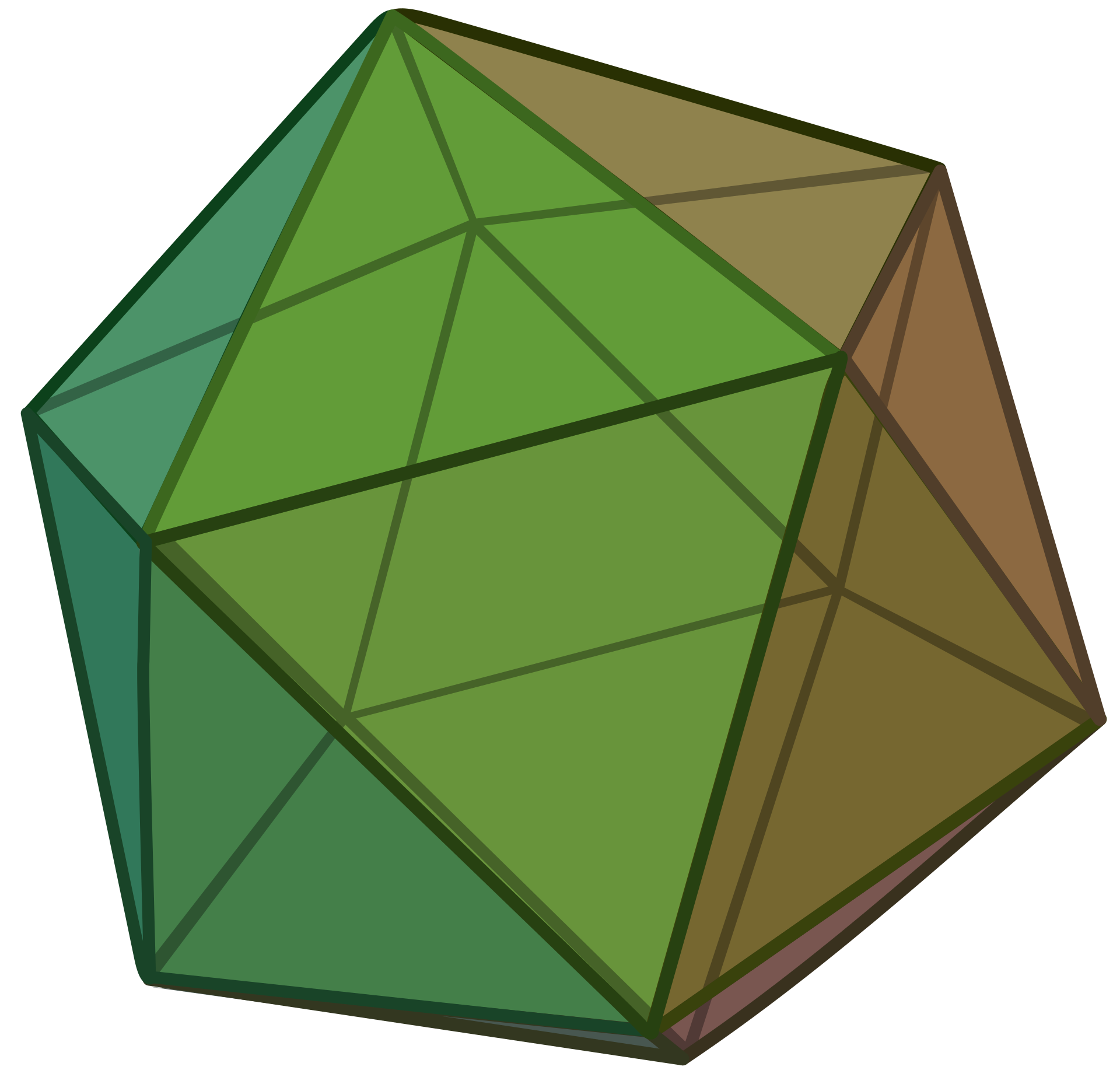
Si se "aplanara" un vértice de la estrella de ese Icosaedro, se tendría una estrella con cinco líneas que salen de ella, así: 
Para conseguir aplanar este trozo de icosaedro, hay que hacer dos concesiones, el ángulo entre las líneas pasa de 60° a 72°, y la línea más externa de cada triángulo equilátero debe "crecer" de 100 a ~117,557.
Puedo calcular bien todas las piezas de ese triángulo, y aquí: 
Lo que tengo que averiguar es a qué ángulo tengo que elevar cada línea para que el ángulo interior vuelva a ser de 60º. Para entender lo que quiero decir, veamos una esfera unitaria en referencia a dos de las líneas de nuestro Icosaedro: [![introduce aquí la descripción de la imagen][5]] El dibujo de la izquierda muestra que a 90° (completamente horizontal) estamos en el ángulo de 72°, pero al subirlas (igualmente, juntas) llegarán a 60°. A la izquierda estamos en el "máximo" de la anchura de las rodajas de naranja. A medida que vayamos subiendo (o bajando) eso irá disminuyendo, y en algún momento volverá a los 60°, que es el ángulo que necesitamos para que el Icosaedro vuelva a su forma correcta.
Según entiendo, a medida que las dos líneas alcanzan un desplazamiento de 90° respecto a la horizontal, se acercan (y luego llegan) a 0. Esto es alguna función de SIN(), ya que ésta va de 1 a 0 en esta dirección. Tengo una comprensión bastante buena de cómo descomponer todos estos problemas cuando se separan en sus componentes bidimensionales, pero no sé cómo derivar una ecuación que relaciona las diversas perspectivas juntas. ¿De qué manera afecta el ángulo ascendente de cada línea al ángulo interior entre las líneas?
Actualización: Bien, he encontrado una manera de encontrar la respuesta, pero es a través de medios "no convencionales". Utilicé Fusion 360 para producir la rebanada de naranja con los parámetros que he estado utilizando. A continuación, esbocé un rectángulo de 100 unidades en ángulo y por encima de la rebanada de tal manera que cuando lo usé para cortar la rebanada, revelaría dos puntos de "colmillo" en los que estaban los incidentes de intersección donde la distancia entre los dos puntos era la longitud exacta del rectángulo. Entonces medí el ángulo entre el punto y la horizontal: 
Por lo tanto, la respuesta directa a la pregunta es 31,717 grados ... pero aún no sé cómo resolver esto sin usar Fusion 360 y hackear la geometría.


