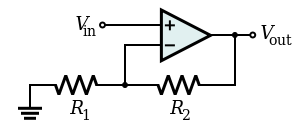
Para derivar esto correctamente a partir de los principios básicos, hay que trabajar con la ganancia de bucle abierto del amplificador. Parece que estás confundiendo la ganancia en bucle abierto y en bucle cerrado, o quizás no has entendido cómo funcionan los op-amps. La tensión de salida no es la diferencia entre + y -. Es la diferencia entre + y - multiplicada por la ganancia en bucle abierto.
En las configuraciones de amplificación de los op-amps, la diferencia entre + y - es siempre muy pequeña. Fracciones de un milivoltio. Es tan pequeña, que podemos entender muchos circuitos con la útil suposición simplificadora de que la tensión es la misma en + y -. Esta pequeñísima diferencia de tensión entre + y - se multiplica por el enorme ganancia en bucle abierto para producir la salida. Es la retroalimentación la que calibra esta diminuta tensión diferencial para que se obtenga una tensión de salida razonable a pesar de la enorme ganancia.
Así pues, definamos algunas variables:
$$A_0 = open\ loop\ gain$$ $$V_+ = voltage\ at\ +\ terminal$$ $$V_- = voltage\ at\ -\ terminal$$ $$V_{out} = output\ voltage$$
Ahora, tenemos:
$$V_{out} = A_o (V_+ - V_-)$$
Pero, como tenemos un camino de retroalimentación, el voltaje en el terminal - es establecido por el voltaje de salida por el divisor de voltaje:
$$V_- = {R1\over{R1 + R2}} V_{out}$$
Para simplificar, reduzcamos esta fracción formada por las resistencias a una sola variable que llamamos f, por retroalimentación:
$$f = {R1\over{R1 + R2}}$$ $$V_- = f V_{out}$$
Así que ahora podemos sustituir este V- en la primera fórmula:
$$V_{out} = A_o (V_+ - f V_{out})$$
La tensión de salida es la tensión V+, menos la tensión de retroalimentación, escalada por la ganancia de lazo abierto. Factorizamos la Ao y luego obtenemos los términos de Vout juntos:
$$V_{out} = A_oV_+ - fA_oV_{out}$$
$$V_{out} + fA_oV_{out} = A_oV_+$$
$$V_{out} (1 + fA_o) = A_oV_+$$
$$V_{out} = {A_oV_+\over 1 + fA_o}$$
Ahora el siguiente paso requiere que hagamos una suposición: la ganancia en lazo abierto del amplificador Ao es muy grande, como 100.000 o más. Lo que esto significa es que el 1 + en la parte inferior no hace ninguna diferencia, porque fAo es un número grande (a menos que f sea un número muy pequeño, pero sólo estamos interesados en el uso de retroalimentación significativa, en lugar de retroalimentación insignificante). Así que lo que hacemos es simplemente eliminar el uno:
$$V_{out} = {A_oV_+\over fA_o}$$
Ahora la ganancia de bucle abierto en la parte superior e inferior se cancela, dejándonos con:
$$V_{out} = {V_+\over f}$$
La tensión de salida es la tensión de entrada dividida por la realimentación. Si la retroalimentación es 1/5, la tensión de salida es cinco veces la tensión de entrada, etc. Ahora un paso más: sustituir la fracción de la resistencia por f:
$$V_{out} = {V_+\over {R1\over{R1 + R2}}}$$
$$V_{out} = {{R1 + R2\over R1}}V_+$$
Y por supuesto
$${{R1 + R2\over R1}} = 1 + {R2\over R1}$$
que es lo que estás buscando.
No olvides nunca que esta sencilla fórmula que relaciona la tensión de entrada y la de salida sólo funciona porque tanto la realimentación como la ganancia de bucle abierto son tan grandes que somos capaces de ignorar el 1 en 1 + fA0. Esta suposición puede romperse. Por ejemplo, a frecuencias cada vez más altas, los op-amps tienen cada vez menos ganancia de bucle abierto. A cierta frecuencia, la ganancia de bucle abierto cae hasta 1, y luego cae un poco más a frecuencias aún más altas.